《电路》课程教学资源（A）习题解答_第3章 电阻电路的一般分析

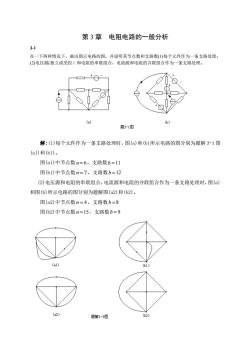
第3章电阻电路的一般分析 3-1 在一下两种情况下，画出图示电路的图，并说明其节点数和支路数(1)每个元件作为一条支路处理： (2)电压源（独立或受控）和电阻的串联组合，电流源和电阻的并联组合作为一条支路处理。 (a) 6) 题31图 解：(1)每个元件作为一条支路处理时，图(a)和(b)所示电路的图分别为题解3-1图 (al)和(bl)。 图(al)中节点数n=6,支路数b=11 图(61)中节点数n=7,支路数b=12 (2)电压源和电阻的串联组合，电流源和电阻的并联组合作为一条支路处理时，图() 和图(b)所示电路的图分别为题解图(a2)和(62)。 图(a2)中节点数n=4,支路数b=8 图(b2)中节点数n=15,支路数b=9 (a1) 0b1 (a2) 题解1-3图

第 3 章 电阻电路的一般分析 3-1 在一下两种情况下，画出图示电路的图，并说明其节点数和支路数(1)每个元件作为一条支路处理； (2)电压源(独立或受控）和电阻的串联组合，电流源和电阻的并联组合作为一条支路处理。 解:(1)每个元件作为一条支路处理时，图(a)和(b)所示电路的图分别为题解 3-1 图 (a1)和(b1)。 图(a1)中节点数 n = 6 ，支路数 b =11 图(b1)中节点数 n = 7 ，支路数 b =12 (2)电压源和电阻的串联组合，电流源和电阻的并联组合作为一条支路处理时，图(a) 和图(b)所示电路的图分别为题解图(a2)和(b2)。 图(a2)中节点数 n = 4 ，支路数 b = 8 图(b2)中节点数 n =15，支路数 b = 9

3-2 指出题3-1中两种情况下，KCL,KL独立方程数各为多少？ 解：题3-1中的图(a)电路，在两种情况下，独立的KCL方程数分别为 (1)n-1=6-1=5(2)n-1=4-1=3 独立的KVL方程数分别为 (1)b-n+1=11-6+1=6(2)b-n+1=8-4+1=5 图(b)电路在两种情况下，独立的KCL方程数为 (1)n-1=7-1=6(2)n-1=5-1=4 独立的KVL方程数分别为 (1)b-n+1=12-7+1=6(2)b-n+1=9-5+1=5 对题图()和(b)所示G,各画出4个不同的树，树支数各为多少？ 3 题3-3图 解：一个连通图G的树T是这样定义的：（山）T包含G的全部结点和部分支路：(2)T本身是 连通的且又不包含回路。根据定义，画出图(a)和(b)所示图G的4个树如题解33图a)和(b)所示。树 支数为结点数减一。故图()的数有树支，图b)的树有树支 n-1=6-1=5o

3-2 指出题 3-1 中两种情况下，KCL,KVL 独立方程数各为多少？ 解：题 3－1 中的图(a)电路，在两种情况下，独立的 KCL 方程数分别为 (1) n −1= 6 −1= 5 (2) n −1= 4 −1= 3 独立的 KVL 方程数分别为 (1) b − n +1=11−6+1= 6 (2) b − n +1= 8− 4+1= 5 图(b)电路在两种情况下，独立的 KCL 方程数为 (1) n −1= 7 −1= 6 (2) n −1= 5−1= 4 独立的 KVL 方程数分别为 (1) b − n +1=12−7 +1= 6 (2) b − n +1= 9−5+1= 5 3-3 对题图(a)和(b)所示 G ，各画出 4 个不同的树，树支数各为多少？ 解：一个连通图 G 的树 T 是这样定义的：(1) T 包含 G 的全部结点和部分支路；(2) T 本身是 连通的且又不包含回路。根据定义，画出图(a)和(b)所示图 G 的 4 个树如题解 3-3 图(a)和(b)所示。树 支 数 为 结 点 数 减 一 。 故 图 (a) 的 数 有 树 支 ， 图 (b) 的 树 有 树 支 n− = − = 1 6 1 5

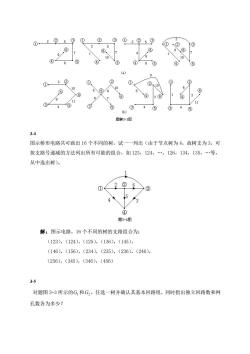
①2② 5① ③ ①2②5③ ④8 ④ ① ① 10 5④/6 5 ④ 3 /11 4⑤ ③4⑤ 题解3-3图 34 图示桥形电路共可画出16个不同的树，试一一列出（由于节点树为4，故树支为3，可 按支路号递减的方法列出所有可能的组合，如123,124，.，126,134,135，.等， 从中选出树)。 3-4图 解：图示电路，16个不同的树的支路组合为： (123),(124),(125),(136),(145), (146),(156),(234),(235),(236),(246) (256),(345),(346),(456) 35 对题图3-3所示的G,和G,任选一树并确认其基本回路组，同时指出独立回路数和网 孔数各为多少？

3-4 图示桥形电路共可画出 16 个不同的树，试一一列出（由于节点树为 4，故树支为 3，可 按支路号递减的方法列出所有可能的组合，如 123，124，.，126，134，135，.等， 从中选出树）。 解：图示电路，16 个不同的树的支路组合为： （123），（124），（125），（136），（145）， （146），（156），（234），（235），（236），（246）， （256），（345），（346），（456） 3-5 对题图 3-3 所示的 G1 和 G2 ，任选一树并确认其基本回路组，同时指出独立回路数和网 孔数各为多少？

器品o 路，是， 6,7,10,ii 题解3-5日 0) 解：在连通图G中，由树支和一个连支组成的回路称为G的基本回路（或单连支回 路)，基本回路是独立回路，网孔也是独立回路，因此，基本回路数=独立回路数十网 孔数。对一个节点数为n,支路数为b的连通网，其独立回路数1-(b-n+)。从题图 3-3所示的G,和G,中任选一树，（见题解3-5图(a)和(b)中粗线所示），对应于这一树 的基本回路分别为1=5,1，=6。 3-6 对图示非平面图，设：(1)选择支路(1,2,3,4)为树：(2)选择支路(5,6,7， 8)为树，问独立回路各有多少？求其基本回路组。 解：图中有结点数n=5,支路数b=10,故独立回路树为b-n+1=10-5+1=6 (1)选择支路(1,2,3,4)为树，对应的基本回路组为：(1,2,3,4,5)，(1， 2,3,7)(1,2,6),(2,3,4,8),(2,3,9),(3,4,10) (2)选择支路(5,6,7,8)为树，对应的基本回路组为：(1,5,8)，(2,5,6， 8),(3,6,7),(4,5,7),(5,7,8,9),(5,6,10)

解：在连通图 G 中，由树支和一个连支组成的回路称为 G 的基本回路（或单连支回 路），基本回路是独立回路，网孔也是独立回路，因此，基本回路数＝独立回路数＋网 孔数。对一个节点数为 n ，支路数为 b 的连通网，其独立回路数 l = (b − n +1) 。从题图 3-3 所示的 G1 和 G2 中任选一树，（见题解 3-5 图(a)和(b)中粗线所示），对应于这一树 的基本回路分别为 l 1 = 5,l 2 = 6。 3-6 对图示非平面图，设：（1）选择支路（1，2，3，4）为树；（2）选择支路（5，6，7， 8）为树，问独立回路各有多少？求其基本回路组。 解：图中有结点数 n = 5 ，支路数 b =10 ，故独立回路树为 b − n +1=10−5+1= 6 （1）选择支路（1，2，3，4）为树，对应的基本回路组为：（1，2，3，4，5），（1， 2，3，7），（1，2，6），（2，3，4，8），（2，3，9），（3，4，10） （2）选择支路（5，6，7，8）为树，对应的基本回路组为：（1，5，8），（2，5，6， 8），（3，6，7），（4，5，7），（5，7，8，9），（5，6，10）

3-7 图示电路中R=R=102,R,=42,R=R=82,R=22,4=20,46=40,用支 路电流法求解电流：。 R61 ①u 题3-7图 解：本题电路有4个节点，6条支路，独立回路数为6一4+1=3。设各支路电流和 独立回路绕行方向如图所示，由KCL列方程，设流出节点的电流取正号。 节点①1+12+6=0 节点② -42+1+14=0 节点③ -i4+i3-i6=0 由KVL列方程 回路1 2i。-814-102=-40 回路Ⅱ -101,+1012+43=-20 回路Ⅲ-41，+81，+81，=20 联立求解以上方程组，得电流5=0.956A 注：由本题的求解过程可以归纳出用支路电流法分析电路的步骤如下： (1)选定各支路电流的参考方向： (2)任取(-1)个结点，依KCL列独立结点电流方程： (3)选定(b+1)个独立回路（平面回路可选网孔），指定回路的绕行方向，根据KL列 写独立回路电压方程：

3-7 图示电路中 R1 = R2 =10 ,R3 = 4 ,R4 = R5 = 8 ,R6 = 2 ,us3 = 20V,us6 = 40V ，用支 路电流法求解电流 5 i 。 解：本题电路有 4 个节点，6 条支路，独立回路数为 6－4＋1=3。设各支路电流和 独立回路绕行方向如图所示，由 KCL 列方程，设流出节点的电流取正号。 节点① i 1 + i 2 + i 6 = 0 节点② − i 2 + i 3 + i 4 = 0 节点③ − i 4 + i 5 − i 6 = 0 由 KVL 列方程 回路Ⅰ 2i 6 −8i 4 −10i 2 = −40 回路Ⅱ −10i 1 +10i 2 + 4i 3 = −20 回路Ⅲ − 4i 3 + 8i 4 + 8i 5 = 20 联立求解以上方程组，得电流 i 5 = −0.956 A 注：由本题的求解过程可以归纳出用支路电流法分析电路的步骤如下： （1）选定各支路电流的参考方向； （2）任取（n-1）个结点，依 KCL 列独立结点电流方程； （3）选定（b-n+1）个独立回路（平面回路可选网孔），指定回路的绕行方向，根据 KVL 列 写独立回路电压方程；

(4)求解联立方程组，得到个支路电流， 需要明确：以上支路电流法求解电路的步骤只适用于电路中每一条支路电压都能用支路电 流表示的情况，若电路中含有独立电流源或受控电流源，因其电压不能用支路电流表示，故不能直 接使用上述步骤。此外，若电路中含有受控源，还应将控制量用支路电流表示，即要多加一个辅助 方程。 3-8 用网孔电流法求解题图3-7中电流，。 解：设网孔电流为.2，其绕行方向如题图3-7中所标。列写网孔方程 「2011-10i2-813=-40 -10in+24i2-4ia=-20 -81n-4i2+20i3=20 应用行列式法解上面方程组 20-10-8 120-10-40 4=1024-4=5104,4,=1024-20=-4880 -8-420 -8-420 所以 注：网孔电流法是以假想的网孔电流作为求解量，它仅适用于平面电路。从本题的求解可以归 纳出用网孔电流法求解电路的步骤是： (1)选取网孔电流2，,如网孔电流方向即认为是列网孔WL方程的绕行方向。 (2)列网孔电流方程。观察电路求自电阻R,R2·(一个网孔中所有电阻之和称该网孔的自 电阻，如本题中R,=202,R2=242,R=202,自电阻总为正值)：互电阻R2,R,Rg.(两 网孔公共支路上的电阻之和，如本题中R,=-10,R:=-8,凡=一4，当流过互电阻的两网孔电流 方向一致，互电阻为正值，否则为负值)，等效电压源数值（方程右方为各回路中电压源的代数和， 与网孔电流方向一致的电压源前取负号，否则取正号)。 3.9 用回路电流法求解题图3-7中电流·

（4）求解联立方程组，得到个支路电流， 需要明确：以上支路电流法求解电路的步骤只适用于电路中每一条支路电压都能用支路电 流表示的情况，若电路中含有独立电流源或受控电流源，因其电压不能用支路电流表示，故不能直 接使用上述步骤。此外，若电路中含有受控源，还应将控制量用支路电流表示，即要多加一个辅助 方程。 3-8 用网孔电流法求解题图 3-7 中电流 5 i 。 解：设网孔电流为 1, 2 3 , l l l i i i ，其绕行方向如题图 3-7 中所标。列写网孔方程      − − + = − + − = − − − = − 8 4 20 20 10 24 4 20 20 10 8 40 1 2 3 1 2 3 1 2 3 l l l l l l l l l i i i i i i i i i 应用行列式法解上面方程组 4880 8 4 20 10 24 20 20 10 40 5104, 8 4 20 10 24 4 20 10 8 3 = − − − − − − − =  = − − − − − −  = 所以 i i l 0.956 A 5104 3 4880 5 3 = − − =   = = 注：网孔电流法是以假想的网孔电流作为求解量，它仅适用于平面电路。从本题的求解可以归 纳出用网孔电流法求解电路的步骤是： （1）选取网孔电流 1, 2 3 , l l l i i i ，如网孔电流方向即认为是列网孔 KVL 方程的绕行方向。 （2）列网孔电流方程。观察电路求自电阻 11 22 R R, （一个网孔中所有电阻之和称该网孔的自 电阻，如本题中 11 22 33 R R R =  =  =  20 , 24 , 20 ,自电阻总为正值）；互电阻 12 13 23 R R R , , （两 网孔公共支路上的电阻之和，如本题中 12 13 23 R R R = − = − = − 10, 8, 4 ，当流过互电阻的两网孔电流 方向一致，互电阻为正值，否则为负值），等效电压源数值（方程右方为各回路中电压源的代数和， 与网孔电流方向一致的电压源前取负号，否则取正号）。 3-9 用回路电流法求解题图 3-7 中电流 3 i

解法一：取回路电流为网孔电流，如题图3-7中所示。回路方程同题3-8中方程。 故有 △=5104 △，=-4880 |20-40-8 43=-10-20-4=-12800 -82020 所以 公=会=器0-250784 h=是=解0=-095614 43=i2-i3=-2.5078+0.9561=-1.5517A 解法二：取回路电流如题解39图所示。仅让Ⅱ号回路电流流经1，所在的支路。列 写回路方程。 20 102 82 20. 题解3-9图 [20in-10i2-18i3=-40 -101n+24i2+20i3=-20 -181n+20i2+361=0 用行列式法求上面方程组 20 -10-18 120-40-18 △=-102420=5104，△2=-10-2020=-7920 -182036 -18036 所以 4=6=会-0-15174 显然解法二中回路电流的选取法使计算量减小

解法一：取回路电流为网孔电流，如题图 3-7 中所示。回路方程同题 3-8 中方程。 故有  = 5104 3 = −4880 12800 8 20 20 10 20 4 20 40 8 3 = − − − − − − −  = 所以 i i i A i A i A l l l l 2.5078 0.9561 1.5517 0.9561 5104 4880 2.5078 5104 12800 3 2 3 3 3 2 2 = − = − + = − = − − =   = = − − =   = 解法二：取回路电流如题解 3-9 图所示。仅让Ⅱ号回路电流流经 3 i 所在的支路。列 写回路方程。      − + + = − + + = − − − = − 18 20 36 0 10 24 20 20 20 10 18 40 1 2 3 1 2 3 1 2 3 l l l l l l l l l i i i i i i i i i 用行列式法求上面方程组 7920 18 0 36 10 20 20 20 40 18 5104, 18 20 36 10 24 20 20 10 18 2 = − − − − − − =  = − − − −  = 所以 i i l 1.5517 A 5104 2 7920 3 2 = − − =   = = 显然解法二中回路电流的选取法使计算量减小

注：回路电流法适用于平面或非平面电路，比网孔法更具灵活性。回路法分析电路时，首先要 确定一组基本回路，表定回路电流的绕行方向，其余步骤与网孔法类似。需要指出的是回路电流法 中两回路的共有支路有时会有多条，因而互有电阻的确定要特别细心。否则会发生遗漏互有电阻的 错误。 3-10 用回路电流法求解题图中52电阻中的电流1。 32 厂4 30 50 62 ①16 ①48 题3-10图 解：选取网孔为基本回路，回路电流的绕行方向如图中所示。列回路方程 [12n-6i2=32-48+16=0 -611+17i2-81a=48 -812+1613=0 应用行列式法 12-60 12-60 4=617-8=1920, 43=-61748=4608 0-816 0-80 所以 3-11 用回路电流法求解图示电路中电压U

注：回路电流法适用于平面或非平面电路，比网孔法更具灵活性。回路法分析电路时，首先要 确定一组基本回路，表定回路电流的绕行方向，其余步骤与网孔法类似。需要指出的是回路电流法 中两回路的共有支路有时会有多条，因而互有电阻的确定要特别细心。否则会发生遗漏互有电阻的 错误。 3-10 用回路电流法求解题图中 5 电阻中的电流 i 。 解：选取网孔为基本回路，回路电流的绕行方向如图中所示。列回路方程      − + = − + − = − = − + = 8 16 0 6 17 8 48 12 6 32 48 16 0 2 3 1 2 3 1 2 l l l l l l l i i i i i i i 应用行列式法 4608 0 8 0 6 17 48 12 6 0 1920, 0 8 16 6 17 8 12 6 0 3 = − − − =  = − − − −  = 所以 i i l 2.4 A 1920 3 4608 3 = =   = = 3-11 用回路电流法求解图示电路中电压 Uo

136r①t40 题3-11图 解：回路电流如图中所标。因3A电流源仅与回路I相关，即有，=3A其余两回 路的方程为 -81n+50i2+10ia=136 -181n+10i2+201a=136-50=86 把n=3A带入两个方程中，加以整理得 50i2+10i3=160 10i2+20=140 解得 2=2A 电压 Un=40×i2=40x2=80V 3-12 用回路电流法求解题3-12图所示电路中电流1，及电压U。 9 2.52 14V 1141 152 解：按图示设网孔电流为回路电流。因受控电流源仅和Ⅲ号回路相关，故有 n-1=6-1=5,对回路I和Ⅱ列方程，并代入i3=-0.in有 ∫34i1-4i2+10×0.1i,=0 -4n+10in+5×0.1in=-420 整理得

解：回路电流如图中所标。因 3A 电流源仅与回路Ⅰ相关，即有， i l1 = 3 A 其余两回 路的方程为 18 10 20 136 50 86 8 50 10 136 1 2 3 1 2 3 − + + = − = − + + = l l l l l l i i i i i i 把 i l1 = 3 A 带入两个方程中，加以整理得    + = + = 10 20 140 50 10 160 2 3 2 3 l l l l i i i i 解得 i l 2 = 2 A 电压 Uo = 40i l2 = 40 2 = 80V 3-12 用回路电流法求解题 3-12 图所示电路中电流 a I 及电压 Uo 。 14V + − 15 I a Uo + − 4 1.4I a 2.5 8 2 解 ： 按图示设网孔 电流 为回路 电流 。因受 控电 流源仅 和Ⅲ 号回路 相关 ，故有 n− = − = 1 6 1 5 ，对回路Ⅰ和Ⅱ列方程，并代入 3 1 1 0. l l i = − i 有    − + +  = − − +  = 4 10 5 0.1 420 34 4 10 0.1 0 1 2 1 1 2 1 l l l l l l i i i i i i 整理得

35im-4i2=0 -3.5in+10i2=-420 解得 in=-43.75 公4425-5 i=-0.n=-0.1×(-5)=0.5A 选外层回路列KVL方程20in+1×i2+420-U=0 从中解出 U/=20×(-5)+1×(-43.75)+420=27625V 3-13(需要修改) 用回路电流法求解题图()，(b)两电路中每个元件的功率，并做功率平衡检验。 U. 15 2个2 100(m.3以+ 心中pg号 20 ) 题3-13图 解(a):选取(a)图中网孔为基本回路，回路电流方向如图中所标，列回路方程 in =15 (1) -1xin+3in+2i=10 (2) =4U (3) 式中U。为受控电流源的控制量，需要用回路电流加以表示，所以增补一个方程 U =2x(in +in)=4in (4) 从中解得 in=in 把方程0和(4代入方程(2)中，有-15+32+22=10 即 n==2=5A 各元件的功率分别为

   − + = − − = 3.5 10 420 35 4 0 1 2 1 2 l l l l i i i i 解得 i i A A i i i l l l l l 0.1 0.1 ( 5) 0.5 5 35 4 43.75 35 4 43.75 3 1 2 2 2 = − = −  − = = −  = −  = = − 选外层回路列 KVL 方程 20i l1 +1i l 2 + 420 −U = 0 从中解出 U = 20 (−5) +1 (−43.75) + 420 = 276.25V 3-13 (需要修改) 用回路电流法求解题图(a),(b)两电路中每个元件的功率，并做功率平衡检验。 解(a)：选取(a)图中网孔为基本回路，回路电流方向如图中所标，列回路方程        = −  + + = = U i i i i i l l l l l 4 1 1 3 2 10 15 3 1 2 3 1 (3) (2) (1) 式中 U 为受控电流源的控制量，需要用回路电流加以表示，所以增补一个方程 2 3 4 3 2 ( ) l l l U =  i + i = i  (4) 从中解得 l2 l3 i = i 把方程 (1) 和 (4) 代入方程 (2) 中，有 −15 + 3i l2 + 2i l2 =10 即 i l i l 5 A 5 25 2 = 3 = = 各元件的功率分别为