《电路》课程教学资源（A）习题解答_第5章 含有运算放大器的电阻电路

第5章含有运算放大器的电阻电路 5-1 设要求图示电路的输出为-4。=3,+0.24,已知R,=10k2,求R1和R2 题5-1图 解：题5一1图所示电路中的运放为理想运放，应用其两条规则，有 解法一：由规则1，”=0，得i=i+i2,故 R 根据规则2，得“==0，代入上式中，可得 觉受觉 -=觉+党 代入己知条件，得 鸡+024-是4+是% 故R=号-330，尾=是-0m 解法二：对结点①列出结点电压方程，并注意到规则1，广=0，可得 发局+发加京”=意+觉 应用规则2，得“=0，所以

第 5 章 含有运算放大器的电阻电路 5－1 设要求图示电路的输出 uo 为 1 2 2 − uo = 3u + 0. u ，已知 R3 = 10k ，求 R1 和 R2。 解：题 5－1 图所示电路中的运放为理想运放，应用其两条规则，有 解法一：由规则 1， = 0 − i ，得 1 2 i = i + i ，故 2 2 1 1 3 R u u R u u R uo u − − − − + − = − − 根据规则 2，得 = = 0 − + u u ，代入上式中，可得 （ ） 2 2 1 1 3 2 2 1 1 3 R u R u u R R u R u R u o o − = + − = + 代入已知条件，得 2 1 3 1 1 3 1 2 2 3 0. u R R u R R u + u = + 故， = =  = = k R k R R R 50 0.2 3.33 ; 3 3 2 3 1 解法二：对结点○1 列出结点电压方程，并注意到规则 1， = 0 − i ，可得 2 2 1 1 1 2 3 3 1 ) 1 1 1 ( R u R u u R u R R R + + − o = + − 应用规则 2，得 = 0 − u ，所以

觉觉 =R党+党 后面求解过程和结果同解法一。 注：对含有理想运放电路的分析，需要紧紧抓住理想运放的两条规则：①“虚断”一一倒向端和非 倒向端的输入电流均为零：①“虚短” 一对于公共端（地），倒向端的电压与非倒向输入端的电压 相等。 5-2 题5-2图所示电路起减法作用，求输出电压。和输入电压山、山，之间的关系。 解：根据“虚断”，有：广=十= 得：=i,i=i2 故：6=心=4二北) R R 根据虚短”有：”=rR十风 R. 代入武后得：%=是：-小 解法二：用结点电压法，对结点①和②列出结点电压方程，并注意到规则1，广==0，得 1 1

( ) 2 2 1 1 3 3 2 1 1 3 R u R u u R R u R u R u o o − = + − = + 后面求解过程和结果同解法一。 注：对含有理想运放电路的分析，需要紧紧抓住理想运放的两条规则：○1 “虚断”——倒向端和非 倒向端的输入电流均为零；○2 “虚短”——对于公共端（地），倒向端的电压与非倒向输入端的电压 相等。 5－2 题 5-2 图所示电路起减法作用，求输出电压 o u 和输入电压 1 u 、 2 u 之间的关系。 − + +  R1 R1 R2 R2 + + − + − uo u1 u2 解：根据“虚断”，有： = = 0 − + i i 得： 3 1 4 2 i = i , i = i 故： (1) 1 1 3 0 R u u R u u − − − = − − 而： (2) 2 1 2 2 u R R R u + = + 根据“虚短” 有： 2 1 2 2 u R R R u u + = = − + 代入(1)式后得： ( ) 2 1 1 2 0 u u R R u = − 解法二：用结点电压法，对结点○1 和○2 列出结点电压方程，并注意到规则 1， = = 0 − + i i ，得 (1) 1 ) 1 1 ( 1 1 2 1 1 2 R u u R u R R + n − o =

(2) R2 应用规图2得=，且由武@》知e“R中R,代入方程式中，有 1 ,1、R2 注：简单电路可根据理想运放的两条规则结合KCL和欧姆定律直接分析（见本题解法一），复杂 些的电路用结点电压法分析较方便（见本题解法二）。结点电压法分析含有理想运放电路时需注意： 独立结点取在理想运放的输入端侧，输出端最好不列结点电压方程，因为理想运放的输出端电流是 未知变量。 5-3 求图示电路的输出电压与输入电压之比 解：图示电路较复杂，故采用结点电压法分析。独立结点①和@的选取如图所示，列出结点电压方 程，并注意到规则1，广=0，可得 (G,+G3+G+G)un1-G42-G42=G4 -G,41+(G3+G,)4n2-G,4,=0 应用规则2，得“：=0，所以，以上两式变为 (G,+G2+G4+G)m1-G,4=G4 4=G G 题5-3酒 把第二式代入第一式中，可得 告=a+0+0aa,+God GG. 注：本题求解的关键是正确列出结点电压方程。注意列方程时，勿将各结点与输出电压U2之间的 互导项遗漏。 5-4 求图示电路得电压比值丛

) (2) 1 1 ( 1 2 2 1 2 R u u R R + n = 应用规则 2，得 un1 = un2 ，且由式（2）知， 2 1 2 2 2 u R R R un + = ，代入方程式（1）中，有 ) ( ) 1 1 ( 2 1 1 2 2 1 2 2 1 2 1 2 1 2 u u R R u R R R R R u R R R uo = − + = − + + 注：简单电路可根据理想运放的两条规则结合 KCL 和欧姆定律直接分析（见本题解法一），复杂一 些的电路用结点电压法分析较方便（见本题解法二）。结点电压法分析含有理想运放电路时需注意： 独立结点取在理想运放的输入端侧，输出端最好不列结点电压方程，因为理想运放的输出端电流是 未知变量。 5－3 求图示电路的输出电压与输入电压之比 1 2 u u 。 解：图示电路较复杂，故采用结点电压法分析。独立结点○1 和○2 的选取如图所示，列出结点电压方 程，并注意到规则 1， = 0 − i ，可得 ( ) 0 ( ) 4 1 3 4 2 3 2 1 2 4 5 1 4 2 5 2 1 1 − + + − = + + + − − = G u G G u G u G G G G u G u G u G u n n n n 应用规则 2，得 un2 = 0 ，所以，以上两式变为 2 4 3 1 1 2 4 5 1 5 2 1 1 ( ) u G G u G G G G u G u G u n n = − + + + − = 把第二式代入第一式中，可得 1 2 4 5 3 4 5 1 4 1 2 (G G G G )G G G G G u u + + + + = − 注：本题求解的关键是正确列出结点电压方程。注意列方程时，勿将各结点与输出电压 U2 之间的 互导项遗漏。 5－4 求图示电路得电压比值 u1 uo

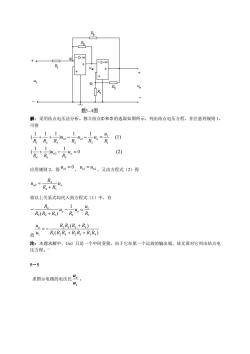
FD 题5-4图 解：采用结点电压法分析。独立结点①和②的选取如图所示，列出结点电压方程，并注意到规则1， 可得 =0 (2) 应用规则2，得“1=0,1=”2，又由方程式(2)得 a=R+R” 将以上关系式均代入到方程式(1)中，有 厂尼设+R”元=觉 皮名品风 RR(R+Rs) 注：本题求解中，U01只是一个中间变量，由于它在第一个运放的输出端，故无需对它列出结点电 压方程。 5-5 求图示电路的电压比

解：采用结点电压法分析。独立结点○1 和○2 的选取如图所示，列出结点电压方程，并注意到规则 1， 可得 0 (2) 1 ) 1 1 ( (1) 1 1 ) 1 1 1 ( 5 2 4 5 1 1 3 1 2 1 1 2 3 + − = + + − − = n o n o o u R u R R R u u R u R u R R R 应用规则 2，得 un1 = 0， uo1 = un2 ，又由方程式（2）得 n uo R R R u 4 5 4 2 + = 将以上关系式均代入到方程式（1）中，有 1 ( ) 1 1 2 4 5 3 4 R u u R u R R R R o − o = + − 故 ( ) ( ) 1 2 4 2 5 3 4 2 3 4 5 1 R R R R R R R R R R R u uo + + + = − 注：本题求解中，Uo1 只是一个中间变量，由于它在第一个运放的输出端，故无需对它列出结点电 压方程。`` 5－5 求图示电路的电压比 s o u u

题5-图 解法一：采用结点电压法分析。独立结点①和②的选取如图所示，列出结点电压方程，并注意到规 则1，可得 应用规则2，得：=0，代入上述方程中得， =是 ,故有 整理后得 总-见风+是+风 题解-5图 解法二：将题5一5图中得结点⑦左边的有源一端口电路等效为理想电压源和电阻的串联电路，如题 解5一5图所示，其中 R、 此电路为一个倒向比例器，故有

解法一：采用结点电压法分析。独立结点○1 和○2 的选取如图所示，列出结点电压方程，并注意到规 则 1，可得 0 1 ) 1 1 ( 1 ) 1 1 1 ( 4 2 3 3 4 1 1 2 3 1 1 2 3 − + + − = + + − = n o n s n n u R u R R R u R u u R u R R R 应用规则 2，得 un2 = 0 ，代入上述方程中得， n uo R R u 4 3 1 = − ，故有 4 1 3 1 2 3 )( ) 1 1 1 ( R u u R R R R R s + + − o = 整理后得 1 2 2 3 3 1 2 4 R R R R R R R R u u s o + + = − 解法二：将题 5－5 图中得结点○2 左边的有源一端口电路等效为理想电压源和电阻的串联电路，如题 解 5－5 图所示，其中 1 2 3 1 2 2 u , R (R // R ) R R R R uoc s eq = + + = 此电路为一个倒向比例器，故有

《=是=限虎R见 R2 业一R风+R+RR RR 5-6 试证明题5-6图所示电路若满足RR,=R2R,则电流i,仅决定于，而与负载电阻R无关。 题5-6图 解：采用结点电压法分析。独立结点①和②的选取如图所示，列出结点电压方程，并注 意到规则1，可得 只定克觉 发+尼+月尼u=0 应用规则2，有1=a,代入以上方程中，整理得 《=风贫n 分是贵 放：“因R-微-RRR4又因为=资风R-R损-RRR4 当RR=RR,时，即电流1，与负载电阻R,无关，而知与电压4有关。 7 求题5-7图所示电路的山。和输入电压4s1、山s2之间的关系

1 2 2 3 1 3 2 4 1 2 2 1 2 3 4 4 ( // ) R R R R R R R R u u u R R R R R R R u R R u s o oc s eq o + + = − +  + = − = − 5-6 试证明题 5-6 图所示电路若满足 R1R4 = R2R3 ，则电流 L i 仅决定于 1 u 而与负载电阻 RL 无关。 − + +  R1 R4 R3 R2 + − u1 iL RL 题 5-6 图 解：采用结点电压法分析。独立结点○1 和○2 的选取如图所示，列出结点电压方程，并注 意到规则 1，可得 0 1 ) 1 1 1 ( 1 ) 1 1 ( 4 2 1 2 1 1 2 1 1 2 + + − = + − = n o L n o u R u R R R R u u R u R R 应用规则 2，有 un1 = un2 ，代入以上方程中，整理得 2 3 4 4 ) 1 1 1 ( n L o u R R R u = R + + 1 1 2 2 4 2 3 4 1 ) 1 ( R u u R R R R R R R n L − − = 故 1 2 3 1 4 1 3 4 2 3 2 ( ) u R R R R R R R R R R R u L L n − − = 又因为 1 2 3 1 4 1 3 4 2 2 3 ( ) u R R R R R R R R R R R u i L L n L − − = = 当 R1R4 = R2R3 时，即电流 L i 与负载电阻 RL 无关，而知与电压 1 u 有关。 5-7 求题 5-7 图所示电路的 o u 和输入电压 S1 u 、uS2 之间的关系

题57图 解：采用结点电压法分析。独立结点①和②的选取如图所示，列出结点电压方程，并注 意到规则1，得（为分析方便，用电导表示电阻元件参数） (G+G)wn1-G,4。=G41 (G3+G)4e-G4。=-G34, 应用规则2，有=42，代入上式，解得4，为 4.=G(G,+G+GG+G,m或为u.-R(B,+R,+RR+Rm GG-G,G3 R2R3-RR 5-8 电路如图所示，设R,=16R，验证该电路的输出4。与输入1~4之间的关系为 4。=(841+42+2山3+山，)。[注：该电路为4位数模转换器，常用在信息处理、自动控制领域。 该电路可将一4位二进制数字信号转换成模拟信号，例如当数字信号为101时，令 4=42=,=1,43=0，则由关系式。=-(8仙，+42+23+，)得模拟信号 4。=-(8+4+0+1)=-13。】 2R12n1 %4 题5-9图

− + +  R1 R4 R2 + + − − − uS2 uS1 R3 + uo 题 5-7 图 解：采用结点电压法分析。独立结点○1 和○2 的选取如图所示，列出结点电压方程，并注 意到规则 1，得（为分析方便，用电导表示电阻元件参数） 3 4 2 4 3 2 1 2 1 2 1 1 ( ) ( ) n o s n o s G G u G u G u G G u G u G u + − = − + − = 应用规则 2 ，有 un1 = un2 ，代入上式，解得 o u 为 1 4 2 3 1 3 4 1 3 1 2 2 ( ) ( ) G G G G G G G u G G G u u s s o − + + + = 或为 2 3 1 4 2 3 4 1 4 1 2 2 ( ) ( ) R R R R R R R u R R R u u s s o − + + + = 5－8 电 路 如 图 所 示 ， 设 Rf = 16R ， 验 证 该 电 路 的 输 出 uo 与输入 u1 ~ u4 之 间 的 关 系 为 (8 4 2 ) uo = − u1 + u2 + u3 + u4 。[注：该电路为 4 位数模转换器，常用在信息处理、自动控制领域。 该电路可 将一 4 位二 进制数 字信号 转换 成模拟 信号， 例如 当数字 信号为 1101 时，令 u1 = u2 = u4 = 1 ， u3 = 0 ，则由关系式 (8 4 2 ) uo = − u1 + u2 + u3 + u4 得模拟信号 uo = −(8 + 4 + 0 + 1) = −13 。]

解：应用电源等效变换把题5一9图示电路等效为题解5一9所示，得其等效参数：R,=R 题解-9图

解：应用电源等效变换把题 5－9 图示电路等效为题解 5－9 所示，得其等效参数： Req = R