《电路》课程教学资源（A）习题解答_第10章 含有耦合电感的电路

第10章含有耦合电感的电路 10-1 试确定图示耦合线圈的同名端。 1 1 91 琪 2223 1 题10-1图 解：耦合线圈的同名端是这样规定的：当电流分别从两线圈各自的某端同时流人（或流出）时，若两 者产生的磁通相助，则这两端称为耦合线圈的同名端 根据同名端的定义，图（®）中，假设电流，分别从端子1和端子2中流入，按右手螺旋法则可得， 产生的磁通链（用实线表示）方向与1，产生的磁通链（用虚线表示）方向相反如图(a)所示，显然它们 互相“削弱”，所以判定端子1与端子2为异名端，那么，同名端即为(1,2')或(1'，2)。 对图(b),分析过程同图(a)。判断同名端为：(1,2')，(1,3)，(2,3')。 10-2 两个具有耦合的线圈如图所示。 (1)标出它们的同名端：(2)当图中开关S闭合时或闭合后再打开时，试根据毫伏表的 偏转方向确定同名端。 1 2 题10-2图 解：(1)根据同名端定义和两个线圈的绕向采用题10一1中的分析方法，判定同名端为(1,2)， 如题10一2图中所示。 (2)图示电路是测试耦合线圈同名端的实验线路。当开关S迅速闭合时，线圈1中有随时间增 大的电流从电源正极流入线图端子1，这时>0，则毫伏表的高电位端与端子1为同名端。当开关 S闭合后再打开时，电流1，减小，毫伏表的低电位端与端子1为同名端。 注：从耦合线圈同名端的规定（见10一1题解）可以得出如下含意(1)耦合线圈的同名 端只与两线圈的绕向及两线圈的相互位置有关，与线圈中电流参考方向如何假设无关：(2) 当两电流均从同名端流入（或流出），两线圈中的磁通是相助的，两线圈上的自感压降和互感 压降方 向一致 止 名 端的含意，对正确判定耦合线圈的同名端和正确书写耦合线圈 上的电压、电流关系式是至关重要的。 10-3 若有电流i=2+5cos(10t+30)4,2=10eA,各从题10-1图(a)所示线圈的1端和

第 10 章 含有耦合电感的电路 10－1 试确定图示耦合线圈的同名端。 题 10－1 图 解: 耦合线圈的同名端是这样规定的：当电流分别从两线圈各自的某端同时流人（或流出）时，若两 者产生的磁通相助，则这两端称为耦合线圈的同名端。 根据同名端的定义，图（a）中，假设电流 i1，i2 分别从端子 1 和端子 2 中流入，按右手螺旋法则可得， i1 产生的磁通链（用实线表示）方向与 2 i 产生的磁通链（用虚线表示）方向相反如图（a）所示，显然它们 互相“削弱”，所以判定端子 1 与端子 2 为异名端，那么，同名端即为(1，2’)或(1’，2)。 对图（b），分析过程同图（a）。判断同名端为：(1，2’)，(1，3’)，(2，3’)。 10－2 两个具有耦合的线圈如图所示。 （1）标出它们的同名端；（2）当图中开关 S 闭合时或闭合后再打开时，试根据毫伏表的 偏转方向确定同名端。 题 10-2 图 解：（1）根据同名端定义和两个线圈的绕向采用题 10－1 中的分析方法，判定同名端为（1，2）， 如题 10－2 图中所示。 （2）图示电路是测试耦合线圈同名端的实验线路。当开关 S 迅速闭合时，线圈 1 中有随时间增 大的电流 1 i 从电源正极流入线圈端子 1，这时 0 (1) 1  dt di ，则毫伏表的高电位端与端子 1 为同名端。当开关 S 闭合后再打开时，电流 1 i 减小，毫伏表的低电位端与端子 1 为同名端。 注：从耦合线圈同名端的规定（见 10－1 题解）可以得出如下含意（1）耦合线圈的同名 端只与两线圈的绕向及两线圈的相互位置有关，与线圈中电流参考方向如何假设无关；（2） 当两电流均从同名端流入（或流出），两线圈中的磁通是相助的，两线圈上的自感压降和互感 压降方向一致。正确理解同名端的含意，对正确判定耦合线圈的同名端和正确书写耦合线圈 上的电压、电流关系式是至关重要的。 10－3 若有电流 i 1 2 5cos(10t 30 )A  = + + ，i e A 5t 2 10 − = ，各从题 10－1 图（a）所示线圈的 1 端和

2端流入，并设线圈1的电感L=6H,线圈2的电感L2=3H,互感为M=4H。试求：(1) 各线圈的磁通链；(2)端电压4，和4z:(3)耦合因素k。 解：如上面题10一1图(a)所示的耦合线圈，设电流i和2，分别从各自线圈的1端和2 端流入按右手螺旋法则有，1产生的磁通链（用实线表示）方向和，产生的磁通链（用虚线表 示)方向如图(a)所示 1)耦合线圈中的磁通链是自感磁通链和互感磁通链的代数和，所以，根据题10 一1图(a)所示的磁通链方向，有 4=41-2=L4-h, =[12+30cos(101+30)-40e-]W% 4=-1+w2=-M+L4 =-8-20C0S101+30°)+30e-]Wwb (2)由上述可得端电压 -警-40-告-010+0)+20e*y dt -=-w高+4产-2o0m10+30)-150e*y (3)根据耦合因素k的定义，有 “品方094好 注：本题求解说明，当两电流从异名端流入时，两线圈中的磁通相消，自感压降与互感 压降异号。 10-4 图示电路中L=6H,L2=3H,M=4H。试求从端子1-1'看进去的等效电感。 解：题10一5图示的去耦等效电路或原边等效电路如题解10一5图所示。 (1)由题解10-5图()所示的去耦等效电路（原电路同名端异侧联接），可求得从端 子1-1'看进去的等效电感为 Lg=(L+M0+(L2+M0M(-M)=10+7(-4)=0.667H (2)由题解10一5图(b)所示的等效去耦等效电路（原电路同名端同侧联接），可求得 从端子1-'看进去的等效电感为 L=(L-M0+(L2-M0IM=2+-1I4=0.667H

2 端流入，并设线圈 1 的电感 L1 = 6H ，线圈 2 的电感 L2 = 3H ，互感为 M = 4H 。试求：（1） 各线圈的磁通链；（2）端电压 u11 和 u22 ；（3）耦合因素 k。 解：如上面题 10－1 图（a）所示的耦合线圈，设电流 1 i 和 2 i 分别从各自线圈的 1 端和 2 端流入按右手螺旋法则有， 1 i 产生的磁通链（用实线表示）方向和 2 i 产生的磁通链（用虚线表 示）方向如图（a）所示。 （1）耦合线圈中的磁通链是自感磁通链和互感磁通链的代数和，所以，根据题 10 －1 图（a）所示的磁通链方向，有 1 11 12 1 1 Mi2  = − = Li − t e Wb t [12 30cos(10 30 ) 40 ] −5 = + + −  COS t e Wb Mi L i t [ 8 20 (10 30 ) 30 ] 5 2 21 22 1 2 2 − = − − + + = − + = − +     （2）由上述可得端电压 t e V dt dt L dt di M dt d u t e V dt di M dt dt L dt d u t t [200sin(10 30 ) 150 ] [ 300sin(10 30 ) 200 ] 2 5 2 2 1 22 1 2 5 1 1 11 −  −  = = − + = + − = = − = − + +     （3）根据耦合因素 k 的定义，有 0.943 3 2 4 1 2 = = = L L M k 注：本题求解说明，当两电流从异名端流入时，两线圈中的磁通相消，自感压降与互感 压降异号。 10－4 图示电路中 L1 = 6H ， L2 = 3H ， M = 4H 。试求从端子 1−1 看进去的等效电感。 解：题 10－5 图示的去耦等效电路或原边等效电路如题解 10－5 图所示。 （1）由题解 10－5 图（a）所示的去耦等效电路（原电路同名端异侧联接），可求得从端 子 1−1 看进去的等效电感为 Leq = (L1 + M ) + (L2 + M )//(−M ) =10 + 7//(−4) = 0.667H （2）由题解 10－5 图（b）所示的等效去耦等效电路（原电路同名端同侧联接），可求得 从端子 1−1 看进去的等效电感为 Leq = (L1 − M ) + (L2 − M )//M = 2 + (−1)//4 = 0.667H

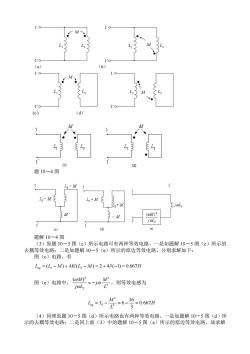
10 10 M L L2 1"0 I'o (a) (h) 1o- (ch 题10-4图 马-M L-M 题解10-4图 (3)原题10-5图(c)所示电路可有两种等效电路，一是如题解10-5图(c)所示的 去耦等效电路： 二是如题解10一5(e)所示的原边等效电路。分别求解如下： 图(c)电路，有 L=(L-M0+M(L2-M)-2+4-)=0.667H 图心电路中，a2。-加艺，则等效电感为 M b=h-答=6-9=067H (4)同理原题10-5图(d)所示电路也有两种等效电路，一是如题解10-5图(d)所 示的去耦等效电路：二是同上面(3)中的题解10一5图（©）所示的原边等效电路，故求解

L1 1 M L2 1' L1 1 M L2 1' （a） （b） L1 1 M L2 1' L1 1 M L2 1' (c ) （d） 题 10－4 图 题解 10－4 图 （3）原题 10－5 图（c）所示电路可有两种等效电路，一是如题解 10－5 图（c）所示的 去耦等效电路；二是如题解 10－5（e）所示的原边等效电路。分别求解如下： 图（c）电路，有 Leq = (L1 − M ) + M//(L2 − M ) = 2 + 4//(−1) = 0.667H 图（e）电路中， 2 2 2 2 ( ) L M j j L M    = − ，则等效电感为 H L M Leq L 0.667 3 16 6 2 2 = 1 − = − = （4）同理原题 10－5 图（d）所示电路也有两种等效电路，一是如题解 10－5 图（d）所 示的去耦等效电路；二是同上面（3）中的题解 10－5 图（e）所示的原边等效电路，故求解

结果相同。对图(d)去耦等效电路，求得从端子1-1'看进去得等效电感为 L=(L+M)+(-M)M(L2+M0=10+(-4)/7=0.667H 注：耦合电感的去耦等效是分析含耦合电感电路的一种常用方法，它主要有：(1)耦合 电感串联去耦两端等效和T型去耦多端等效：(2)用受控源表示耦合关系：(3)原边（或副 边)等效电路法（一般用于空心变压器电路）。应用去耦等效方法时应当明确： (1)去耦等效是对耦合电感端子以外的电压、电流、功率的等效： (2)其等效电感参数不但与两耦合线圈的自感系数L,L,和互感系数M有关，而且与 同名端的位置有关。如耦合电感串联去耦等效分顺接（两串接线圈异名端相联），有 L,=L+L2+2M和反接（两串接线圈同名端相联），有L,=L+L2-2M两种情况，耦合电 感的T型去耦等效分同名端同侧联接（如题10-5(b),(c)图）和异侧联接（如题10一5(a), (d)图)两种情况 10-5 求图示电路的输入阻抗Z(o=lrad/s). t 6 题10-6图 解：题10一6图示电路的原边等效电路和去耦等效电路如题解10一6图所示。 1 0.2 题解10 -6图 (1)题解10-6图(a)所示的原边等效电路中，Z2=1+j22,故输入阻抗为 z=L+a2-jt中202+060 (2)由题解10一6图(b)所示的去耦等效电路，可得 Z=-1+U2U5-j02=-10 (3)题解10-6图（©）所示的串联去耦等效电路中，等效电感为：Lm=2+3-4=1H

结果相同。对图（d）去耦等效电路，求得从端子 1−1 看进去得等效电感为 Leq = (L1 + M ) + (−M )//(L2 + M ) =10 + (−4)//7 = 0.667H 注：耦合电感的去耦等效是分析含耦合电感电路的一种常用方法，它主要有：（1）耦合 电感串联去耦两端等效和 T 型去耦多端等效；（2）用受控源表示耦合关系；（3）原边（或副 边）等效电路法（一般用于空心变压器电路）。应用去耦等效方法时应当明确： （1）去耦等效是对耦合电感端子以外的电压、电流、功率的等效； （2）其等效电感参数不但与两耦合线圈的自感系数 L1， L2 和互感系数 M 有关，而且与 同名端的位置有关。如耦合电感串联去耦等效分顺接（两串接线圈异名端相联），有 Leq = L1 + L2 + 2M 和反接（两串接线圈同名端相联），有 Leq = L1 + L2 − 2M 两种情况，耦合电 感的 T 型去耦等效分同名端同侧联接（如题 10－5（b），(c)图）和异侧联接（如题 10－5（a）， （d）图）两种情况。 10－5 求图示电路的输入阻抗 Z( =1rad s)。 题 10－6 图 解：题 10－6 图示电路的原边等效电路和去耦等效电路如题解 10－6 图所示。 题解 10 －6 图 （1）题解 10－6 图（a）所示的原边等效电路中， Z22 =1+ j2 ，故输入阻抗为 = +  + = + = + (0.2 0.6) 1 2 ( ) 1 22 2 1 j j j Z M Z j L   （2）由题解 10－6 图（b）所示的去耦等效电路，可得 = − + − ) = − 1 0.2 1 Z j1 ( j2)//( j5 j j (3)题解 10－6 图（c）所示的串联去耦等效电路中，等效电感为： Leq = 2 + 3 − 4 = 1H

且0= ,C1,故此电路处于并联诺振状态，则输入阻抗为Z:0. 10-6 图示电路中R=R=12,aL1=32,L2=22,M=22,U=100P。求： (1)开关S打开和闭合时的电流：(2)S闭合时各部分的复功率。 Ui. 148 a 题10-6图 解：本题可用去耦等效电路计算。等效电路如题解10一7图所示， 14名j@%+如 + ja(L+M) +M) R 题解10-7图 设0，=100∠0V,则 (1)开关S打开时 1风+现+品5+而一g 100 =2+79922847 =10.85∠-77.47°A 开关S闭合时 100∠0° =R+aL+M+R+7mL+M-oM万-1+5+1+j9-西 =43.85∠-37.88A (2)开关S闭合时电源发出的复功率为 5=0,i1=100×43.85∠37.88°=4385∠37.88°VA 因此时，线圈2被短路，其上的电压0，=0，则线圈1上的电压心，=U,故 线圈2吸收的复功率为：S,=0

且 rad s LeqC 1 1  = = ，故此电路处于并联谐振状态，则输入阻抗为 Z =  。 10－6 图示电路中 R1 = R2 =1，L1 = 3，L2 = 2，M = 2，U1 =100V 。求： （1）开关 S 打开和闭合时的电流 İ1；（2）S 闭合时各部分的复功率。 题 10-6 图 解：本题可用去耦等效电路计算。等效电路如题解 10－7 图所示， 题解 10-7 图 设 U V   1 =1000 ，则 （1）开关 S 打开时 ω( ) 1 2 1 2 1 1 R R j L L M U I + + + + =     9.22 88.47 100 2 9 100 0  = +  = j A  = 10.85 − 77.47 开关 S 闭合时 ω( ) [ ω( )]//( ω ) 1 1 2 2 1 1 R j L M R j L M j M U I + + + + + − =   1 5 (1 4)//( 2) 100 0 + j + + j − j  =  43.85 37.88 A =  − （2）开关 S 闭合时电源发出的复功率为 S U1 I 1 100 43.85 37.88 4385 37.88 VA   =   =   =   因此时，线圈 2 被短路，其上的电压 0 2 U  L = ，则线圈 1 上的电压 UL1 U1  =  ，故 线圈 2 吸收的复功率为： 0 2 SL =

线圈1吸收的复功率为：5，=5=4385∠37.88°VA 10-7 把两个线圈串联起来接到50Hz,220V的正弦电源上，顺接时得电流1=2.7A,吸收的功 率为218.7W:反接时电流为7A。求互感M。 解：按题意知：U,=220P,o=2可=314ad/s,则当两个线圈顺接时，等效电感为： L+L2+2M等效电阻为 R-片-27-30m 则总阻抗为 R+o4++2w0-9- M++2w0=-0=75758 (1) 而当两个线圈反接时，等效电感为：L1+L2一2M。 则总阻抗为 R+o4+6-2w-号=9 故 au+6-2w0-29-30=9368 (2) 用式(1)减去(2)可求得： M=75.758-9368-5286mH 40 本题给出了一种测量计算两线圈互感系数的方法。 10-8 电路如题10-8图所示，已知两个线圈的参数为：R=R=100,L1=3H,L=10H,M=5H,正弦电 源的电压U=220V,w=100rds。 ()试求两个线圈端电压，并做出电路的相量图： (2)证明两个耦合电感反接串联时不可能有L1+L2-2M0 (3)电路中串联多大的电容可使电路发生串联谐振： (④画出该电路的去耦等效电路。 + +立- joM 0 立2+0 0+0 一 题10-8图 解：图示电路中的两个耦合线圈为反接串联，所以其等效电感为： Lm=L+L2-2M=3H

线圈 1 吸收的复功率为： SL S 4385 37.88 VA 1  = =  10－7 把两个线圈串联起来接到 50Hz，220V 的正弦电源上，顺接时得电流 I = 2.7A ，吸收的功 率为 218.7W；反接时电流为 7A。求互感 M。 解：按题意知： Us = 220V ， = 2f = 314rad s ，则当两个线圈顺接时，等效电感为： L1 + L2 + 2M 等效电阻为 = = = 30 2.7 218.7 2 2 I P R 则总阻抗为 2.7 220 ( 2 ) 2 1 2 2 2 + + + = = I U R L L M S  故 ) 30 75.758 2.7 220 ( 2 ) ( 2 2  L1 + L2 + M = − = （1） 而当两个线圈反接时，等效电感为： L1 + L2 − 2M 。 则总阻抗为 7 220 ( 2 ) 2 1 2 2 2 + + − = = I U R L L M s  故 ) 30 9.368 7 220 ( 2 ) ( 2 2  L1 + L2 − M = − = （2） 用式（1）减去（2）可求得： M 52.86mH 4 75.758 9.368 = − =  本题给出了一种测量计算两线圈互感系数的方法。 10－8 电路如题 10-8 图所示，已知两个线圈的参数为： R1= R2 =100Ω ，L1=3H，L2=10H，M=5H，正弦电 源的电压 U=220V，ω=100rad/s。 (1) 试求两个线圈端电压，并做出电路的相量图； (2) 证明两个耦合电感反接串联时不可能有 L1+L2-2M≤0 (3) 电路中串联多大的电容可使电路发生串联谐振； (4) 画出该电路的去耦等效电路。 1 U2 U ＋ － ＋ － R1 R2 ＋ － • • U 1 jL 2 jL jM I 1 U2 U ＋ － ＋ － R1 R2 ＋ － • • U 1 jL 2 jL jM 1 U2 U ＋ － ＋ － R1 R2 ＋ － • • U 1 jL 2 jL jM I 题 10-8 图 解：图示电路中的两个耦合线圈为反接串联，所以其等效电感为： Leq = L1 + L2 − 2M = 3H

令0=220∠0V,故电流i为 +R+joL20+7300=0.61∠-56.3r 7 I= 220∠0° (1)两个线圈端电压心，和立，的参考方向如图所示，则 U,=[R+jo(L-M)]i=(100-j200)×0.61∠-56.31 =1364∠-11974°V U2=[R+jm(L2-M0i-100+j500)×0.61∠-56.31° -311.04∠22.38°V 电路相量图如题解10一8图(a)所示。 -jaM jaL! 0 +1R R2 (b) 题解10-8图 (2)只要证明两个耦合电感反接串联时，有L+L2-2M≥0即可。证明如下 因为(D-L2)2≥0，故L+L2-2LL≥0 即L+L222√4 又根据耦合因数k= M =≤1，即M≤V LL 所以 L+L2≥2M,或L+L2-2M≥0 1 （G)因为串联诺报的条件是：以，d=0,即0=C 所以C=o7,1wx333

令 U V   = 2200 ，故电流 I  为     0.61 56.31 200 300 220 0 1 2 =  − +  = + + = R R j L j U I  eq （1）两个线圈端电压 U1  和 U2  的参考方向如图所示，则    U1 = [R1 + j(L1 − M)]I = (100 − j200)0.61− 56.31 V  =136.4 −119.74    U2 = [R2 + j(L2 − M)]I = (100 + j500)0.61− 56.31 V  = 311.0422.38 电路相量图如题解 10－8 图（a）所示。 题解 10－8 图 （2）只要证明两个耦合电感反接串联时，有 L1 + L2 − 2M  0 即可。证明如下 因为 ( ) 0 2 L1 − L2  ，故 L1 + L2 − 2 L1L2  0 即 L1 + L2  2 L1L2 又根据耦合因数 1 1 2 =  L L M k ，即 M  L1L2 所以 L1 + L2  2M ，或 L1 + L2 − 2M  0 （3）因为串联谐振的条件是： 0 1 − = C Leq   ,即 LeqC 2 1  = 所以 F L C eq   33.33 100 3 1 1 2 2 =  = =

(4)该电路两个耦合线圈是反接串联，所以去耦等效电路如图(b)所示。 10-9 题10-9图所示电路，L1=02H,L2=M0.1H,us14.14c0s2+30V。求图中表W的读数，并说明该读 数有无实际意义。 0s=10∠30 10-12 图示电路中图示电路中R=ln,以=2no叫=2n,aM=80,之32n.求电 流i,和电压02 题10-12图 解法一：用题解10-13图(a)所示的原边等效电路求电流i,其中， 乙：=/®以+6G2-2=0,即副边电路处于谐振状态。故反映阻抗为 （oM0- Z22 所以，电流i=0。 (aM02 (a02 (

（4）该电路两个耦合线圈是反接串联，所以去耦等效电路如图（b）所示。 10－9 题 10-9 图所示电路，L1=0.2H，L2=M=0.1H，us=14.14cos(2t+30º)V。求图中表 W 的读数，并说明该读 数有无实际意义。 ύS=10∠30 10－12 图示电路中图示电路中 R1 =1， 2 , L1 =  L2 = 32，M = 8Ω， = 32 1 C 。求电 流 1 I  和电压 U2  。 题 10－12 图 解法一： 用题解 10－13 图（a）所示的原边等效电路求电流 1 I  ，其中， 32 32 0 1 2 22 = 2 + = j − j = j C Z j L   ，即副边电路处于谐振状态。故反映阻抗为 =  22 2 ( ) Z M 所以，电流 I 1 = 0 

题解10-13图 用图(b)所示的副边等效电路求电压心，其中，乙，=R+j®L,=(1+2)2,则反映阻 抗为 (M =64=2862∠-63.490 等效电源电压为 必=品w-2s7V Zu 故，电压ù，为 -j32 0/2+286222634g-728622657=3240V 电压心，的另一解法：如题10一13图所示，因为=0，所以，初级回路中的互感电压为 a-,则贴点gnA 故 U:=-joC: 12=32x(-川=32∠0V 解法二： _原电路的T型去耦等效电路如题解10一13图（©）所示。应用网孔分析法 设网孔电流如图(c)中所标示。网孔方程为 1+j2)i+j813=8∠0° 81+j24+8-32)12=0 由第2式得i,=0,代入第1式中，解得i2=-jA,故电压 02=-(-32)×i2=32∠0°V 10-13 己知空心变压器如图()所示，原边的周期性电流源波形如图(b)所示（一个周期）， 副边的电压表读数（有效值）为25V。 画出副边端电压的波形，并计算互感M: 给出它的等效受控源(CCVS)电路： 如果同名端弄错，对(1)，(2)的结果有无影响？

题解 10－13 图 用图（b）所示的副边等效电路求电压 U2  ，其中， Z11 = R1 + jL1 = (1+ j2) ，则反映阻 抗为 =  −  + = 28.62 63.43 1 2 ( ) 64 11 2  Z j M 等效电源电压为 8 0 28.62 26.57 V 1 2 8 1 11      =  + = j j U Z jM 故，电压 U2  为 28.62 26.57 32 0 V 32 28.62 63.43 32 32 2       =  +  − − − = j j j U 电压 U2  的另一解法：如题 10－13 图所示，因为 I 1 = 0  ，所以，初级回路中的互感电压为 2 U1 j MI   =  ，则 1 A 8 1 8 0 2 j j M j U I = −  = =     故 32 ( 1) 32 0 V 1 2 2 2   = − I  = j  − j =  j C U  解法二： 原电路的 T 型去耦等效电路如题解 10－13 图（c）所示。应用网孔分析法， 设网孔电流如图（c）中所标示。网孔方程为    + + − = + + =  8 (24 8 32) 0 (1 2) 8 8 0 1 2 1 2 j I j I j I j I      由第 2 式得 I 1 = 0  ，代入第 1 式中，解得 I  2 = − jA ，故电压 2 ( 32 ) 2 32 0 V  U  = − − j  I  =  10－13 已知空心变压器如图（a）所示，原边的周期性电流源波形如图（b）所示（一个周期）， 副边的电压表读数（有效值）为 25V。 画出副边端电压的波形，并计算互感 M； 给出它的等效受控源（CCVS）电路； 如果同名端弄错，对（1），（2）的结果有无影响？

十/A (a 6 题10-14图 解：(1)由于图(a)中的空心变压器副边接理想电压表，视为开路，则其电流为零。副 边端电压山为互感电压，由其参考方向，可得 女=-M (1) 由图(b)可写出i,(0的分段函数表达式为 月1A0s1s4s 1,0= (2) 221+10A4s1s5s 将式(2)代入到式(1)中，经微分运算得电压山，为 Mr0≤1≤45 U2={2 (3) 2MV4≤t≤5s 根据有效值定义，知端电压，的有效值为 4-Gh-h+2wr询=Mv 又己知，U2=25V,则M=25H 由式(3)和互感M值，可画出副边端电压山，的波形如题解10一14图(a)所示。 (2)题10-14图(a)的等效控源(CCVS)电路如题解10-14图(b)所示。 (3)如果同名端弄错，对互感M值和电压表读数无影响：(1)中的4，()和(2)结果中 的受控源(CCVS)的方向将相反

题 10－14 图 解：（1）由于图（a）中的空心变压器副边接理想电压表，视为开路，则其电流为零。副 边端电压 2 u 为互感电压，由其参考方向，可得 dt di u M s 2 = − （1） 由图（b）可写出 i (t) s 的分段函数表达式为     − +     = t A t s t A 0 t s i t s 2 10 4 5 4 2 1 ( ) （2） 将式（2）代入到式（1）中，经微分运算得电压 2 u 为       −   = t s V 0 t s U 2M V 4 5 4 2 M 2 （3） 根据有效值定义，知端电压 2 u 的有效值为 ) (2 ) ] V 2 [ ( 5 1 1 5 4 2 4 0 2 0 2 2 2 dt M dt M M u dt T u T = = − + =    又已知， U2 = 25V ，则 M = 25H 由式（3）和互感 M 值，可画出副边端电压 2 u 的波形如题解 10－14 图（a）所示。 （2）题 10－14 图（a）的等效控源（CCVS）电路如题解 10－14 图（b）所示。 （3）如果同名端弄错，对互感 M 值和电压表读数无影响；（1）中的 ( ) 2 u t 和（2）结果中 的受控源(CCVS)的方向将相反