《电路》课程教学资源（A）习题解答_第14章 线性动态电路的复频域分析

第14章线性动态电路的复频域分析 141求下列各函数的像函数： ()ft)=1-e (2)f(t)=sin(at+) (3)f=e(1-am) ④f0=上a-e) (⑤f)=t2 (6f0=1+2+36() (7)f(t)=tcos(at) (8)f()=e"+m-1 (2)F(s)=sin(ax+)=sin ax coso+cosarsinol aFo=iea-ml=c-ael=,ta4n产afa 4F=-=-e1=4 1 asa(s+a)ss+a） Fe)=P1=rreh=-rk=-号eg-子eg-子et-号 oF=4+2+3601=7++3 ona-ameI-时e4-o-网*orol品 1 s2-a2 (8)Fs)=5e"+at-1 1 142求下列各函数的原函数： )+s+3到 252+16 32+9+9 (s+2)(s+4) (2g+5s+6+12 s2+3s+2 (G+35+2 解：(1)设F(s)的部分分式展开为

第 14 章 线性动态电路的复频域分析 14-1 求下列各函数的像函数： at f t e − (1) ( ) = 1 − (2) f (t) = sin(t + ) (3) f (t) e (1 at) at = − − (1 ) 1 (4) ( ) at e a f t − = − 2 (5) f (t) = t (6) f (t) = t + 2 + 3δ(t) (7) f (t) = t cos(at) (8) ( ) = + − 1 − f t e at at 解: (1) ( ) [1 ] at F s e − =  − ( ) 1 1 s s a a s s a + = + = − (2)F(s) = [sin(t + )] = [sint cos + costsin] 2 2 2 2 2 2 cos sin cos sin          + + = + + + = s s s s s (3)F(s) [e (1 at)] at = − −  [ ] at at e ate − − =  − 2 2 ( ) ( ) 1 s a s s a a s a + = + − + = (1 )] 1 (4) ( ) [ at e a F s − =  − ] 1 1 [ at e a a − =  − ( ) 1 ( ) 1 1 as a s a s s + a = + = − (5) ( ) = [ ] = 2 F s  t t e dt st   − = 0 2 st t de s −   = − 0 1 2 −  −  −  = − 0 − 2 0 − 3 0 2 st 2 st 2 st te s te s e s t 3 2 s = (6)F(s) = [t + 2 + 3 (t)] 3 1 2 2 = + + s s (7)F(s) = [t cos(at)] ( )] 2 1 [ j t j t t e e    − = + ] ( ) 1 ( ) 1 [ 2 1 2 2 s ja s + ja + − = 2 2 2 2 2 (s a ) s a + − = (8) ( ) = [ + − 1] − F s e at at  s s a s a 1 1 2 + − + = ( ) 2 2 s s a a + = 14-2 求下列各函数的原函数： ( 2)( 4) ( 1)( 3) (1) + + + + s s s s s ( 5 6)( 12) 2 16 (2) 2 2 + + + + s s s s 3 2 2 9 9 (3) 2 2 + + + + s s s s s s s s ( 3 2) (4) 2 3 + + 解：（1）设 F(s) 的部分分式展开为

F回)=+5+).人+K:+K s(s+2)(s+4) +2++4 K,F 则待定系数为K,=(s+2)F一=4 K=lc+4FGl一号 所以，原函数为 0=0+2e*+3c) 2因为F-a+2*西-车+4名+车品 2s2+16 则待定系数为 k=c+3Fo-号 a 所以，有f0=是e”-。*+1是em 5 9 45 （3》因为F6=2+9灯+9=2+ 35+5 s2+3s+2 235+2 设F(d)为 =07产车+车 35+5 则待定系数为 k=c+ol-t2-2 K2=s+2)F(s川2= 35+5, 5+221 所以，原函数为f)=28)+2e+e 3 52 35+2 （④)因为F6)=G+35+2s=g子+35+21G+iW5+习

( 2)( 4) ( 1)( 3) ( ) + + + + = s s s s s F s 2 4 1 2 3 + + + = + s K s K s K 则待定系数为 8 3 [( 4) ( )] 4 1 [( 2) ( )] 8 3 [ ( )] 3 4 2 2 1 0 = + = = + = = = =− =− = s s s K s F s K s F s K sF s 所以，原函数为 (3 2 3 ) 8 1 ( ) 3t 4t f t e e − − = + + （2）因为 ( 2)( 3)( 12) 2 16 ( ) 2 + + + + = s s s s F s 2 3 12 1 2 3 + + + + + = s K s K s K 则待定系数为 45 152 [( 12) ( )] 9 34 [( 3) ( )] 5 12 [( 2) ( )] 3 12 2 3 1 2 = + = = + = − = + = =− =− =− s s s K s F s K s F s K s F s 所以，有 t t t f t e e e 2 3 12 45 152 9 34 5 12 ( ) − − − = − + （3）因为 3 2 2 9 9 ( ) 2 2 + + + + = s s s s F s 3 2 3 5 2 2 + + = + s s s 设 ( ) 1 F s 为 3 2 3 5 ( ) 1 2 + + + = s s s F s ( 1)( 2) 3 5 + + + = s s s 1 2 1 2 + + + = s K s K 则待定系数为 1 2 3 5 [( 2) ( )] 2 2 3 5 [( 1) ( )] 2 1 2 2 1 1 1 1 = + + = + = = + + = + = =− =− =− =− s s s s s s K s F s s s K s F s 所以，原函数为 t t f t t e e 2 ( ) 2 ( ) 2 − − =  + + （4）因为 s s s s F s ( 3 2) ( ) 2 3 + + = ( 1)( 2) 3 2 1 3 2 2 2 + + + − + + = s s s s s s

设FS)为 3g+2 F(s)= (+105+2)s+1+2 则代定系数为 ,=5+0Fs=3s+2 5+2=-1 =5+2F6=3+2 所以，原函数为f)=)+e‘-4e 14-3求下列各函数的原函数： 1 (1) +1 (5+10s+2)2 ②+2+2 3)产+6s+5 s(s2+4s+5 ④G+1 解：(1)令D(s)=0,有P=-1为单根，P2=-2为二重根，所以，设发F9s)为 r0=a+W2点+号+o 1 用6+2乘以F刊得+2F)=,中 则代定系数为 k-+F()(2-1 k=- kagr 所以，原函数为f)=e-e-1e S+1 +1 《2)因为F)+2x+2G2+25+2D0 令Ds)=0有A=0为单根，A=-1+LP2=-1-1为共轭复根，所以，设 F)=+ K2+ K3 s5+1-js+1+1 则各系数为

设 ( ) 1 F s 为 ( 1)( 2) 3 2 ( ) 1 + + + = s s s F s 1 2 1 2 + + + = s K s K 则代定系数为 4 1 3 2 [( 2) ( )] 1 2 3 2 [( 1) ( )] 2 1 2 2 1 1 1 1 = + + = + = = − + + = + = =− =− =− =− s s s s s s K s F s s s K s F s 所以，原函数为 t t f t δ t e e 2 ( ) ( ) 4 − − = + − 14-3 求下列各函数的原函数： (1) 2 ( 1)( 2) 1 s + s + (2) s s s s 2 2 1 3 2 + + + (3) ( 4 5) 6 5 2 2 + + + + s s s s s (4) 2 2 (s + 1) s 解： （1）令 D(s) = 0, 有 p1 = −1 为单根， p2 = −2 为二重根，所以，设发 F9s) 为 2 1 22 21 2 ( 1)( 2) 1 2 ( 2) 1 ( ) + + + + + = + + = s K s K s K s s F s 用 2 (s + 2) 乘以 F(s) 得 1 1 ( 2) ( ) 2 + + = s s F s 则代定系数为 1 1 1 1 1 1 1 ( 2) 1 [( 1) ( )] 22 2 21 2 1 1 2 1 = − + = = − + = = + = + = =− =− =− =− s s s s ds s d K s K s K s F s 所以，原函数为 t t t f t e e te 2 2 ( ) − − − = − − （2）因为 ( ) 1 ( 2 2) 1 2 2 1 ( ) 3 2 2 D s s s s s s s s s s F s + = + + + = + + + = 令 D(s)=0 有 p1 = 0 为单根 , p1 = −1+ j1, p2 = −1− j1 为共轭复根，所以，设 1 1 1 ( ) 1 2 3 s j K s j K s K F s + + + + − = + 则各系数为

lF(05 k-28w云p03 s+1 K,=Ke4=03536en 所以，原函数为f)=0.5+0.707ecos1-135) (3)令D)=0有乃=0为单根，P2=-2+1P,=-2-1为共轭复根，设 F(s)= 产+65-+2-n+2* K2 K s2+45+5)3 则各系数为 k.-tru 人器n护等 K=Kke网=e5 所以，原函数为f)=1+2esnt （4因为F)=G++产s-)D) 令Ds)=0,有P=-j和P2=j分别为二重根，且P,和P2为共轭复根，故设 K. 则各系数为 =s+n“an-分-e K=Kk=e9-月 Ka=4【s+Fs-1=0 K2=0 所以，原函数为f0=J分e”-e=2sn1 144 图(a),(b),(c)所示电路原己达到稳态，=0时把开关S合上，分别画出运算电路

0 2 0 2 135 3 2 135 2 2 1 1 1 0 2 0 0.3536 0.3536 3 4 2 1 ( ) ( ) 0.5 2 2 1 [ ( )] j j j s p s j s s K K e e e s s s D s N s K s s s K sF s = = = + + + =  = = + + + = = − − = =− + = =  所以，原函数为 ( ) 0.5 0.707 cos( 135 ) 0 = + − − f t e t t (3)令 D(s) = 0 有 p1 = 0 为单根， p2 = −2 + j1, p3 = −2 − j1 为共轭复根，设 ( 4 5) 2 1 2 1 6 5 ( ) 1 2 3 2 2 s j K s j K s K s s s s s F s + + + + − = + + + + + = 则各系数为 2 3 2 2 2 2 1 2 2 2 0 2 1 0 2 2 3 8 5 6 5 ( ) ( ) 1 4 5 6 5 [ ( )]    j j j s p s j s s K K e e j e s s s s D s N s K s s s s K sF s = = = − = + + + + =  = = + + + + = = − − = =− + = = 所以，原函数为 f t e t t ( ) 1 2 sin −2 = + （4）因为 ( 1) ( ) ( ) ( ) ( ) 2 2 2 2 D s s s j s j s s s F s = + − = + = 令 D(s) = 0 , 有 p = − j 1 和 p = j 2 分别为二重根， 且 1 p 和 2 p 为共轭复根，故设 s j K s j K s j K s j K F s − + + + − + + = 12 22 2 21 2 11 ( ) ( ) ( ) 则各系数为 0 [( ) ( )] 0 4 1 4 1 4 1 4 1 ( ) [( ) ( )] 22 1 2 12 2 21 11 2 2 1 2 11 1 1 1 = = + = = = = − = = − = + = =− − − = =− K s j F s ds d K K K e e j j e s j s K s j F s s j j j s p s    所以，原函数为 f t j te j te t t jt jt sin 2 1 4 1 4 1 ( ) = − = − 14-4 图（a） ，（b）, (c) 所示电路原已达到稳态，t=0 时把开关 S 合上，分别画出运算电路

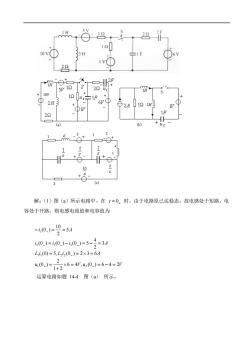
12 )6 1v① 2 12u 2H 6- 92A121H 1 22 1 10 (e) 解：(1)图()所示电路中，在t=0时，由于电路原已达稳态，故电感处于短路，电 容处于开路，则电感电流值和电容值为 40.)=40.)-40.)=5-1=31 L44(0)=5,L4(0.)=2×3=6A %0.1-26=40)=6-4=2r 运算电路如题14-4图(a)所示

解：（1）图（a）所示电路中，在 = 0− t 时，由于电路原已达稳态，故电感处于短路，电 容处于开路，则电感电流值和电容值为 u V u V L i L i A i i i A i A 6 4 , (0 ) 6 4 2 1 2 2 (0 ) (0) 5, (0 ) 2 3 6 3 2 4 (0 ) (0 ) (0 ) 5 5 2 10 (0 ) 1 2 1 1 2 2 2 1 3 1  = = − = + = = =  = = − = − = − = = − − − − − − − 运算电路如题 14-4 图（a） 所示

m-O 1 0b) ( (2)图(b)所示电路中，在1=0时，电路己达稳态，电感处于短路，电容处于开路， 电感电流值和电容电压值为 1(0.)=2(0)=2A,c(0)=0 故运算电路如题解14-4图(6)所示 (3)图(c)所示电路中，在1=0.时，电路己稳态，电感处于短路，电容处于开路，电 感电流值和电容电压值为 10 40.)=40.)3+1+2A 502 40.)=%0.1-号x0=24 运算电路如题解14-4图(c)所示。 14-5 图示电路原处于零状态，1=0时合上开关S,试求电流1，。 ①50 1.33H 100 题135图 解：由于开关闭合前电路已处于零状态，故有i,(0)=0,山c(0)=0,可画出该电路的 运算电路如题图14-5所示

（2）图（b）所示电路中，在 = 0− t 时，电路已达稳态，电感处于短路，电容处于开路， 电感电流值和电容电压值为 i 1 (0− ) = i 2 (0− ) = 2A,uC (0− ) = 0 故运算电路如题解 14-4 图 (b) 所示 （3）图（c）所示电路中，在 = 0− t 时，电路已稳态，电感处于短路，电容处于开路，电 感电流值和电容电压值为 u u A i i A 10 2 5 2 2 1 (0 ) (0 ) 2 3 1 1 10 (0 ) (0 ) 1 2 1 2 = =   = = + + = = − − − − 50 运算电路如题解 14-4 图（c）所示。 14-5 图示电路原处于零状态 ， t = 0 时合上开关 S ，试求电流 L i 。 解 ：由于开关闭合前电路已处于零状态，故有 i L (0− ) = 0,uC (0− ) = 0 ，可画出该电路的 运算电路如题图 14-5 所示

i() sL sC 题135图 应用回路电流法，设回路电流为1，(s),1,(),方向如图所示，可列出方程 ++,(- +R+2Lo-9 解得 50 1(5)=1()LC 1 代入以知数据，得 7500 7500 1.=S+20s+750)s06+50X5+150 -115 0.5 ；5+50+5+150 求其反变换得i,)=5[U,(s】=0-1.5e5+0.5e1s0)A 14-6 电路如图所示，己知i,0_)=0A,t=0,时将开关S闭合，求P0时的4z(0。 49 +xs ①10ev4a 解：图示电路中，己知，(0)-0A，可画出该电路的运算电路如题14-6图所示 采用接点电压法。设参考结点电压，对结点)可列出方程 1020(s sL

应用回路电流法，设回路电流为 ( ) 1 I s ， ( ) 2 I s ， 方向如图所示，可列出方程 s I s sC RI s R s R sL I s RI s 50 ) ( ) 1 ( ) ( 50 ( ) ( ) ( ) 1 2 1 2 + + = + + = 解得 ) 1 1 ( 50 1 ( ) ( ) 2 1 LC s RC s s RLC I s I s L + + = = 代入以知数据，得 ( 50)( 150) 7500 ( 200 7500) 7500 ( ) 2 + + = + + = s s s s s s I s L 150 0.5 50 1 1.5 + + + = − s s s 求其反变换得 i t I s e e A t t L l ( ) [ ( )] (1 1.5 0.5 ) −1 −50 −150 =  = − + 14-6 电路如图所示，已知 iL (0− ) = 0A,t = 0 ，时将开关 S 闭合，求 t>0 时的 u (t) L 。 解：图示电路中，已知 i L (0− ) − 0A ，可画出该电路的运算电路如题 14-6 图所示。 采用接点电压法。设参考结点电压，对结点(1) 可列出方程 sL U s s R U s R R sL 2 ( ) ( 1) 10 ) ( ) 1 1 1 ( 1 1 1 1 2 − + + + =

代入己知数据并整理，得 兮+3w-2+ 5 解的 5s U,(s)= (s+1(3+6) 故有 00=o=。品品。 15s 其反变换为4，(s)=5-lU,(s=(-3e'+18e)W 本题亦可采用网孔电流法求解 241 + ① 恶解3-6图 14-7 电路如图，设电容上原有电压Uc。=100Ψ电源电压，=200Ψ， R=302,R=102,L=0.1H,C=1000F。求S合上电感中的电流i,0) R U(s) 题13-13图 解：开关S同合前电路已达稳态，有元0，)一0-5A 且已知c(0.)=Uc=100,则该电路的运算电路如题解 14-13图所示。 采用结点电压求解。设参考结点如图所示，对结点(1)列方程

代入已知数据并整理，得 2( 1) 5 ) ( ) 3 2 1 ( 1 + + = s U s s 解的 ( 1)( 6) 5 ( ) 1 + + = s s s U s 故有 6 18 1 3 ( 1)( 6) 15 ( ) 3 ( ) 1 + + + − = + + = = s s s s s U s U s L 其反变换为 u s U s e e V t t L L ( ) [ ( )] ( 3 18 ) −1 − −6 =  = − + 本题亦可采用网孔电流法求解 14-7 电路如图，设电容上原有电压 UC0 = 100V 电源电压 Us = 200V , R1 = 30,R2 =10,L = 0.1H,C =1000F 。求 S 合上电感中的电流 i (t) L 。 解：开关 S 闭合前电路已达稳态，有 i L 5A 40 200 (0− ) = = 且已知 uC (0− ) = UC0 =100V ，则该电路的运算电路如题解 14-13 图所示。 采用结点电压求解。设参考结点如图所示，对结点(1) 列方程

Li.(o 1(s) 12(s) sC' 题解3-13图 200+0.5 《+2*龙*cw.o=克-c四 代入已知参数值并解得 Un6=2x10-25x105-10x s(3+200)2 所以，有 200+0.5-U.(95s2+700s+40000 1(s)= R+sL s(s+200)2 子+0 z(0=5-'[Uz(s月=5+1500e-20w 14-8 图示电路中的储能元件均为零初始值，4，()=58(P,在下列条件下求U1(S) (1)r=-3:(2)r=3n 12 12 解：图示电路中，由于储能元件均处于零状态，故该电路的运算电路如题解14-14图 所示

( s sC R sL s sC U s R sL R n 100 0.5 200 ) ( ) 1 1 ( 1 1 1 2 − + + + + = + 代入已知参数值并解得 2 6 3 2 1 ( 200) 2 10 25 10 100 ( ) +  −  − = s s s s U s n 所以，有 t L L n L i t I s t e s s s s s s R sL U s s I s 1 200 2 2 2 1 1 ( ) [ ( )] 5 1500 ( 200) 5 1500 ( 200) 5( 700 40000) 0.5 ( ) 200 ( ) − − = = + + = + + + + = + + − =  14-8 图示电路中的储能元件均为零初始值， us (t) = 5(t)V ，在下列条件下求 U1(S) (1)r = −3;(2)r = 3 。 r i1 us 1F 解：图示电路中，由于储能元件均处于零状态，故该电路的运算电路如题解 14-14 图 所示

题解3-14图 应用结点电压法。参考结点选取如图所示，结点电压U(s)既为U,(S),对结点可 列出结点(1)电压方程为 5 rI (s) 0,(5)= 1 2 1+ 1+ 1 1 4=产5-O6+ 5 其中 1+* s(2s+1) 将式(2)代入到方程式(1)中，得 U,(s)= 5(2-rs+1)2 s2-r)(s+1)2+6s2+5s+1川 (1)当r=-3时，有 25(s+1)2 25(s+1)2 U0=01e+153+6is2+55+6 i3+T (2)当r=3时，得 U,6)=二55+-.-6+2 s2(5s+3) 6+房 14-9 图示电路中，i=2sim(10001)4,R=R,=202C=1000F,1=0时合上开关，用运算法 求Uc()

应用结点电压法。参考结点选取如图所示，结点电压 ( ) 1 U s n 既为 ( ) 1 U s ，对结点 可 列出结点（1）电压方程为 2 ( ) s 1 1 1 1 5 ( ) 2 1 1 1 1 s 1 1 1 1 1 1 1 rI s s U s s − + + =                 + + + + + 其中 (2 1) [5 ( )]( 1) 1 1 ( ) 5 ( ) 1 1 1 + − + = + + − = s s sU s s s s U s s I s 将式（2）代入到方程式（1）中，得 [(2 )( 1) 6 5 1] 5(2 )( 1) ( ) 2 2 2 1 − + + + + − + = s r s s s r s U s （1）当 r = −3 时，有 ) 11 6 11 15 ( ( 1) 11 25 (11 15 6) 25( 1) ( ) 2 2 2 2 1 + + + = + + + = s s s s s s s U s （2）当 r = 3 时，得 ) 5 3 ( ( 1) (5 3) 5( 1) ( ) 2 2 2 2 1 + + = − + − + = s s s s s s U s 14-9 图示电路中， i s = 2sin(1000t)A，R1 = R2 = 20,C =1000F,t = 0 时合上开关，用运算法 求 U (t) C