《电路》课程教学资源（A）习题解答_第2章 电阻电路的等效变换

第2章电阻电路的等效变换 21 电路如图所示，已知4，=100V,R=2k2,R=8k2。若：(1)R=8k2:(2) R3=o(R处开路)：(3)R3=0(R处短路)。试求以上3种情况下电压，和电流i,马。 R42 题2-1图 解：(1)R和R为并联，其等效电阻R-号=4kQ, 则总电流 元+R2-9m4 分流有 6=4,=号-0=8333mA 4=R4.=8×0=6667y (2)当R=o,有1，=0 6=R+R=298=10m4 42=R42=8×10=80V (3)R=0,有i2=0,4=0 4=是=罗9=50m4 2-2 电路如图所示，其中电阻、电压源和电流源均为已知，且为正值。求：(1)电压山和电 流2：(2)若电阻R增大，对哪些元件的电压、电流有影响？影响如何？

第 2 章 电阻电路的等效变换 2-1 电 路 如 图 所 示 ， 已 知 1 2 100 , 2 , 8 s u V R k R k = =  =  。 若 ：（ 1 ） 3 R k =  8 ；（ 2 ） R3 = (R3处开路） ；（3） R3 = 0(R3处短路） 。试求以上 3 种情况下电压 2 u 和电流 2 3 i i , 。 解：（1） R2 和 R3 为并联，其等效电阻 8 4 2 R k = =  ， 则总电流 mA R R u i s 3 50 2 4 100 1 1 = + = + = 分流有 mA i i i 8.333 6 50 2 1 2 = 3 = = = u R i 66.667 V 6 50 2 = 2 2 = 8 = （2）当 R3 =  ，有 i 3 = 0 mA R R u i s 10 2 8 100 1 2 2 = + = + = u2 = R2 i 2 = 810 = 80V （3） R3 = 0 ，有 i 2 = 0,u2 = 0 mA R u i s 50 2 100 1 3 = = = 2-2 电路如图所示，其中电阻、电压源和电流源均为已知，且为正值。求：（1）电压 2 u 和电 流 2 i ；（2）若电阻 R1 增大，对哪些元件的电压、电流有影响？影响如何？

题2-2园 解：(1)对于R和R来说，其余部分的电路可以用电流源1，等效代换，如题解图 (a)所示。因此有 R (2)由于R和电流源串接支路对其余电路来说可以等效为一个电流源，如题解图(b) 所示。因此当R增大，对R,R,R,及u,的电流和端电压都没有影响。 但R增大，R上的电压增大，将影响电流源两端的电压，因为 4,=R4+山2-4， 显然4，随R的增大而增大。 R42R3 2 (a) 6 2-3 电路如图所示，0)求兰：②)当及>R∥风仁足时，受可近似为风冬2 此时引起的相对误差为 。- R R+Rx100%

解：（1）对于 R2 和 R3 来说，其余部分的电路可以用电流源 s i 等效代换，如题解图 （a）所示。因此有 2 3 3 3 2 R R R i i + = 2 3 2 3 2 R R R R i u s + = （2）由于 R1 和电流源串接支路对其余电路来说可以等效为一个电流源，如题解图（b） 所示。因此当 R1 增大，对 2 3 4 R ,R ,R 及 s u 的电流和端电压都没有影响。 但 R1 增大， R1 上的电压增大，将影响电流源两端的电压，因为 s s s ui = R1 i + u2 − u 显然 s i u 随 R1 的增大而增大。 2-3 电路如图所示。（1）求 s o u u ；（2）当 // ( ) 1 2 1 2 1 2 R R R R RL R R +  = 时， s o u u 可近似为 1 2 2 R R R + ， 此时引起的相对误差为 0 0 1 2 2 100 + − s o s o u u R R R u u

当R为(R∥R)的100倍、10倍时，分别计算此相对误差。 恶2-3图 解：)R-是 所以告-风是RF尼+及提+民R R2RL ②)设风=水指入上述受式子中，可得 尼K R“a灯*R是记 相对误差为 R、 KR、 R 。(台-RR)x100%1+KR+R,R+Rx100% 。 K u. 1+KR+R K -×100%=-×10% 1+K 当K=100时 n=-1% K=10时 n=-10%

当 RL 为 ( // ) R1 R2 的 100 倍、10 倍时，分别计算此相对误差。 解：（1） L L R R R R R +  = 2 2 R R u i s + = 1 R R u R u Ri s o + = = 1 所以 L L L s o R R R R R R R R R R R u u 1 2 1 2 2 1 + + = + = （2）设 1 2 1 2 R R R R RL K + = ，带入上述 s o u u 式子中，可得 1 2 2 1 2 1 2 1 2 1 2 1 2 1 2 2 (1 ) ( ) R R R K K R R R R R R R R K R R R R R K u u s o +  + = + + +  +  = 相对误差为 0 0 0 0 0 0 1 2 2 1 2 2 1 2 2 0 0 1 2 2 100 1 100 1 1 1 100 1 1 ( ) 100  = −  + − + =  + + + − + + =  + − = K K K K K R R R K K R R R R R R K K u u R R R u u s o s o  当 K =100 时 0 0  = −1 K =10 时 0 0  = −10

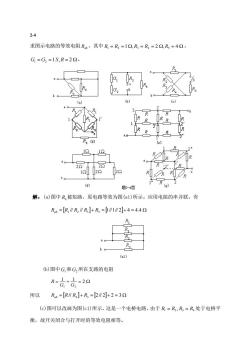
2-4 求图示电路的等效电阻Rs,其中R=R=12,R=R=22,R=42, G=G2=1S,R=22. G2 b o (b) 尺 46 RR 3' R R (d) 80 201 R2R 2 题2-4图 解：(a)图中R,被短路，原电路等效为图(al)所示。应用电阻的串并联，有 R=[R∥R∥R]+R=W1M2]+4=4.42 (6)图中G,和G,所在支路的电阻 R=G+G=29 所以Rb=[R∥R]+R=2∥2]+2=32 (c)图可以改画为图(C1)所示，这是一个电桥电路，由于R=R2,R=R处于电桥平 衡，故开关闭合与打开时的等效电阻相等

2-4 求图示电路的等效电阻 Rab ，其中 R1 = R2 =1,R3 = R4 = 2 ,R5 = 4  ， G1 = G2 =1 S,R = 2 。 解：(a)图中 R4 被短路，原电路等效为图(a1)所示。应用电阻的串并联，有 Rab = R1 // R2 // R3 + R5 = 1//1// 2+ 4 = 4.4  (b)图中 G1 和 G2 所在支路的电阻 = + = 2  1 1 G1 G2 R 所以 Rab = R// R4 + R3 = 2// 2+ 2 = 3  (c)图可以改画为图(c1)所示，这是一个电桥电路，由于 1 2 3 4 R = R ,R = R 处于电桥平 衡，故开关闭合与打开时的等效电阻相等

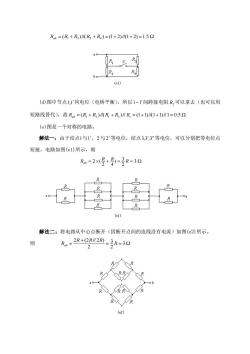
R=(R+R)R2+R)=(1+2)1+2)=1.52 R s R R ) ()图中节点1，'同电位（电桥平衡），所以1-'间跨接电阻R可以拿去（也可以用 短路线替代)，故R=(R+R)MR+R)∥R=(1+1)1+)∥1=0.52 (e)图是一个对称的电路。 解法一：由于结点1与'，2与2等电位，结点3,3,3”等电位，可以分别把等电位点 短接，电路如图(el)所示，则 R=2x(5+)=2R=30 解法二：将电路从中心点断开（因断开点间的连线没有电流）如图(2)所示。 则 R=2R+2,R/2R=号R=30 2 RR

Rab = (R1 + R3 )//(R2 + R4 ) = (1+ 2)//(1+ 2) =1.5  (d)图中节点 1,1 同电位（电桥平衡），所以 1−1 间跨接电阻 R2 可以拿去（也可以用 短路线替代），故 Rab = (R1 + R2 )//(R1 + R2 )// R1 = (1+1)//(1+1)//1 = 0.5  (e)图是一个对称的电路。 解法一：由于结点 1 与 1，2 与 2 等电位，结点 3,3 ,3 等电位，可以分别把等电位点 短接，电路如图(e1)所示，则 =  + = = 3  2 3 ) 2 4 2 ( R R R Rab 解法二：将电路从中心点断开（因断开点间的连线没有电流）如图(e2)所示。 则 = =  + = 3 2 3 2 2 (2 // 2 ) R R R R Rab

解法三：此题也可根据网络结构的特点，令各支路电流如图(3)所示，则左上角的 网孔回路方程为 2B2=2R, 故 2= 由结点①的KCL方程 0.5i=2+i1=22=21 得 4== 由此得端口电压4=R×0.5i+2R×i+R×0.5i=号R 所以 R=告=R=3Q R (e3) (f)图中(12,12,22)和(22,22,12)构成两个Y形连接，分别将两个Y形转化成等 值的△形连接，如图(f1)和(f2)所示。 等值△形的电阻分别为 R=1+1+1)=2.50 R=1+2+1×2)=52 R=R=52 R=2+2+2x2=80 5=1+2+1×2=42 R=R=42 并接两个△形，最后得图(3)所示的等效电路，所以 R=[2IlR∥R)+R∥R]IR∥R) =[25∥4)+2.518]5∥4) -[20,4020-1269n 19+2i"9

解法三：此题也可根据网络结构的特点，令各支路电流如图(e3)所示，则左上角的 网孔回路方程为 2Ri2 = 2Ri1 故 2 1 i = i 由结点①的 KCL 方程 5 2 1 2 2 2 1 0. i = i + i = i = i 得 i i i 4 1 2 = 1 = 由此得端口电压 u R i R i R i Ri ab 2 3 0.5 4 1 =  0.5 + 2  +  = 所以 = = = 3  2 3 R i u R ab ab (f)图中 (1 ,1 , 2 )    和 (2 , 2 ,1 )    构成两个 Y 形连接，分别将两个 Y 形转化成等 值的△形连接，如图(f1)和(f2)所示。 等值△形的电阻分别为 =   =  =    = + + =   = =   = + + =   =  = + +  = + + 4 4 2 1 2 1 2 8 1 2 2 5 2 2 ) 5 1 1 2 ) 2.5 (1 2 2 1 1 (1 1 2 3 2 3 2 1 1 2 R R R R R R R R 并接两个  形，最后得图(f3)所示的等效电路，所以     2 2 1 1 3 3 2 //( // ) // //( // ) 2 //(5// 4) 2.5// 8 //(5// 4) 20 40 20 // 1.269 19 21 9 R R R R R R R ab = +    = +   = + =     

R∥RR∥R2Q (3) (g)图是一个对称电路。 解法一：由对称性可知，节点1，1"等电位，节点2,2,2“等电位，连接等电位点，得 图(g1)所示电路。则 Rb=(号+8+)=2R=1.6672 e4) (e2) 解法二：根据电路的结构特点，得各支路电流的分布如图(g2)所示。由此得端口电 压 s=}×R+名×R+ixR=名xR 所以Rs=-名R=1.67Q 注：本题入端电阻的计算过程说明，判别电路中电阻的串并联关系是分析混联电路的关键。一 般应掌握以下几点 (1)根据电压、电流关系判断。若流经两电阻的电流是同一电流，则为串联：若两电阻上承受 的是同一电压，就是并联。注意不要被电路中的一些短接线所迷惑，对短接线可以做压缩或伸长处

(g)图是一个对称电路。 解法一：由对称性可知，节点 1,1 ,1 等电位，节点 2,2 ,2 等电位，连接等电位点，得 图(g1)所示电路。则 = + + = = 1.667  6 5 ) 3 6 3 ( R R R R Rab 解法二：根据电路的结构特点，得各支路电流的分布如图(g2)所示。由此得端口电 压 uab = i  R + i  R + i  R = i  R 6 5 3 1 6 1 3 1 所以 = = = 1.667  6 5 R i u R ab ab 注：本题入端电阻的计算过程说明，判别电路中电阻的串并联关系是分析混联电路的关键。一 般应掌握以下几点 （1）根据电压、电流关系判断。若流经两电阻的电流是同一电流，则为串联；若两电阻上承受 的是同一电压，就是并联。注意不要被电路中的一些短接线所迷惑，对短接线可以做压缩或伸长处

理。 (2)根据电路的结构特点，如对称性、电桥平衡等，找出等电位点，连接或断开等电位点之间 的支路，把电路变换成荷单的并联形式。 (3)应用Y,△结构互换把电路转化成简单的串并联形式，再加以计算分析。但要明确，Y,△ 形结构互换是多端子结构等效，除正确使用变换公式计算各阻值之外，务必正确连接各对应端子， 更应注意不要把本是串并联的问题看做Y,△结构进行变换等效，那样会使问题的计算更加复杂化。 (4)当电路结构比较复杂时，可以根据电路的结构特点，设定电路中的支路电流，通过一些网 孔回路方程和结点方程确定支路电流分布系数，然后求出断口电压和电流的比值，得出等效电阻。 2-7 在图(a)电路中，41=24V,42=6,R=122,R=62,R=22。图(6)为经电源变 换后的等效电路。 (a) 题2-5图 b) (1)求等效电路的1，和R (2)根据等效电路求R,中电流和消耗功率： (3)分别在图(a),(b)中求出RR,及R消耗的功率： (4)试问山，4发出的功率是否等于1，发出的功率？R,R,消耗的功率是否等于R消耗 的功率？为什么？ 解：(1)利用电源的等效变换，图()中电阻与电压源的串联可以用电阻与电流源 的并联来等效。等效后的电路如题解2-5图所示，其中 a=是=没=24 a-觉-8-14 对题解2-5图电路进一步简化得图（⑥）所示电路，故

理。 （2）根据电路的结构特点，如对称性、电桥平衡等，找出等电位点，连接或断开等电位点之间 的支路，把电路变换成简单的并联形式。 （3）应用 Y， 结构互换把电路转化成简单的串并联形式，再加以计算分析。但要明确，Y， 形结构互换是多端子结构等效，除正确使用变换公式计算各阻值之外，务必正确连接各对应端子， 更应注意不要把本是串并联的问题看做 Y,  结构进行变换等效，那样会使问题的计算更加复杂化。 （4）当电路结构比较复杂时，可以根据电路的结构特点，设定电路中的支路电流，通过一些网 孔回路方程和结点方程确定支路电流分布系数，然后求出断口电压和电流的比值，得出等效电阻。 2-7 在图(a)电路中， us1 = 24V,us2 = 6V,R1 =12 ,R2 = 6 ,R3 = 2  。图(b)为经电源变 换后的等效电路。 （1）求等效电路的 s i 和 R ； （2）根据等效电路求 R3 中电流和消耗功率； （3）分别在图(a),(b)中求出 R1, R2 及 R 消耗的功率； （4）试问 1 2 , us us 发出的功率是否等于 s i 发出的功率？ 1 2 R ,R 消耗的功率是否等于 R 消耗 的功率？为什么？ 解：（1）利用电源的等效变换，图(a)中电阻与电压源的串联可以用电阻与电流源 的并联来等效。等效后的电路如题解 2-5 图所示，其中 A R u i s s 2 12 24 1 1 1 = = = A R u i s s 1 6 6 2 2 2 = = = 对题解 2-5 图电路进一步简化得图(b)所示电路，故

1=1+i2=2+1=3A R=R风-8=40 (2)由图(6)可解得三条并联支路的端电压 u=(R∥R)x,=经x3=4W 所以R,的电流和消耗的功率分别为 6=-是=2A P=R3=2x22=8W (3)根据KWL,图(a)电路中R,R,两端的电压分别为 4=41-u=24-4-20y 42=42-=6-4=2V 则R,R消耗的功率分别为 月-发g933w (6)图中R消耗的功率 P=发=号=4 (4)(a)图中u,和u,2发出的功率分别为 尺=×费-24×8=0W Pa=a×瓷=6x名=2m (6)图中1，发出功率卫=×1，=4×3=12W 显然 P≠P+P 由(3)的解可知 P≠P+E 以上结果表明，等效电源发出的功率一般并不等于原电路中所有电源发出的功率 之和：等效电阻消耗的功率一般也并不等于原电路中所有电阻消耗的功率之和。这充分

i s = i s1 + i s2 = 2 +1 = 3 A =  +  = = 4 12 6 12 6 // R R1 R2 （2）由图(b)可解得三条并联支路的端电压 u R R i s 3 4 V 4 2 4 2 ( // ) 3  = +  =  = 所以 R3 的电流和消耗的功率分别为 P R i W A R u i 2 2 8 2 2 4 2 2 3 3 3 3 3 = =  = = = = （3）根据 KVL，图(a)电路中 1 2 R ,R 两端的电压分别为 u u u V u u u V s s 6 4 2 24 4 20 2 2 1 1 = − = − = = − = − = 则 1 2 R ,R 消耗的功率分别为 W R u P W R u P 3 2 6 (2) 33.33 3 100 12 (20) 2 2 2 2 2 2 1 2 1 1 = = = = = = (b)图中 R 消耗的功率 W R u P 4 4 4 2 2 = = = （4）(a)图中 us1和us2 发出的功率分别为 W R u P us s u 40 12 20 24 1 1 1 1 =  =  = W R u P us s u 2 6 2 6 2 2 2 2 =  =  = (b)图中 s i 发出功率 P u i s W s i =  = 43 =12 显然 1 s2 u s u s Pi  P + P 由（3）的解可知 P  P1 + P2 以上结果表明，等效电源发出的功率一般并不等于原电路中所有电源发出的功率 之和；等效电阻消耗的功率一般也并不等于原电路中所有电阻消耗的功率之和。这充分

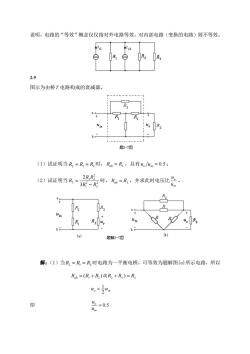
说明，电路的“等效”概念仅仅指对外电路等效，对内部电路（变换的电路）则不等效 2 e 风e 2-9 图示为由桥T电路构成的衰减器。 题2-7图 (1)试证明当R2=R=R,时，R=R,且有./um=0.5: (2）试证明当R,=3R-R 2RR 时，凡=R,并求此时电压比警。 R2 R R R“。 题解2-7图 ) 解：(1)当R=R=R,时电路为一平衡电桥，可等效为题解图()所示电路，所以 R=(R+R2)M(R2+R)=RL 4。=54 即 2-05

说明，电路的“等效”概念仅仅指对外电路等效，对内部电路（变换的电路）则不等效。 2-9 图示为由桥 T 电路构成的衰减器。 （1）试证明当 R2 = R1 = RL 时， Rab = RL ，且有 uo uin = 0.5 ； （2）试证明当 2 2 1 2 1 2 3 2 L L R R R R R − = 时， Rab = RL ，并求此时电压比 in o u u 。 解：（1）当 R2 = R1 = RL 时电路为一平衡电桥，可等效为题解图(a)所示电路，所以 Rab = R + R R + RL = RL ( )//( ) 1 2 2 uo uin 2 1 = 即 = 0.5 in o u u