《自动控制原理》课程教学资源（电子教案）梅逊公式

2.4控制系统的方块图、信号流图与梅逊公式控制系统的方块图是系统各元件特性、系统结构和信号流向的图解表示法。2.4.1方块图元素（1）方块（BlockDiagram）：表示输入到输出单向传输间的函数关系。r(t)c(t)g(s)R(s)+ c(s)4方块信号线图2-14方块图中的方块信号线：带有箭头的直线，箭头表示信号的流向，在直线旁标记信号的时间函数或象函数。（2）比较点（合成点、综合点）SummingPoint两个或两个以上的输入信号进行加减比较的元件，“+”表示相加，“”表示相减。“+”号可省略不写。T1T 1+T 2R(s)-R(s)R(s)++R(s)T 2T3T1Ｔ1-T2+T3T 2图2-15比较点示意图注意：进行相加减的量，必须具有相同的量刚。(3)分支点（引出点、测量点）BranchPoint表示信号测量或引出的位置32

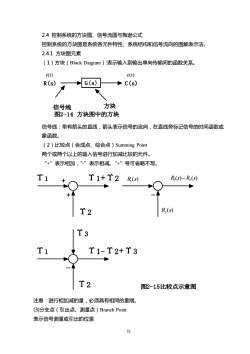
32 2.4 控制系统的方块图、信号流图与梅逊公式 控制系统的方块图是系统各元件特性、系统结构和信号流向的图解表示法。 2.4.1 方块图元素 （1）方块（Block Diagram）:表示输入到输出单向传输间的函数关系。 R(s) G(s) C(s) 图2-14 方块图中的方块 信号线 方块 r(t) c(t) 信号线：带有箭头的直线，箭头表示信号的流向，在直线旁标记信号的时间函数或 象函数。 （2）比较点（合成点、综合点）Summing Point 两个或两个以上的输入信号进行加减比较的元件。 “+”表示相加，“-”表示相减。“+”号可省略不写。 Υ + 1 Υ1+Υ2 Υ2 + - ( ) ( ) 1 2 R s −R s ( ) 1 R s ( ) 2 R s Υ1 Υ1-Υ2+Υ3 Υ2 - Υ3 图2-15比较点示意图 注意：进行相加减的量，必须具有相同的量刚。 (3)分支点（引出点、测量点）Branch Point 表示信号测量或引出的位置

c(s)R(s)P(s)G(s)G,(s)P(s)图2-16分支点示意图注意：同一位置引出的信号大小和性质完全一样。2.4.2几个基本概念及术语N(s)E(s)++R(s)G,(s)G;(s)B(s)H(s)打开反馈图2-17反馈控制系统方块图(1)前向通路传递函数假设N(s)=0打开反馈后，输出C(s)与R(s)之比。在图中等价于C(s)与误差E(s)之比C() = G(s)G,(s)=G(s)E(s)(2）反馈回路传递函数FeedforwardTransferFunction假设N(s)=0主反馈信号B（s)与输出信号C（s）之比B(s) = H(s)C(s)(3）开环传递函数Open-loopTransferFunction假设N(s)=0主反馈信号B(s)与误差信号E(s)之比。33

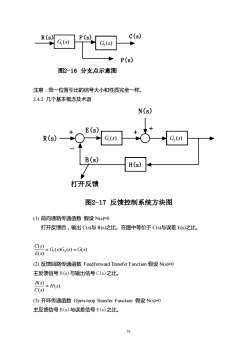
33 图2-16 分支点示意图 P(s) R(s) P(s) C(s) ( ) 1 G s ( ) 2 G s 注意：同一位置引出的信号大小和性质完全一样。 2.4.2 几个基本概念及术语 + + H(s) - + R(s) E(s) B(s) N(s) 打开反馈 ( ) 1 G s ( ) 2 G s 图2-17 反馈控制系统方块图 (1) 前向通路传递函数 假设 N(s)=0 打开反馈后，输出 C(s)与 R(s)之比。在图中等价于 C(s)与误差 E(s)之比。 ( ) ( ) ( ) ( ) ( ) 1 2 G s G s G s E s C s = = (2) 反馈回路传递函数 Feedforward Transfer Function 假设 N(s)=0 主反馈信号 B(s)与输出信号 C(s)之比。 ( ) ( ) ( ) H s C s B s = (3) 开环传递函数 Open-loop Transfer Function 假设 N(s)=0 主反馈信号 B(s)与误差信号 E(s)之比

B(=G(s)G;(s)H(s)=G()H(s)E(s)(4）闭环传递函数Closed-loopTransferFunction假设N(s)=0输出信号 C(s)与输入信号R(s)之比G(s)C(s) _G,(s)G,(s)R(s)1+H(s)G(s)1+ H(s)G(s)推导:因为C(s)=E(s)G(s)=[R(s)-C(s)H(s)G(s)G(s)右边移过来整理得 C(s)R(s)1+ H(s)G(s)G(s)即C(s)前向通路传递函数R(s)1+H(s)G(s)1+开环传递函数(5)误差传递函数假设N(s)=0误差信号E(s)与输入信号R(s)之比。将C(s)=E(s)G(s)代入上式，消去G(s)即得：11E(s)R(s)1+H(s)G(s)1+开环传递函数(6）输出对扰动的传递函数假设R(s)=0N(s)G,(s)C(s)H(s)G.CS图2-18输出对扰动的结构图G,(s)C(s)由图2-18，利用公式**，直接可得：Mx（s)N(s)1+G(s)H(s)（7）误差对扰动的传递函数假设R(s)=0G(s)H(s)N(s)★ E(s)G;(s)图2-19误差对扰动的结构图34

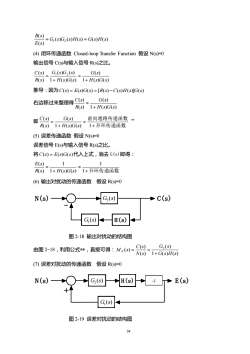
34 ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 2 G s G s H s G s H s E s B s = = (4) 闭环传递函数 Closed-loop Transfer Function 假设 N(s)=0 输出信号 C(s)与输入信号 R(s)之比。 1 ( ) ( ) ( ) 1 ( ) ( ) ( ) ( ) ( ) ( ) 1 2 H s G s G s H s G s G s G s R s C s + = + = 推导：因为 C(s) = E(s)G(s) = [R(s) −C(s)H(s)]G(s) 右边移过来整理得 1 ( ) ( ) ( ) ( ) ( ) H s G s G s R s C s + = 即 开环传递函数 前向通路传递函数 + = + = 1 ( ) ( ) 1 ( ) ( ) ( ) H s G s G s R s C s ** (5) 误差传递函数 假设 N(s)=0 误差信号 E(s)与输入信号 R(s)之比。 将 C(s) = E(s)G(s) 代入上式，消去 G(s)即得： +开环传递函数 = + = 1 1 1 ( ) ( ) 1 ( ) ( ) R s H s G s E s (6) 输出对扰动的传递函数 假设 R(s)=0 - N(s) C(s) H(s) ( ) 2 G s ( ) 1 G s 图 2-18 输出对扰动的结构图 由图 2-18，利用公式**，直接可得： 1 ( ) ( ) ( ) ( ) ( ) ( ) 2 G s H s G s N s C s M s N + = = (7) 误差对扰动的传递函数 假设 R(s)=0 N(s) H(s) E(s) ＋ ( ) 1 G s ( ) 2 G s -1 图 2-19 误差对扰动的结构图

由图2-19，利用公式**，直接可得：E(s) - -G,(s)H(s)M ne (s) =N(s)1+G(s)H(s)线性系统满足叠加原理，当控制输入R（s）与扰动N(s）同时作用于系统时，系统的输出及误差可表示为：G(s)G,(s)N(s)C(s)= 7R(s) +1+G(s)H(s)1+G(s)H(s)1G;(s)H() N(s)E(s) =R(s)-1+G(s)H(s)1+G(s)H(s)注意：由于N(s)极性的随机性，因而在求E(s)时，不能认为利用N(s)产生的误差可抵消R(s)产生的误差。2.4.3方块图的绘制（1）考虑负载效应分别列写系统各元部件的微分方程或传递函数，并将它们用方框（块）表示。（2）根据各元部件的信号流向，用信号线依次将各方块连接起来，便可得到系统的方块图。系统方块图-也是系统数学模型的一种。例2-8画出下列RC电路的方块图ROOu,uo1O(a)图2-20一阶RC网络解：由图2-20，利用基尔霍夫电压定律及电容元件特性可得：u, -u.[(s) - U()-U,(a)(1)RR对其进行拉氏变换得：[idt[U (s)= 1()(2)uosCc由（1）和（2）分别得到图（b）和(c）。35

35 由图 2-19，利用公式**，直接可得： 1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 G s H s G s H s N s E s M s NE + − = = 线性系统满足叠加原理，当控制输入 R(s)与扰动 N(s)同时作用于系统时，系统的 输出及误差可表示为： ( ) 1 ( ) ( ) ( ) ( ) 1 ( ) ( ) ( ) ( ) 2 N s G s H s G s R s G s H s G s C s + + + = ( ) 1 ( ) ( ) ( ) ( ) ( ) 1 ( ) ( ) 1 ( ) 2 N s G s H s G s H s R s G s H s E s + − + = 注意：由于 N(s)极性的随机性，因而在求 E(s)时，不能认为利用 N(s)产生的误差可抵 消 R(s)产生的误差。 2.4.3 方块图的绘制 （1）考虑负载效应分别列写系统各元部件的微分方程或传递函数，并将它们用方框（块） 表示。 （2）根据各元部件的信号流向，用信号线依次将各方块连接起来，便可得到系统的方 块图。 系统方块图-也是系统数学模型的一种。 例 2-8 画出下列 RC 电路的方块图。 R C i （a） ui uo 图 2-20 一阶 RC 网络 解：由图 2-20，利用基尔霍夫电压定律及电容元件特性可得：        = − =  c idt u R u u i o i o 对其进行拉氏变换得：      = − = (2) ( ) ( ) (1) ( ) ( ) ( ) sC I s U s R U s U s I s o i o 由（1）和（2）分别得到图（b）和(c)

U,(s)I(s)4C1I (s)U.(s)SCU.(s)(b)(c)将图（b）和（c)组合起来即得到图(d），图（d)为该一阶RC网络的方块图。U.(s)I (s)1U,(s)RSCU.(s)(d)例2-9画出下列R-C网络的方块图。R2R,ii,uC,C.u,O(a)电路图RR2Uc (s)O.中1U.(s)U,(s)sC2sC,I,(s),(s)O(b）运算电路图解：（1）根据电路定理列出方程，写出对应的拉氏变换，也可直接画出该电路的运算电路图如图(b）；（2）根据列出的4个式子作出对应的框图；（3）根据信号的流向将各方框依次连接起来。36

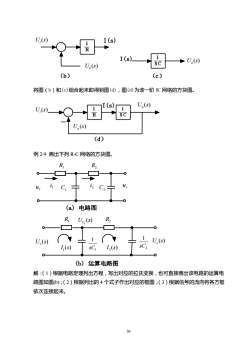
36 （b） Ui (s) I(s) U (s) o I(s) （c） U (s) o 将图（b）和(c)组合起来即得到图(d)，图(d)为该一阶 RC 网络的方块图。 － I(s) （d） U (s) o U (s) o U (s) i 例 2-9 画出下列 R-C 网络的方块图。 (a) 电路图 ur 1 i 2 i R1 R2 uc C1 C2 (b) 运算电路图 R1 ( ) R2 1 U s C U (s) r U (s) c ( ) 1 I s ( ) 2 I s 1 1 sC 2 1 sC 解：（1）根据电路定理列出方程，写出对应的拉氏变换，也可直接画出该电路的运算电 路图如图(b)；（2）根据列出的 4 个式子作出对应的框图；（3）根据信号的流向将各方框 依次连接起来

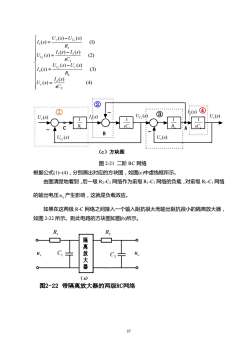
U,(s)-Uc (s)(1)I,(s)R,I,(s)-12(s)(2)Uc (s)=sC,Uc (s)-U,(s)(3)I,(s)R,I,(s)(4)U.(s)SC2②④?I(s)③Uc(s)U.(s)I(s)U,(s)RRSCsCC:Uc(s)U,(s)（c）方块图图2-21二阶RC网络根据公式(1)~(4），分别画出对应的方块图，如图(c)中虚线框所示由图清楚地看到，后一级R2-C2网络作为前级Ri-Ci网络的负载，对前级Ri-C网络的输出电压u。产生影响，这就是负载效应。如果在这两极R-C网络之间接入一个输入阻抗很大而输出阻抗很小的隔离放大器，如图2-22所示。则此电路的方块图如图(b)所示。R,R2隔离放大器OuruC(a)图2-22带隔离放大器的两级RC网络37

37              = − = − = − = (4) ( ) ( ) (3) ( ) ( ) ( ) (2) ( ) ( ) ( ) (1) ( ) ( ) ( ) 2 2 2 2 1 1 2 1 1 1 1 1 sC I s U s R U s U s I s sC I s I s U s R U s U s I s c C c C r C - - - C B ① ② ③ ④ A （c）方块图 1 1 sC 2 1 sC ( ) 1 U s C U (s) r ( ) 1 I s U (s) c U (s) c ( ) 2 I s 1 1 R 2 1 R ( ) 1 U s C 图 2-21 二阶 RC 网络 根据公式(1)~(4)，分别画出对应的方块图，如图(c)中虚线框所示。 由图清楚地看到，后一级 R2-C2 网络作为前级 R1-C1 网络的负载，对前级 R1-C1 网络 的输出电压 1 c u 产生影响，这就是负载效应。 如果在这两极 R-C 网络之间接入一个输入阻抗很大而输出阻抗很小的隔离放大器， 如图 2-22 所示。则此电路的方块图如图(b)所示。 图2-22 带隔离放大器的两级RC网络 隔 离 放 大 器 R1 R2 ur C1 C2 uc （ a）

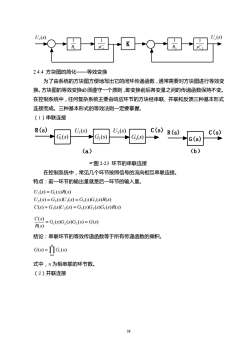
U.(S)U.(sTy1KTOIRTsC2.4.4方块图的简化一等效变换为了由系统的方块图方便地写出它的闭环传递函数，通常需要对方块图进行等效变换。方块图的等效变换必须遵守一个原则，即变换前后各变量之间的传递函数保持不变。在控制系统中，任何复杂系统主要由响应环节的方块经串联、并联和反馈三种基本形式连接而成。三种基本形式的等效法则一定要掌握。（1）串联连接R(s)C(s)U,(s)U,(s)R(s)c(s)G(s)G,(s)G,(s)G(s)(b)(a)图2-23环节的串联连接在控制系统中，常见几个环节按照信号的流向相互串联连接特点：前一环节的输出量就是后一环节的输入量。U,(s)=G,(s)R(s)U,(s)=G,(s)U,(s)=G,(s)G,(s)R(s)C(s) = G,(s)U,(s) = G,(s)G2(s)G,(s)R(s)C =G(s)G;(s)G;(s) =G(s)R(s)结论：串联环节的等效传递函数等于所有传递函数的乘积。G,(s)G(s)=式中，n为相串联的环节数。（2）并联连接38

38 K 1 1 R 2 1 1 R 1 sC 2 1 sC U (s) r U (s) c 2.4.4 方块图的简化——等效变换 为了由系统的方块图方便地写出它的闭环传递函数，通常需要对方块图进行等效变 换。方块图的等效变换必须遵守一个原则，即变换前后各变量之间的传递函数保持不变。 在控制系统中，任何复杂系统主要由响应环节的方块经串联、并联和反馈三种基本形式 连接而成。三种基本形式的等效法则一定要掌握。 （1）串联连接 R(s) C(s) （a） ( ) 1 U s ( ) 2 U s ( ) 1 G s ( ) 2 G s ( ) 3 G s R(s) G(s) C(s) （b） 图 2-23 环节的串联连接 在控制系统中，常见几个环节按照信号的流向相互串联连接。 特点：前一环节的输出量就是后一环节的输入量。 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 3 2 3 2 1 2 2 1 2 1 1 1 C s G s U s G s G s G s R s U s G s U s G s G s R s U s G s R s = = = = = ( ) ( ) ( ) ( ) ( ) ( ) 1 2 3 G s G s G s G s R s C s = = 结论：串联环节的等效传递函数等于所有传递函数的乘积。 = = n i i G s G s 1 ( ) ( ) 式中，n 为相串联的环节数。 （2）并联连接

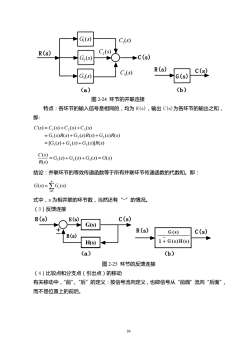
G;(s)C(s)C,(s)R(s)C(s)G,(s)R(s)c(s)C,(s)G;(s)G(s)(b)(a)图2-24环节的并联连接特点：各环节的输入信号是相同的，均为R（s），输出C(s)为各环节的输出之和，即：C(s) = C,(s) +C,(s)+C,(s)= G,(s)R(s)+G,(s)R(s)+G,(s)R(s)=[G,(s) +G,(s) +G,(s)]R(s)C =G(s)+G,(s)+G,()= G(s)R(s)结论：并联环节的等效传递函数等于所有并联环节传递函数的代数和。即：G(s)=≥G()1=1式中，n为相并联的环节数，当然还有"_”的情况。（3）反馈连接R(s)c(s)E(s)G(s)R(s)Xc(s)G(s)B(s)1 + G(s)H(s)H(s)(a)(b)图2-25环节的反馈连接（4）比较点和分支点（引出点）的移动有关移动中，“前"、“后”的定义：按信号流向定义，也即信号从“前面”流向“后面”而不是位置上的前后。39

39 （a） R(s) ( ) C(s) 2 G s ( ) 1 G s ( ) 3 G s ( ) 2 C s ( ) 1 C s ( ) 3 C s G(s) （b） R(s) C(s) 图 2-24 环节的并联连接 特点：各环节的输入信号是相同的，均为 R(s)，输出 C(s)为各环节的输出之和， 即: [ ( ) ( ) ( )] ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 2 3 1 2 3 1 2 3 G s G s G s R s G s R s G s R s G s R s C s C s C s C s = + + = + + = + + ( ) ( ) ( ) ( ) ( ) ( ) 1 2 3 G s G s G s G s R s C s = + + = 结论：并联环节的等效传递函数等于所有并联环节传递函数的代数和。即： ( ) ( ) 1 G s G s n i  i = = 式中，n 为相并联的环节数，当然还有“-”的情况。 （3）反馈连接 （a） R(s) C(s) G(s) H(s) ＋－ E(s) B(s) （b） R(s) C(s) 图 2-25 环节的反馈连接 （4）比较点和分支点（引出点）的移动 有关移动中，“前”、“后”的定义：按信号流向定义，也即信号从“前面”流向“后面”， 而不是位置上的前后

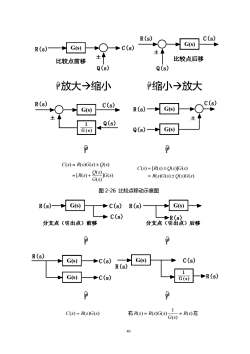
R(s)C(s)G(s)G(s)C(s)R(s)±土比较点后移比较点前移Q(s)Q(s)放大>缩小缩小→放大C(s)R(s)c(s)G(s)R(s)G(s)土土Q(s)1G(s)Q(s)G(s)EeC(s) = R(s)G(s)±Q(s)C(s) =[R(s)±Q(s)]G(s)g(s)G(s)=[R(s)+ = R(s)G(s)±Q(s)G(s)G(s)图2-26比较点移动示意图G(s)R(s)R(s)c(s)G(s)c(s)福r(s)分支点（引出点）前移分支点（引出点）后移ER(s)G(s)c(s)G(s)>C(s)R(s)1>R(s)G(s)→C(s)G(s)E右R(s)= R(s)G(s)=R(s)左C(s) = R(s)G(s)G(s)40

40 R(s) C(s) ＋ G(s) Q(s) 比较点前移 比较点后移 R(s) C(s) G(s) ＋ Q(s) 放大→缩小 缩小→放大 G(s) R(s) C(s) G(s) ＋ Q(s) C(s) R(s) G(s) G(s) ＋ Q(s)   ] ( ) ( ) ( ) [ ( ) ( ) ( ) ( ) ( ) G s G s Q s R s C s R s G s Q s = + =  ( ) ( ) ( ) ( ) ( ) [ ( ) ( )] ( ) R s G s Q s G s C s R s Q s G s =  =  图 2-26 比较点移动示意图 R(s) 分支点（引出点）前移 G(s) C(s) C(s) 分支点（引出点）后移 R(s) G(s) R(s)   C(s) C(s) R(s) G(s) G(s) C(s) R(s) G(s) R(s)   C(s) = R(s)G(s) 右 ( ) ( ) 1 ( ) ( ) ( ) R s G s R s = R s G s = 左

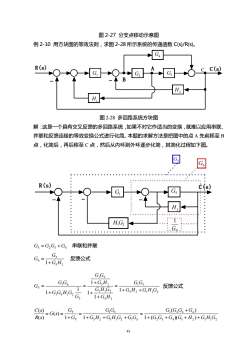
图2-27分支点移动示意图例2-10用方块图的等效法则，求图2-28所示系统的传递函数C(s)/R(s)。G.R(s)C(s)AG,GBH,H.图2-28多回路系统方块图解·这是一个具有交叉反馈的多回路系统，如果不对它作适当的变换，就难以应用串联并联和反馈连接的等效变换公式进行化简。本题的求解方法是把图中的点A先前移至B点，化简后，再后移至C点，然后从内环到外环逐步化简，其简化过程如下图。回GR(s)c(s)GH,G,串联和并联G, =G,G, +G4Gs反馈公式G=1+G,H,G,GsG,G1+G,H,G,GsG,反馈公式G,H,G,1+G,H, +G,H,G,1+.1+G,G,H,G,G1+G,H2G,G,GsC(s)G,(G,G, +G)=G(s)=R(s)1+G,1+G,H, +G,H,G, +G,G,1+(G,G, +G,)(G, +H,)+G,H,G,41

41 图 2-27 分支点移动示意图 例 2-10 用方块图的等效法则，求图 2-28 所示系统的传递函数 C(s)/R(s)。 R(s) A - B C(s) G1 G2 G3 G4 H1 H2 - C 图 2-28 多回路系统方块图 解：这是一个具有交叉反馈的多回路系统，如果不对它作适当的变换，就难以应用串联、 并联和反馈连接的等效变换公式进行化简。本题的求解方法是把图中的点 A 先前移至 B 点，化简后，再后移至 C 点，然后从内环到外环逐步化简，其简化过程如下图。 R(s) - - - C(s) G1 H2 G5 G6 G7 H1G2 5 1 G G5 = G2G3 + G4 串联和并联 5 2 5 6 1 G H G G + = 反馈公式 5 2 1 1 2 1 5 5 2 1 1 2 5 2 1 5 5 1 6 1 2 1 6 7 1 1 1 1 1 1 G H G H G G G G H G H G G H G G G G G H G G G G + + = + + + = + = 反馈公式 2 3 4 1 2 1 1 2 1 2 3 4 5 2 1 1 2 1 5 1 5 7 7 1 ( )( ) ( ) 1 1 ( ) ( ) ( ) G G G G H G H G G G G G G H G H G G G G G G G G s R s C s + + + + + = + + + = + = =