《自动控制原理》课程教学资源（电子教案）第五章 线性系统的频域分析法（2/2）

第5章线性系统的频域分析法Frequency-responseanalysis5.1频率特性及其表示法幅相曲线对数频率特性曲线5.2典型环节对数频率特性曲线的绘制5.3典型环节的幅相曲线的绘制5.4稳定裕度和判据5.2典型环节对数频率特性曲线的绘制5.2.5最小相位系统与非最小相位系统Minimum phasesystems andnon-minimumphasesystems在右半s平面内既无极点也无零点的传递函数，称为最小相位传递函数；反之，在右半s平面内有极点和（或）零点的传递函数，称为非最小相位传递函数。具有最小相位传递函数的系统称为最小相位系统，反之，具有非最小相位传递函数的系统，称为非最小相位系统在具有相同幅值特性的系统中，最小相位传递函数（系统）的相角范围，在所有这类系统中是最小的。任何非最小相位传递函数的相角范围，都大于最小相位传递函数的相角范围。118

118 第 5 章 线性系统的频域分析法 Frequency-response analysis 5.1 频率特性及其表示法 幅相曲线 对数频率特性曲线 5.2 典型环节对数频率特性曲线的绘制 5.3 典型环节的幅相曲线的绘制 5.4 稳定裕度和判据 5.2 典型环节对数频率特性曲线的绘制 5.2.5 最小相位系统与非最小相位系统 Minimum phase systems and non-minimum phase systems 在右半 s 平面内既无极点也无零点的传递函数，称为最小相位传递 函数；反之，在右半 s 平面内有极点和（或）零点的传递函数，称为非 最小相位传递函数。具有最小相位传递函数的系统称为最小相位系统， 反之，具有非最小相位传递函数的系统，称为非最小相位系统。 在具有相同幅值特性的系统中，最小相位传递函数（系统）的相角 范围，在所有这类系统中是最小的。任何非最小相位传递函数的相角范 围，都大于最小相位传递函数的相角范围

对于最小相位系统，其传递函数由单一的幅值曲线唯一确定。对于非最小相位系统则不是这种情况作为例子，考虑下列两个系统，它们的特性频率分别为：1+ joT1- joTG(jo) :, G2(jo)=0<T<T1+ joT,1+joTjo jo a??O111.1TTTiT图5-18最小相位系统和非最小相位系统的零-极点分布图如前所述，对于最小相位系统，幅值特性和相角特性之间具有唯一的对应关系。这意味着，如果系统的幅值曲线在从零到无穷大的全部频率范围上给定，则相角曲线被唯一确定，反之亦然。这个结论对于非最小相位系统不成立。119

119 对于最小相位系统，其传递函数由单一的幅值曲线唯一确定。对于 非最小相位系统则不是这种情况。 作为例子，考虑下列两个系统，它们的特性频率分别为： 1 1 1 1 ( ) j T j T G j    + + = ， 1 1 2 , 0 1 1 ( ) T T j T j T G j   + − =    jω σ T 1 − 1 1 T − 1 1 T − jω σ T 1 图 5-18 最小相位系统和非最小相位系统的零-极点分布图 如前所述，对于最小相位系统，幅值特性和相角特性之间具有唯一的对应 关系。这意味着，如果系统的幅值曲线在从零到无穷大的全部频率范围上 给定，则相角曲线被唯一确定，反之亦然。这个结论对于非最小相位系统 不成立

BodeDiagram-5(ap)apnubee-10-15-2045(bap) ased-90-13518010°10210110'10Frequency (rad/sec)图5-19G;(s)和G(s)的相角特性G,(jの)G2(jの)0-20-40-60-80-100-120-140-160-18010210°10210110'120

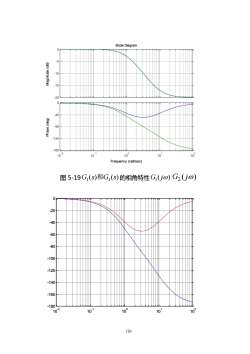
120 Bode Diagram Frequency (rad/sec) Phase (deg) Magnitude (dB) -20 -15 -10 - 5 0 10 - 2 10 - 1 10 0 10 1 10 2 -180 -135 -90 -45 0 图 5-19 ( ) ( ) 1 1 G s 和G s 的相角特性 ( ) G1 j ( ) G2 j 10-2 10-1 100 101 102 -180 -160 -140 -120 -100 -80 -60 -40 -20 0

图 5-19G;(s)和Gi(s)的相角特性对于最小相位系统，相角在の=00时变为-90(n-m)dB /dec，n为极点数，m为零点数。两个系统的对数幅值曲线在の=00时的斜率都等于-20(n-m)dB/dec。因此，为了确定系统是不是最小相位的既需要检查对数幅值曲线高频渐近线的斜率，又需检查在の=00时相角。如果当の=00时对数幅值曲线的斜率为-20(n-m)dB/dec，并且相角等于一90°（n－m)dB/dec，那么该系统就是最小相位系统5.2.6传递延迟(Transport lag)Seep190传递延时是一种非最小相位特性。如果不采取对消措施，高频时将造成严重的相位滞后。这类传递延迟通常存在于热力、液压和气动系统中。延迟环节的输入和输出的时域表达式为c(t) = l(t - t)r(t - t)C(s)=e-s G(jo)=e-jotG(s) =R(s)其幅值总是等于1。这是因为[G(jo)=cosot- jsin ot=1因此，传递延迟的对数幅值等于0分贝。传递延迟的相角为121

121 图 5-19 ( ) ( ) 1 1 G s 和G s 的相角特性 对于最小相位系统，相角在  =  时变为− 90(n − m)dB / dec ，n 为 极点数，m 为零点数。两个系统的对数幅值曲线在  =  时的斜率都等 于 − 20(n − m)dB / dec 。因此，为了确定系统是不是最小相位的既需要检 查对数幅值曲线高频渐近线的斜率，又需检查在  =  时相角。如果当  =  时对数幅值曲线的斜率为− 20(n − m)dB / dec ，并且相角等于 − 90(n − m)dB / dec ，那么该系统就是最小相位系统。 5.2.6 传递延迟(Transport lag)See p190 传递延时是一种非最小相位特性。如果不采取对消措施，高频时将造成严 重的相位滞后。这类传递延迟通常存在于热力、液压和气动系统中。 延迟环节的输入和输出的时域表达式为 c(t) = 1(t − )r(t − ) s e R s C s G s − = = ( ) ( ) ( )   j G j e − ( ) = 其幅值总是等于 1。这是因为 G( j) = cos − jsin  =1 因此，传递延迟的对数幅值等于 0 分贝。传递延迟的相角为

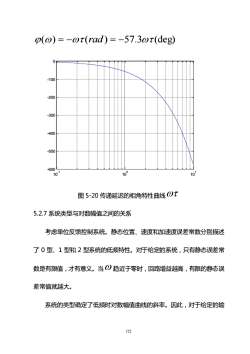
p(の) = -のt(rad) = -57.3ot(deg).-100-200-300-400-500-6001010°10图5-20传递延迟的相角特性曲线QT5.2.7系统类型与对数幅值之间的关系考虑单位反馈控制系统。静态位置、速度和加速度误差常数分别描述了0型、1型和2型系统的低频特性。对于给定的系统，只有静态误差常数是有限值，才有意义。当の趋近于零时，回路增益越高，有限的静态误差常值就越大。系统的类型确定了低频时对数幅值曲线的斜率。因此，对于给定的输122

122 () = − (rad) = −57.3 (deg) 10-1 100 101 -600 -500 -400 -300 -200 -100 0 图 5-20 传递延迟的相角特性曲线  5.2.7 系统类型与对数幅值之间的关系 考虑单位反馈控制系统。静态位置、速度和加速度误差常数分别描述 了 0 型、1 型和 2 型系统的低频特性。对于给定的系统，只有静态误差常 数是有限值，才有意义。当  趋近于零时，回路增益越高，有限的静态误 差常值就越大。 系统的类型确定了低频时对数幅值曲线的斜率。因此，对于给定的输

入信号，控制系统是否存在稳态误差，以及稳态误差的大小，都可以从观察对数幅值曲线的低频区特性予以确定。①静态位置误差常数的确定E(s)R(s) +C(s)G(s)图5-21单位反馈控制系统考虑图5-21所示的单位反馈控制系统。假设系统的开环传递函数为K(Ts+1)(T2s + 1)..(Tms+ I)G(s) =s'(Tis + 1)(T2s+ 1)..(Tn-vs + 1)K(T j@+1)(T j@ +1)..(Tm j@ +1)G(jo) :(jの)(Tjの+1)(T2j0 +1)..(Tn-vjの+1)图5-22为一个0型系统对数幅值曲线的例子。在这个系统中，G(jo)在低频段等于K，即lim G(jo)= Kp0-0由此得知，低频渐近线是一条幅值为20logKp分贝的水平线。15G(s) =(s + 1)(0.2s + 1)123

123 入信号，控制系统是否存在稳态误差，以及稳态误差的大小，都可以从观 察对数幅值曲线的低频区特性予以确定。 静态位置误差常数的确定 + - R(s) E(s) C(s) G(s) 图 5-21 单位反馈控制系统 考虑图 5-21 所示的单位反馈控制系统。假设系统的开环传递函数为 ( 1)( 1) ( 1) ( 1)( 1) ( 1) ( ) 1 2 1 2 + + + + + + = − s T s T s T s K T s T s T s G s n m     ( ) ( 1)( 1) ( 1) ( 1)( 1) ( 1) ( ) 1 2 1 2 + + + + + + =    −        j T j T j T j K T j T j T j G j n m   图 5-22 为一个 0 型系统对数幅值曲线的例子。 在这个系统中， G( j) 在低频段等于 K p ，即 Kp G j = → lim ( ) 0   由此得知，低频渐近线是一条幅值为 K p 20log 分贝的水平线。 ( 1)(0.2 1) 15 ( ) + + = s s G s

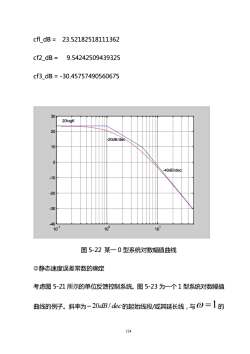
cfl_dB=23.52182518111362cf2 dB =9.54242509439325cf3dB=-30.457574905606753020logk20-20dB/dec100-40dB/dec-10-20-30-4010°10~110图5-22某一0型系统对数幅值曲线②静态速度误差常数的确定考虑图5-21所示的单位反馈控制系统。图5-23为一个1型系统对数幅值曲线的例子。斜率为-20dB/dec的起始线段/或其延长线，与の=1 的124

124 cfl_dB = 23.52182518111362 cf2_dB = 9.54242509439325 cf3_dB = -30.45757490560675 10-1 100 101 -40 -30 -20 -10 0 10 20 30 20logK -20dB/dec -40dB/dec 图 5-22 某一 0 型系统对数幅值曲线 静态速度误差常数的确定 考虑图 5-21 所示的单位反馈控制系统。图 5-23 为一个 1 型系统对数幅值 曲线的例子。斜率为−20dB/ dec 的起始线段/或其延长线，与  =1 的

直线的交点具有的幅值为20logK，。这可证明如下：K在 1 型系统中G(jの)=0<<1jo=20logK，斜率为-20dB/dec的起始线段/或其因此20log0=延长线与0 分贝线的交点的频率在数值上等于K，。假设交点上的频率为K01,于是即joK作为一个例子，考虑具有单位反馈的1型系统，其开环传递函数为：KG(s) =s(Ts + 1)如果定义转角频率为の2，假设斜率为－40dB/dec的直线与/或其延长线1K20302,0 =K, = K与0分贝线的交点为の3TT由此得到 2 =01_03即302在伯德图上, log O1 - log 0 = log 03 -log 2125

125 直线的交点具有的幅值为 Kv 20log 。这可证明如下： 在 1 型系统中 ( ) = ,  1   j K G j v 因此 v v K j K 20log 20log 1 1 =  =  斜率为 −20dB/ dec 的起始线段/或其 延长线与 0 分贝线的交点的频率在数值上等于 Kv 。假设交点上的频率为 1 ，于是 1 1 = j Kv 即 Kv =1 作为一个例子，考虑具有单位反馈的 1 型系统，其开环传递函数为： ( 1) ( ) + = s Ts K G s 如果定义转角频率为 2 ，假设斜率为−40dB/ dec 的直线与/或其延长线 与 0 分贝线的交点为 3 ， T 1 2 = ， T K = 2 3 ，1 = Kv = K 由此得到 2 1 2 =3 即 2 3 3 1     = 在伯德图上， 1 3 3 2 log −log = log −log

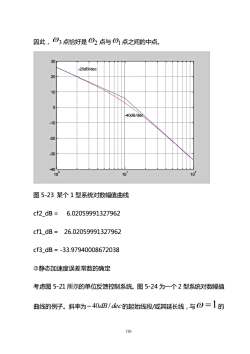
因此，①3点恰好是2点与01点之间的中点。30-20dB/dec20100-40dB/dee-10-20-30-401001010图5-23某个1型系统对数幅值曲线cf2_dB =6.02059991327962cf1 dB=26.02059991327962cf3_dB=-33.97940008672038③静态加速度误差常数的确定考虑图5-21所示的单位反馈控制系统。图5-24为一个2型系统对数幅值曲线的例子。斜率为-40dB/dec的起始线段/或其延长线，与の=1 的126

126 因此， 3 点恰好是 2 点与 1 点之间的中点。 100 101 102 -40 -30 -20 -10 0 10 20 30 -20dB/dec -40dB/dec 图 5-23 某个 1 型系统对数幅值曲线 cf2_dB = 6.02059991327962 cf1_dB = 26.02059991327962 cf3_dB = -33.97940008672038 静态加速度误差常数的确定 考虑图 5-21 所示的单位反馈控制系统。图 5-24 为一个 2 型系统对数幅值 曲线的例子。斜率为−40dB/ dec 的起始线段/或其延长线，与  =1 的

直线的交点具有的幅值为20logK。Ka0<<1G(io)由于低频时(jo)?K20log= 20log K所以(jo)斜率为－40dB/dec的起始线段/或其延长线与0分贝线的交点的频率为のa在数值上等于 K。α的平方根。证明如下：K.20log1=0于是=/K20log(joa)dB A-40dB/dec-60dB/dec-20dB/decの（对数坐标）C00a=Ka0=1图5-242型系统对数幅值曲线5.3极坐标图(Polarplot)，幅相频率特性曲线，奈奎斯特曲线G(jo)G(jの)可用幅值和相角 (の)的向量表频率特性是复数。127

127 直线的交点具有的幅值为 Ka 20log 。 由于低频时 , 1 ( ) ( ) 2 =     j K G j a 所以 a a K j K 20log ( ) 20log 1 2 = =  斜率为 −40dB/ dec 的起始线段/或其延长线与 0 分贝线的交点的频率为 a 在数值上等于 Ka 的平方根。证明如下： 20log1 0 ( ) 20log 2 = = a a j K  于是 a = Ka  ( 对数坐标 ) dB −40dB/dec −60dB/dec −20dB/dec  =1 0 a = Ka 图 5-24 2 型系统对数幅值曲线 5.3 极坐标图(Polar plot)，幅相频率特性曲线，奈奎斯特曲线 频率特性是复数。 G( j) 可用幅值 G( j) 和相角 () 的向量表