《自动控制原理》课程教学资源（作业习题）课后部分习题和答案

2-10设系统传递函数为2C(s)R(s)2+3s+2且初始条件c(0)=-1,c(0)=0。试求阶跃输入r（t)=1(t)时，系统的输出响应c（t)。解：由系统的传递函数得：d°c( +3 dc(0) +2c(t) =2r()(1)dt?dt对式（1）取拉氏变换得：s2C(s) - Sc(0) -c(0) +3sC(s) -3c(0)+2C(s)=2R(s)(2)将初始条件代入（2）式得(s* +3$ +2)(s) +$ +3 =2)s122-s2-3s22s +64即: C(s)=ss2+3s+2S+2s(s + 3s +2)$+1s所以：c(t)=2-4e-+2e-2r2-12求图2-61所示有源网络的传递函数RU1CR,(a)RUU-K93-KU(b)(c)图2-61有源网络1RoCosR.1解：（a）Z。=R/lT= RCo1Tos+1CasRo+Cos

U()--R--R(Tos+1)RoU,(s)Zo1RoCosRo1(b)Z= R IlT= R.Co1CasTos+1Ro+CosT,s +11Z, = R +T, = R,CC,sCis1ZU.(s)(Ts +I)(Tos +I)-ZoR.C,sU,(s)/15+11=R1Z/2 = R, (R, +C,sC,sT,s+1(c)C.sR,(T,s+ I)T, = R,C2二R+15+1T,s+R, +1C2sU.(s)Z12R,T,s+1U,(s)RoR T,s+R +12-17已知控制系统结构图如图2-65所示。试通过结构图等效变换求系统传递函数C(s)/R(s)。HG,()GsGAS(s)G()H)G,(s)H)(a)(d)G(8)HHOGGA)G(s)H()(b)GF(e)HOH(0H(O)G(s)G,(s)(c)GAs)(f)图2-65题2-17系统结构图

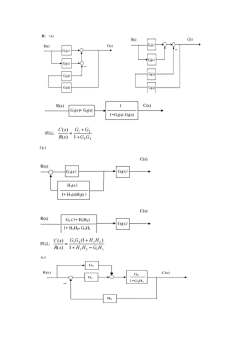
解：(a)R(s)C(s)G;(s)R(s)C(s)GsG(sG2(s)G(SG;(s)GalsC(s)R(s)1G(s)+ G(s)1+G2(s) G(s)C(s)G, +G,所以：R(s)1+G,G,(b)C(s)R(s)G(s)Gi(s)H(s)1+ Hi(s)H2(s)C(s)R(s)G (1+ H,H2)G(s)1+ H,H2- G,HiC(s)G,G,(I+H,H,)所以：R(s)I+H,H,-GH(c)R(s)C(s)G21+G2Hi

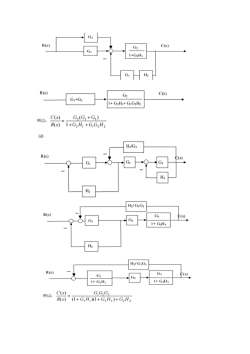
R(s)C(s)G21+G2H1R(s)C(s)G2G;+G31+G2H,+G,G2H2C(s)G(G,+G,)所以：R(s)1+G,H, +G,G,H2(d)H2/GR(s)(SGHH2H2/ G,G3R(s)G3C(s)G1+GH3H2H2/ G,G3R(s)G3C(s)GiG21+ G,H31+ G,H,C(s)G,G,G所以：R(s)(I+G,H)I+G,H)+G,H

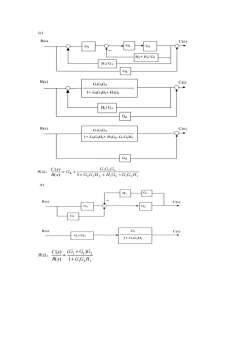
(e)R(s)C(s)H2+H/G3H/G334R(s)C(s)GG2G31+ G2G3H2+ H,G2H,/G3G4R(s)C(s)G,GG1+ G2G;H2+ H,G2- G,G2H1GaG,G,G3C(s)所以：=G.+R(s)1+G,G,H,+H,G,-G,G,H,(f)HiR(s)C(s)GTR(s)G2C(s)G,+G1+G,G2H;C(s)(G, +G,)G,所以：R(s)1+G,G,H

3-9设控制系统如图3-44所示。要求：rt)c(o)10s(s+1)（1）取1=0，t2=0.1，计算测速反馈校正系统的超调量、调节时间和速度误差：(2）取t1=01，T2=0，计算比例-微分校正系统的超调量、调节时间和速度误差。解：（1）系统开环传递函数10on10s(s + 1)10(1+ t,s)G(s) =(1 + t,s)10t,ss(s+1)+10t,ss(s + 2)S(s+250.)1+s(s + 1)1O,=/100=10250,=25=J100% = e-/- =35.1%3.5 = 3.5st,=EO.Kv =53-12已知系统特征方程如下，试求系统在s右半平面的根数及虚根值。s+3s+12s+24s2+32s+48=0(1)56+4s54s4+453-7s2-85+10=0(2)5s+3s4+1253+205+35s+25=0(3)解：（1）列劳思表如下：5613-4-71011232ss44-8543244854-5-510534165352124852S'si5oso有一对虚根，系统不稳定（2）列劳思表如下：系统不稳定

（3）列劳思表如下：5s1123554320251680s3352525st105o25有一对虚根，系统不稳定3-13已知单位反馈系统的开环传递函数K(0.5s +1)G(s) =s(s +1)(0.5s2 +$+1)试确定系统稳定时的K值范围。解：系统特征方程为s(s +1)(0.5s2 + s+1)+ K(0.5s +1) =0将上述方程化简得到：0.5s*+1.5s*+2s2+(1+0.5K)s+K=0劳思表如下：540.52K531.51+0.5K2.5-0.25Ks2K1.52.5-1.25K-0.125K2s2.50.25KsoK3-15已知单位反馈系统的开环传递函数100(1)G(s)=(0. Is + 1)(s + 5)50(2)G(s)= -s(0.1s + D(s + 5)10(2s +1)(3)G(s)=s(s2+6s+100)

试求输入分别为r(t)=2t和r(t)=2+2t+t时，系统的稳态误差。解：（1）因为是二阶系统，且系数大于零，所以系统稳定。K, = lims°G(s)= 0K, = limG(s) =20K,=limsG(s)=05-010-0R2=00所以当r(0)=2t时essKyRRR当r(0)=2+2+12=80es=i+K,K,"K.（2）应先检查系统的稳定性。K,=limG(s)=00Kv=limsG(s)=10Ka=lims"G(s)=0R2=0.2所以当r0=2t时esx:KyR,+R+R当r(0)=2+2t+12=8ex1+K.K.Ky（3）应先检查系统的稳定性。K, =limG(s) =00K,=lim sG(s)=00Ka=limsG(s)=0.1R2=0所以当r(0)=2t时essKyR,+R+R当r(0)=2+2+12=20es1+K,KaKy4-4设单位反馈控制系统开环传递函数如下，试概略绘出相应的闭环根轨迹图（要求确定分离点坐标d)：K(1)G(s) =s(0.2s +1)(0.5s +1)解：K10K系统开环传递函数为G(s=s(s+5)(s+2)s(s+5)(s+2)有三个极点：（0+j0），（-2+j0），（-5+j0）没有零点。分离点坐标计算如下：1一13d2+14d+10=0解方程的d,=-3.7863，d，=-0.88=0dd+2d+5取分离点为d=-0.88根轨迹如图中红线所示

K(s +1)(2)G(s)=s(2s + 1)K/2(s+I)K,(s+I)系统开环传递函数为G(s)=s(s+ 0.5)s(s+0.5)解：有两个极点：（0+j0），（一0.5+j0），有个零点（一1+j0）。分离点坐标计算如下：一11d2+2d+0.5=0解方程的d,=-1.7，d,=-0.29dd+0.5d+1取分离点为d，=-1.7，d,=-0.29根轨迹如图中红线所示。K'(s+5)(3)G(s)=s(s +2)(s + 3)解：K'(s+ 5)系统开环传递函数为G(s)=s(s + 2)(s + 3)有三个极点：（0+j0），（-2+j0），（-2+j0），有一个零点（-5+j0）。分离点坐标计算如下：1111d3+10d2+25d+15=0解方程的d=-6.5171d+3d+5dd+2

d,=-2.5964，d,=-0.8865取分离点为d=-0.8865根轨迹如图中红线所示。C4-6设单位反馈控制系统的开环传递函数如下，要求：K(1)确定G(s)=产生纯虚根的开环增益值。s(s +I(s +10)解：系统特征方程为s*+11s2+10s+K=0令s=jo代入特征方程中得：实部方程为：-1102=0虚部方程为：100-0=0解上述方程得：02=10K=110开环增益按一般定义：K=K'/10=11K'(s+=)(2)产生纯虚根为土j1的z值和K值。确定G(s)=s (s+10)(s +20)解：系统特征方程为s+30s*+200s2+Ks+K==0令s=j1代入特征方程中得：实部方程为：K=+1-200=0虚部方程为：K"-30=0解上述方程得：K"=30z=199/30