《自动控制原理》课程教学资源（PPT课件）第四章 线性控制系统的动静态分析

线性控制系统的动静态分析?3.1引言：3.2测试输入信号与时域性能指标3.3一阶系统的时域分析：3.4二阶系统的时域分析：3.5高阶系统的时域分析3.6稳态误差分析：3.7基本控制规律的时域分析

线性控制系统的动静态分析 ❖ 3.1 引言 ❖ 3.2 测试输入信号与时域性能指标 ❖ 3.3 一阶系统的时域分析 ❖ 3.4 二阶系统的时域分析 ❖ 3.5 高阶系统的时域分析 ❖ 3.6 稳态误差分析 ❖ 3.7 基本控制规律的时域分析

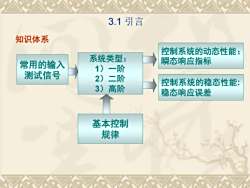
3.1引言知识体系控制系统的动态性能：系统类型：瞬态响应指标常用的输入1）一阶测试信号2）二阶控制系统的稳态性能：高阶3）稳态响应误差基本控制规律

3.1 引言 控制系统的动态性能： 系统类型： 瞬态响应指标 1）一阶 2）二阶 3）高阶 基本控制 规律 控制系统的稳态性能: 稳态响应误差 常用的输入 测试信号 知识体系

时域分析法：自动控制系统最基本的分析方法，是学习复域法、频域法的基础。可以直接在时间域中对系统进行分析校正，具有直观准确的特点。可以提供系统时间响应的全部信息基于解析法求解系统的输出，所以比较烦琐。一般是先求取控制系统的闭环传递函数和测试输入信号的拉普拉斯变换，借助拉普拉斯反变换获得系统输出的时域响应，然后对所获得的响应结果进行时域分析

时域分析法： ❖ 自动控制系统最基本的分析方法，是学习复域法、频域 法的基础。 ❖ 可以直接在时间域中对系统进行分析校正，具有直观， 准确的特点。 ❖ 可以提供系统时间响应的全部信息。 ❖ 基于解析法求解系统的输出，所以比较烦琐。 ❖ 一般是先求取控制系统的闭环传递函数和测试输入信号 的拉普拉斯变换，借助拉普拉斯反变换获得系统输出的 时域响应，然后对所获得的响应结果进行时域分析

3.2测试输入信号与时域性能指标常用测试输入信号3.2.11测试输入信号，输入系统，测试系统性能文方便数学上的分析和处理便于实际物理系统的测试，此时要求测试输入信号应易于通过实验仪器产生。常用测试输入信号>常用测试信号：R(s)r(t)e测试输入信号。单位阶跃函数和单位脉冲函数在初始时刻的速度均为无穷大8(t)1s单位脉冲函数函数，前者的新稳态为1，而1(t).1/se单位阶跃函数后者无新稳态。单位阶跃函数是理想的测试信号，但其初始ts1 /s2单位斜坡函数时刻之后速度为零，因此不适t2.2/s3,单位抛物线函数合用来测试系统跟随速度变化的输入信号的能力。n! / sn+1tn.一般形式

3.2 测试输入信号与时域性能指标 ❖ 测试输入信号，输入系统，测试系统性能 •方便数学上的分析和处理； •便于实际物理系统的测试，此时要求测试输入信号应易 于通过实验仪器产生。 3.2.1 常用测试输入信号 常用测试信号： 单位阶跃函数和单位脉冲函数 在初始时刻的速度均为无穷大 函数，前者的新稳态为1，而 后者无新稳态。单位阶跃函数 是理想的测试信号，但其初始 时刻之后速度为零，因此不适 合用来测试系统跟随速度变化 的输入信号的能力

3.2测试输入信号与时域性能指标(e)3.2.2时域性能指标Jme±(aM.时域动态性能指标?(ea)瞬态响应瞬态响应性能指标xel稳态响应稳态响应性能指标系统的响应瞬态响应：在输入信号作用下系统从初始状态到最终状态的典型阶跃响应及动态妊能指标时间响应过程。（系统输出）稳态响应：系统输出量的稳态分量或者当时间趋于无穷大时，系统输出对阶跃响应的稳态值y(o)瞬态响应由瞬态分量和稳态分量组成，其中的稳态分量就是系统的稳态响应。瞬态响应描述了系统的过渡过程，而稳态响应反映了系统的稳态精度

3.2 测试输入信号与时域性能指标 ❖ 时域动态性能指标 ●瞬态响应性能指标 瞬态响应 ●稳态响应性能指标 稳态响应 ❖ 系统的响应 ●瞬态响应 ：在输入信号作用下， ●系统从初始状态到最终状态的 时间响应过程。（系统输出） ●稳态响应：系统输出量的稳态分量或者当时间趋于无 穷大时，系统输出对阶跃响应的稳态值y()。 ●瞬态响应由瞬态分量和稳态分量组成，其中的稳态分 量就是系统的稳态响应。瞬态响应描述了系统的过渡 过程，而稳态响应反映了系统的稳态精度。 3.2.2 时域性能指标

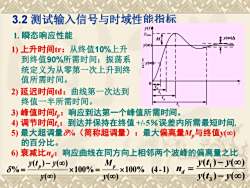
3.2测试输入信号与时域性能指标(t)tymar1.瞬态响应性能±(c0)My(o)1）上升时间tr：从终值10%上升到终值90%所需时间：振荡系y(oo)统定义为从零第一次上升到终值所需时间。曲线第一次达到2）延迟时间td：终值一半所需时间3）峰值时间t，：响应到达第一个峰值所需时间。4）调节时间t：到达并保持在终值+/-5%误差内所需最短时间5）最大超调量%（简称超调量）：最大偏离量M，与终值y（0）的百分比。响应曲线在同方向上相邻两个波峰的偏离量之比6)衰减比ng:M= y(t)- y(o0)y(t,)- y(o0)D5% =x100%x100% (4-1) ny(0)y(t3) - y(00)y(o)

3.2 测试输入信号与时域性能指标 1) 上升时间tr：从终值10%上升 到终值90%所需时间；振荡系 统定义为从零第一次上升到终 值所需时间。 2) 延迟时间td：曲线第一次达到 终值一半所需时间。 3) 峰值时间tp：响应到达第一个峰值所需时间。 4) 调节时间t s：到达并保持在终值+/-5％误差内所需最短时间. 5) 最大超调量%（简称超调量）：最大偏离量Mp与终值y() 的百分比。 6) 衰减比nd：响应曲线在同方向上相邻两个波峰的偏离量之比 100% (4 -1) ( ) 100% ( ) ( ) ( ) %    =  −  = y M y y t y p p  ( ) ( ) ( ) ( ) 3 1 −  −  = y t y y t y nd t y(t) 0 ( ) 2 1 y  y() max y  y() d t rt p t s t Mp 1. 瞬态响应性能

3.2测试输入信号与时域性能指标7）振荡次数：指响应曲线在调节时间内偏离稳态值振荡的次数：若振荡周期为TS，则振荡次数Ns=ts/Ts：2.稳态响应性能指标R(s) E(s)Y(s)+Gk(s)从输入端定义，系统误差定义为e(t)=r(t)-b(t) (3-2)B(s)H(s)稳态误差：ess = e(t) lt-0 = e(00)两种定义之间尽管数值可以不从输出端定义：若同，但经过传感器或测量装置系统误差=输出期望值一实际值量纲换算后是完全等价的。e(t)= y。(t)-y(t) (3-3)稳态误差：e=é(t)lt-=é()本书采用第一种定义方法

3.2 测试输入信号与时域性能指标 7) 振荡次数：指响应曲线在调节时间内偏离稳态值振荡的 次数；若振荡周期为Ts，则振荡次数Ns=ts/Ts . e(t) = r(t)-b(t) (3- 2) 从输入端定义，系统误差定义为： 2. 稳态响应性能指标 = ( )| = () → e e t e s s t 稳态误差： ( ) ~ ( )| ~ ~ ( ) ( ) ( ) (3-3) ~ s s = t =  = − = − → e e t e e t y t y t o 稳态误差： 系统误差 输出期望值 实际值， 从输出端定义：若 R(s) E(s) H(s) Y(s) G (s) k B(s) 两种定义之间尽管数值可以不 同，但经过传感器或测量装置 量纲换算后是完全等价的。 本书采用第一种定义方法

3.3一阶系统的时域分析3.3.1一阶系统的一般形式R(s)Y(s)1T dy(0)KTs+ y(t)= Kr(t) (3- 4)dtT：描述系统惯性的时间常数1Y(s)传递函数K：对输入信号进行放大的放大系数Ts +1R(s)由图（a）可见，要研究系统内部的本质，只需研究系统的单位阶跃或单位脉冲等函数的响应即可，不失一般jos平面地可考虑K=1。3.3.2一阶系统的单位阶跃响应单位阶跃响应：01T11R(s) =Y(s)(3-6)三Ts +1Ts +1s(Ts + 1)ST1= L-'[Ys(s)+Y(s)]= ys(t)-y(t) =1-e-1/T, t≥0y(t)= L(3-7)Ts +1S

3.3 一阶系统的时域分析 3.3.1 一阶系统的一般形式 对输入信号进行放大的放大系数 描述系统惯性的时间常数 : : ( ) ( ) (3 - 4) ( ) K T y t K r t dt dy t T + = 1 1 ( ) ( ) + = R s Ts Y s 传递函数： (3 - 6) 1 1 ( 1) 1 ( ) 1 1 ( ) + = − + = + = Ts T s Ts s R s Ts Y s 单位阶跃响应： [ ( ) ( )] ( ) ( ) 1 , 0 (3- 7) 1 1 ( ) 1 1 / = + = − = −        + = − − − − L Y s Y s y t y t e t Ts T s y t L t T s s t s s t 3.3.2 一阶系统的单位阶跃响应 j T 1 − s 平面 0  s 1 T R(s) K Y(s) 由图（a）可见，要研究系统内部的本质，只需研究系 统的单位阶跃或单位脉冲等函数的响应即可，不失一般 地可考虑K=1

初始斜率！J(t)43.3一阶系统的时域分析T3.3.2一阶系统的单位阶跃响应稳态分量：ss(t)=10.9820.95瞬态分量: y,(t)=-e-t/T0.8650.6321)以无因次时间=t/T取++T2T3T4T0不同值时的输出1）一阶系统单位阶跃响应的tr、t。和ty(0)=1-e,均正比于时间常数。y(T) = 1- e-1 = 0.632,t=2.20T，t=0.69T，t=3T或4T（4=0.05或0.02）y(2T) =1- e-2 = 0.865,2）时间常数越大，系统的惯性越大响应过程越长，反之，系统的惯性越小，响应过程越快。y() = 12)当=1,2,3,,8时，响应曲线斜率dy(t)1dy(t)dy(t)dy(t)1=0.368=0=0.135T'TFdtdtdtdt=0(=Tt=2Tt=00

3.3 一阶系统的时域分析 t T t y t e / ss ( ) y (t) 1 − = − = 瞬态分量： 稳态分量： ( ) 1 , (2 ) 1 0.865, ( ) 1 0.632, (0) 1 , : 1) t / T 2 1 0  = = − = = − = = − = − − y y T e y T e y e  不同值时的输出 以无因次时间 取 2)当 = 1, 2, 3,  , 时，响应曲线斜率： 0 ( ) , , 1 0.135 ( ) , 1 0.368 ( ) , ( ) 1 0 2 = = = = t= t=T t= T t= dt dy t dt T dy t dt T dy t dt T dy t  1）一阶系统单位阶跃响应的tr、td和ts 均正比于时间常数。 t r=2.20T，td=0.69T，t s=3T或4T （=0.05或0.02） 2）时间常数越大，系统的惯性越大， 响应过程越长，反之，系统的惯性越小， 响应过程越快。 3.3.2 一阶系统的单位阶跃响应 T 2T 3T 4T t 0 y(t)1 0.632 0.865T 1 初始斜率 0.95 0.982

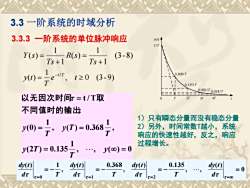
3.3一阶系统的时域分析3.3.3一阶系统的单位脉冲响应t)1/T1Y(s(3-8)RTs + 1Ts +110.368/T-t/Tt≥0(3-9)V1T0.135/TV0.050/T0.018/T3二===三华以无因次时间t=t/T取2TT3T4T0不同值时的输出1只有瞬态分量而没有稳态分量2）另外，时间常数T越小，系统y(T) = 0.368y(0) :响应的快速性越好，反之，响应过程增长。福y(2T) = 0.135y() = 0T0.368dy(t)dy(t)dy(t)0.135dy(t)= 0TTTdtdtdtdt0T=1T=2T=00

3.3 一阶系统的时域分析 3.3.3 一阶系统的单位脉冲响应 (3-8) 1 1 ( ) 1 1 ( ) + = + = Ts R s Ts Y s , 0 (3-9) 1 ( ) / =  − e t T y t t T , , ( ) 0 1 (2 ) 0.135 , 1 , ( ) 0.368 1 (0) : t / T =  = = = = y T y T T y T T y  不同值时的输出 以无因次时间 取 0 ( ) , , ( ) 0.135 , ( ) 0.368 , ( ) 1 0 1 2 = − = − = − =  =  =  =  =    d d y t d T d y t d T d y t d T d y t  1）只有瞬态分量而没有稳态分量 2）另外，时间常数T越小，系统 响应的快速性越好，反之，响应 过程增长。 0 T 2T 3T 4T t y(t) 1/T 0.135 /T 0.368 /T 0.050 /T 0.018/T