《自动控制原理》课程教学资源（电子教案）第五章 线性系统的频域分析法（1/2）

第5章线性系统的频域分析法Frequency-response analysis5.1频率特性及其表示法幅相曲线对数频率特性曲线5.2典型环节的幅相曲线5.3稳定裕度和判据已经学习了用线性常微分方程和传递函数描述线性定常系统，这两种模型分别在时域和复频域中对系统进行了描述。下面介绍一种数学模型一频率特性函数，这种模型是对系统的一种频域刻画，在系统分析中有重要作用。①判断系统是否稳定，②稳定程度一一稳定裕度。应用频率特性研究线性系统的经典方法称为频域分析法。（是以传递函数为基础的又一种图解法。与根轨迹法相比较，根轨迹法是一种非常实用的求取闭环特征方程式根的图解法，特别对于高阶系统）与其他方法相比较，频率响应法还具有如下特点：（1）频率特性具有明确的物理意义，它可以用实验的方法来确定，这对于难以列写微分方程式的元部件或系统来说，具有重要的实际意义。（2）由于频率响应法主要通过开环频率特性的图形对系统进行分析，97

97 第 5 章 线性系统的频域分析法 Frequency-response analysis 5.1 频率特性及其表示法 幅相曲线 对数频率特性曲线 5.2 典型环节的幅相曲线 5.3 稳定裕度和判据 已经学习了用线性常微分方程和传递函数描述线性定常系统，这两种 模型分别在时域和复频域中对系统进行了描述。下面介绍一种数学模型— —频率特性函数，这种模型是对系统的一种频域刻画，在系统分析中有重 要作用。判断系统是否稳定，稳定程度——稳定裕度。 应用频率特性研究线性系统的经典方法称为频域分析法。（是以传递函 数为基础的又一种图解法。与根轨迹法相比较，根轨迹法是一种非常实用 的求取闭环特征方程式根的图解法，特别对于高阶系统）。 与其他方法相比较，频率响应法还具有如下特点： （1）频率特性具有明确的物理意义，它可以用实验的方法来确定，这 对于难以列写微分方程式的元部件或系统来说，具有重要的实际意义。 （2）由于频率响应法主要通过开环频率特性的图形对系统进行分析

因而具有形象直观和计算量少的特点。（3）频率响应法不仅适用于线性定常系统，而且还适用于传递函数不是有理数的纯滞后系统和部分非线性系统的分析。5.1频率特性及其表示法5.1.1频率特性的基本概念频率特性又称频率响应，它是系统（或元件）对不同频率正弦输入信号的响应特性。设线性系统的输入为一频率为的正弦信号，在稳态时，系统的输出具有和输入同频率的正弦函数，但其振幅和相位一般均不同于输入量，且随着输入信号频率的变化而变化，如图5.1所示。线性系统图98

98 因而具有形象直观和计算量少的特点。 （3）频率响应法不仅适用于线性定常系统，而且还适用于传递函数不 是有理数的纯滞后系统和部分非线性系统的分析。 5.1 频率特性及其表示法 5.1.1 频率特性的基本概念 频率特性又称频率响应，它是系统（或元件）对不同频率正弦输入信号的 响应特性。设线性系统的输入为一频率为的正弦信号，在稳态时，系统的 输出具有和输入同频率的正弦函数，但其振幅和相位一般均不同于输入量， 且随着输入信号频率的变化而变化，如图 5.1 所示。 0 0.5 1 1.5 2 2.5 3 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 线 性 系 统 0 0.5 1 1.5 2 2.5 3 -5 -4 -3 -2 -1 0 1 2 3 4 5 图

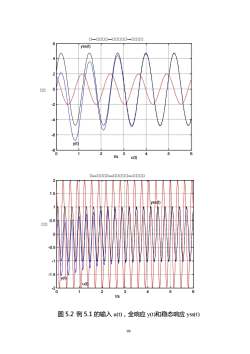
00000000000000Cyss(t)吕-2-4-6Vy(t)-82356014t/su(t)口口口0口-口口口口-1.5yss(t)0.5吕00.5-1-1.5U123456t/s图5.2例5.1的输入u(t)，全响应y(t)和稳态响应yss(t)99

99 0 1 2 3 4 5 6 -8 -6 -4 -2 0 2 4 6 t/s 幅幅 u(t) y(t) yss(t) 幅—幅幅幅幅—幅幅幅幅幅—幅幅幅幅 0 1 2 3 4 5 6 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 t/s 幅幅 u(t) y(t) yss(t) 幅—幅幅幅幅—幅幅幅幅幅—幅幅幅幅 图 5.2 例 5.1 的输入 u(t)，全响应 y(t)和稳态响应 yss(t)

10s +50考虑系统传递函数为G(s)=s2 +4s+3u(t)=2cos(5t+30°)u(t) = 2cos(20t + 300)设系统的传递函数为 C%=G(s)=U)V(s)R(s)Ao已知输入r(t)=Asin(ot），其拉氏变换R(s)=4，A 为常量，则系统输出U(s)Ao为C(s) = G(s)R(s)= V(s) s2 +02U(s)Ao(5-1)(s$+ p:)(s+ p2).(s+ pn) ? +02式中，-Pl-P2…-p,为G(s)的极点。对于稳定系统，这些极点都位于s平面的左方，即它们的实部均为负值。为简单起见，令G(s)的极点均为相异的实数极点，则式(5-1)改写为C(s)=_baa(5-2)?s+pis+jos-joa,a和b,(i=1,2,n)均为待定系数。对上式取拉氏反变换，求得c(t)= ae-jot +e jan +b,e-P)(5-3)i=1当t→时，系统响应的瞬态分量be-pt趋向于零，其稳态分量为i=lc(t)= ae-jon +aejor(5-4)其中系数由下式确定AoAo()+jo)=G()a=G(s)-+a2($+ jo)l2100

100 考虑系统传递函数为 4 3 10 50 ( ) 2 + + + = s s s G s u(t) = 2cos(5t + 30) u(t) = 2cos(20t + 30) 设系统的传递函数为 ( ) ( ) ( ) ( ) ( ) V s U s G s R s C s = = 已知输入 r(t) = Asin(t) ，其拉氏变换 2 2 ( )   + = s A R s ，A 为常量，则系统输出 为 2 2 ( ) ( ) ( ) ( ) ( )   + = = s A V s U s C s G s R s 2 2 1 2 ( )( ) ( ) ( )   +  + + + = s A s p s p s p U s  n (5-1) 式中，− p −p − pn , , 1 2 为 G(s)的极点。对于稳定系统，这些极点都位于 s 平 面的左方，即它们的实部均为负值。为简单起见，令 G(s)的极点均为相异 的实数极点，则式(5-1) 改写为  s j a s j a s p b C s n i i i − + + + + =  =1 ( ) (5-2) a,a b (i 1,2, n) 和 i =  均为待定系数。对上式取拉氏反变换，求得  = − − = + + n i p t i j t j t i c t ae ae b e 1 ( )   (5-3) 当 t →  时，系统响应的瞬态分量  = − n i p t i i b e 1 趋向于零，其稳态分量为 j t j t t c t ae ae   = + − → ( ) (5-4) 其中系数由下式确定 j A s j G j s j s j A s j G j s A a G s s j s j 2 ( ) ( ) ( )( ) ( ) ( ) ( ) 2 2 − + = − + − + = − + = =− =−            (5-5)

AoAoA(5-6)a=G(s)? +@2(s- jo)=G(jo)=G(j@)(s-jo))(s+ jo)(s- jo)(s21由于G(jo)是一个复数向量，因而可表示为Gja) = a()+ jb) = G(jo)e km= A(0)ej(o)(5-7)c(0)+ jd(0)因为G(s)的分子和分母多项式为实系数,故a(の)和c(の)为关于的偶次幂实系数多项式，b(の)和d(の)为关于の的奇次幂实系数多项式，即a(の)和c()为の的偶函数，b(の)和d(の)为の的奇函数。(jo)4 = @4(jo)"= jo(jo)?=-o?(jo)3 =-j03(5-8)In = 0,2,4,...j02n+1[n=0,2,4,...2n(jo)2n+lGjo)2n-jo2n+1[n= 1,3,5,..n= 1,3,5,..a?(0) +b (0)(5-9)JG(jo)] =Nc(0)+d?(0)b(の)d(o)(5-10)-argig/GUa) arg g (c(の)G(-j 0) = a(0) jb -I (j0)e km= A(0)e-jg(α)(5-11)c(o)- jd(o)[A(0) =|G(jo)]/ G(ja)(5-12)[(0)= /G(ja)将式(5-5)、式(5-6)、式(5-7)和式(5-11)代入式(5-4)，求得c()=e +e= A(0)e-()+A()e)=A(0)si(+()2j2j(5-13)以上证明了线性系统的稳态输出是和输入具有相同频率的正弦信号，101

101 j A s j G j s j s j A s j G j s A a G s s j s j 2 ( ) ( ) ( )( ) ( ) ( ) ( ) 2 2            − = + − − = + = = = (5-6) 由于 G( j) 是一个复数向量，因而可表示为 ( ) ( ) ( ) ( ) ( ) ( ) ( )        G j j G j e c jd a jb G j = + + = ( ) ( )    j = A e (5-7) 因为 G(s)的分子和分母多项式为实系数 ，故 a()和c() 为关于  的偶次幂实 系数多项式， b()和d() 为关于  的奇次幂实系数多项式，即 a()和c() 为  的偶函数， b()和d() 为  的奇函数。    = =    − =    = =    − = = = − = − = + + +     1,3,5, 0,2,4, ( ) 1,3,5, 0,2,4, ( ) ( ) ( ) ( ) ( ) 2 2 2 2 1 2 1 2 1 1 2 2 3 3 4 4 n n j n n j j j j j j j j j n n n n n n               (5-8) ( ) ( ) ( ) ( ) ( ) 2 2 2 2      c d a b G j + + = (5-9) ( ) ( ) arg ( ) ( ) arg ( )      c d tg a b tg G j = − (5-10) ( ) ( ) ( ) ( ) ( ) ( ) ( )        G j j G j e c jd a jb G j − = − − − = ( ) ( )    j A e − = (5-11)      = = ( ) ( ) ( ) ( )      G j A G j G( j) (5-12) 将式(5-5) 、式(5-6)、 式(5-7)和 式(5-11)代入式 (5-4)，求得 ( ) sin( ( )) 2 ( ) 2 ( ) ( ) ( ) ( )               + = + − = + = − − − A A t j A A e e j A c t ae ae A e e j t j t j j t j j t (5-13) 以上证明了线性系统的稳态输出是和输入具有相同频率的正弦信号

其输出与输入的幅值比为A()=|G(jo)，输出与输入的相位差p(の) :G(jo)下面以R-C电路为例，说明频率特性的物理意义。图5-3所示电路的传递函数为Ru.8ui0oU。(s)图5-3R-C电路2=G(s)(5-14)U,(s)1 + RCs设输入电压u,(t)=Asin(ot），由复阻抗的概念求得1U.G0) =GGj0)= I+Rja" 1+Tjo1(5-15)U,(jo)如上所述，G(j)可以改写为G(jo)=|G(jo)ej0(a)(5-16)式中, T=RC ; JG(jo)=;p(o)=-arctgToV1+T202G(j）称为电路的频率特性。显然，它由该电路的结构和参数决定，与输入信号的幅值与相位无关。|G(jo)是G(jo)的幅值，它表示在稳态时，电路的输出与输入的幅值之比。(の)是G(jの)的相角，它表示在稳态时，输出信号与输入信号的相位差。由于G(jの)和p(の)都是输入信号频率の的函数，故102

102 其输出与输入的幅值比为 A() = G( j) ，输出与输入的相位差 ( ) ( )    G j = 。 下面以 R-C 电路为例，说明频率特性的物理意义。图 5-3 所示电路的 传递函数为 R 图5-3 R-C电路 C i u uo RCs G s U s U s i o + = = 1 1 ( ) ( ) ( ) (5-14) 设输入电压 u (t) Asin( t) i =  ，由复阻抗的概念求得      RCj Tj G j U j U j i o + = + = = 1 1 1 1 ( ) ( ) ( ) (5-15) 如上所述， G( j) 可以改写为 ( ) ( ) ( )     j G j = G j e (5-16) 式中， T = RC ； 2 2 1 1 ( )   T G j + = ； () = −arctgT G( j) 称为电路的频率特性。显然，它由该电路的结构和参数决定，与输 入信号的幅值与相位无关。 G( j) 是 G( j) 的幅值，它表示在稳态时，电路 的输出与输入的幅值之比。 () 是 G( j) 的相角，它表示在稳态时，输出信 号与输入信号的相位差。由于 G( j) 和 () 都是输入信号频率  的函数，故

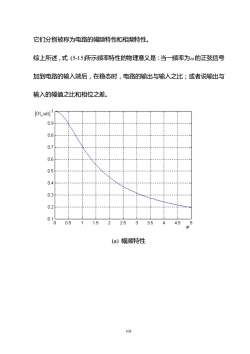
它们分别被称为电路的幅频特性和相频特性。综上所述，式（5-15)所示频率特性的物理意义是：当一频率为@的正弦信号加到电路的输入端后，在稳态时，电路的输出与输入之比；或者说输出与输入的幅值之比和相位之差G(ja)]0.90.80.70.60.50.4 0.30.2 0.100.51.52.533.524.514(a) 幅频特性103

103 它们分别被称为电路的幅频特性和相频特性。 综上所述，式 (5-15)所示频率特性的物理意义是：当一频率为  的正弦信号 加到电路的输入端后，在稳态时，电路的输出与输入之比；或者说输出与 输入的幅值之比和相位之差。 (a) 幅频特性

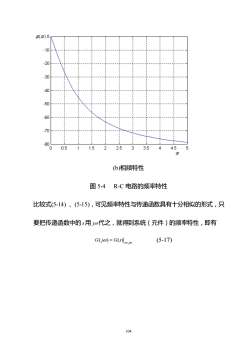
28)0-10-20-3040-50-60-70---800.51.52.533.524.5501@(b)相频特性图5-4R-C电路的频率特性比较式(5-14）、（5-15），可见频率特性与传递函数具有十分相似的形式，只要把传递函数中的s用jo代之，就得到系统（元件）的频率特性，即有G(jo) = G(s)l-=jio(5-17)104

104 (b)相频特性 图 5-4 R-C 电路的频率特性 比较式(5-14) 、(5-15)，可见频率特性与传递函数具有十分相似的形式，只 要把传递函数中的 s 用 j 代之，就得到系统（元件）的频率特性，即有   s j G j G s = ( ) = ( ) (5-17)

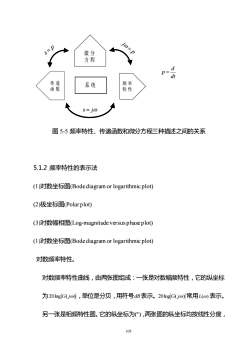
jo=p微分方程dpdt传递频率系统函数特性s=jo图5-5频率特性、传递函数和微分方程三种描述之间的关系5.1.2频率特性的表示法(1)对数坐标图(Bodediagramorlogarithmicplot）(2)极坐标图(Polarplot)(3)对数幅相图(Log-magnitudeversusphaseplot)(1)对数坐标图(Bodediagramorlogarithmicplot)对数频率特性。对数频率特性曲线，由两张图组成：一张是对数幅频特性，它的纵坐标为20log|G(jo)，单位是分贝，用符号dB表示。20logG(jo)常用L(の)表示。另一张是相频特性图。它的纵坐标为("），两张图的纵坐标均按线性分度，105

105 频 率 特 性 传 递 系 统 函 数 微 分 方 程 s = j p j =  p s = dt d p = 图 5-5 频率特性、传递函数和微分方程三种描述之间的关系 5.1.2 频率特性的表示法 (1)对数坐标图(Bode diagram or logarithmic plot) (2)极坐标图(Polar plot) (3)对数幅相图(Log-magnitude versus phase plot) (1)对数坐标图(Bode diagram or logarithmic plot) 对数频率特性。 对数频率特性曲线，由两张图组成：一张是对数幅频特性，它的纵坐标 为 20log G( j) ，单位是分贝，用符号 dB 表示。 20log G( j) 常用 L() 表示。 另一张是相频特性图。它的纵坐标为()，两张图的纵坐标均按线性分度

横坐标是角速率の，采用1g(の)分度(为了在一张图上同时能展示出频率特性的低频和高频部分）。故坐标点の不得为零。1到10的距离等于10到100的距离，这个距离表示10倍频程，用dec表示。优点：①幅频特性的乘除运算转变为加减运算。②对系统作近似分析时，只需画出对数幅频特性曲线的渐进线，大大简化了图形的绘制。③用实验方法，将测得系统（或环节）频率响应の→0～8得数据画在半对数坐标纸上。根据所作出的曲线，估计被测系统的传递函数(2)极坐标图(Polarplot），幅相频率特性曲线，幅相曲线频率特性是复数。G(jo)可用幅值G(jo)和相角β(の)的向量表示。当输入信号的频率の由变化时，向量G(jo)的幅值和相位也随之作相应的变化，其端点在复平面上移动的轨迹称为极坐标图。这种图形主要用于对闭环系统稳定性的研究，奈奎斯特(N.Nyquist)在1932年基于极坐标图阐述了反馈系统稳定性的论证。利用开环频率特性研究闭环系统的稳定性，而不必解出特征根。为纪念他对控制系统作出的贡献，这种图又名奈奎斯特曲线，简称奈氏图。5.2典型环节频率特性曲线的绘制106

106 横坐标是角速率  ，采用 lg() 分度(为了在一张图上同时能展示出频率特 性的低频和高频部分)。故坐标点  不得为零。1 到 10 的距离等于 10 到 100 的距离，这个距离表示 10 倍频程，用 dec 表示。 优点：幅频特性的乘除运算转变为加减运算。对系统作近似分析时， 只需画出对数幅频特性曲线的渐进线，大大简化了图形的绘制。用实 验方法，将测得系统（或环节）频率响应  →0 ~  得数据画在半对数坐 标纸上。根据所作出的曲线，估计被测系统的传递函数。 (2)极坐标图(Polar plot)，幅相频率特性曲线，幅相曲线 频率特性是复数。 G( j) 可用幅值 G( j) 和相角 () 的向量表示。当输入 信号的频率  由变化时，向量 G( j) 的幅值和相位也随之作相应的变 化，其端点在复平面上移动的轨迹称为极坐标图。这种图形主要用于对 闭环系统稳定性的研究，奈奎斯特(N.Nyquist)在 1932 年基于极坐标图阐 述了反馈系统稳定性的论证。利用开环频率特性研究闭环系统的稳定 性，而不必解出特征根。为纪念他对控制系统作出的贡献，这种图又名 奈奎斯特曲线，简称奈氏图。 5.2 典型环节频率特性曲线的绘制