《测量学》课程教学资源（章节习题，23988）第七章 控制测量（答案）

7.2试题解答 7.2.1名词解释题 ()控制点组成三角形，通过测量各三角形的内角，已知一个点的坐标，根据不同的图形 有的要测量一条边长（基线）及方位角，然后通过计算求得各控制点的坐标。 (2)直接为测绘地形图而布设的控制点，作为测图的根据点。 (3)为测绘地形图而布设控制点进行的控制测量，一般有图根三角测量及图根导线测量 两种。 (4)国家基本控制网的各类控制点，包括三角点、导线点、水准点及GS点。 (⑤)将测区内相邻控制点连成直线而构成的折线。 (6)在测区布设控制点成闭合多边形或折线形，测量导线边长及导线边所夹的水平角。 (7)闭合导线所有坐标增量总和，理论上应为零，如不为零，其值即为坐标增量闭合差 附合导线坐标增量闭合差是指坐标增量总和与己知两高级点之间坐标差的较差。 (8)在测站上通过观测目标的竖角，丈量仪器高及目标高，己知测站与目标间 水平距，按三角学的原理，便可求得测站与目标的高差。 (9)测量得高差总和不等于理论值或不等于所附合的两己知点的高程之差。 (10)地球曲率差和大气折光差对高差进行的改正。 7.2.2填空题 (1)平面高程 三角测量、三边测量、边角测量、导线测量水准测量三角 高程测量 (2)四标石觇标 (3)图根 小三角测量、测角交会、测边交会、导线测量 (4)一条基线基线的方位角各边长、各边方位角各点的坐标 (⑤)控制测区范围小，边长短，测角精度要求高近似平差计算 (6)不超过测图的最大视距的1.7倍±20”1：10000±60” (7)4个4个 (8)首级控制图根控制 (9)测图比例尺地物地貌的复杂程度 (10)闭合导线附合导线支导线 (11)平均分配角度闭合差，而符号相反。如不能平均分配，则可对短边夹角和长、短边 夹角给以较大的改正数。 (12)角度边长测边测角 (13)经纬仪导线测量视距导线测量视差导线测量电磁波测距导线测量 (14踏查选点埋桩测量导线右角（左角）测量导线边长测量起始边方位角或 与己知高级边的连结，测量连结角与连接边 (15)导线点的坐标导线点的高程角度闭合差的计算与调整方位角的推算计 算各边的坐标增量坐标增量闭合差的计算与调整推算各导线点坐标 (16)两点的边长和方位角纵坐标增量、横坐标增量 两点的纵坐标增量、横坐标增量两点的边长和方位角 (17)四四五等水准测量三角高程测量 (18)S3红黑双面红黑面水准尺黑面测量和红面 (19)三角学三角测量竖直角仪器高和目标的靓标高 (20)三、四等水准测量三角高程测量 7.2.3是非判断题

7.2 试题解答 7.2.1 名词解释题 (1)控制点组成三角形，通过测量各三角形的内角，已知一个点的坐标，根据不同的图形 有的要测量一条边长(基线)及方位角，然后通过计算求得各控制点的坐标。 (2)直接为测绘地形图而布设的控制点，作为测图的根据点。 (3)为测绘地形图而布设控制点进行的控制测量，一般有图根三角测量及图根导线测量 两种。 (4)国家基本控制网的各类控制点，包括三角点、导线点、水准点及 GPS 点。 (5)将测区内相邻控制点连成直线而构成的折线。 (6)在测区布设控制点成闭合多边形或折线形，测量导线边长及导线边所夹的水平角。 (7)闭合导线所有坐标增量总和，理论上应为零，如不为零，其值即为坐标增量闭合差。 附合导线坐标增量闭合差是指坐标增量总和与已知两高级点之间坐标差的较差。 (8)在测站上通过观测目标的竖角，丈量仪器高及目标高，已知测站与目标间 水平距，按三角学的原理，便可求得测站与目标的高差。 (9)测量得高差总和不等于理论值或不等于所附合的两已知点的高程之差。 (10)地球曲率差和大气折光差对高差进行的改正。 7.2.2 填空题 (1)平面 高程 三角测量、三边测量、边角测量、导线测量 水准测量 三角 高程测量 (2)四 标石 觇标 (3)图根 小三角测量、测角交会、测边交会、导线测量 (4)一条基线 基线的方位角 各边长、各边方位角 各点的坐标 (5)控制测区范围小，边长短，测角精度要求高 近似平差计算 (6)不超过测图的最大视距的 1.7 倍 ±20″ 1:10000 ±60″ (7)4 个 4 个 (8)首级控制 图根控制 (9)测图比例尺 地物地貌的复杂程度 (10)闭合导线 附合导线 支导线 (11)平均分配角度闭合差，而符号相反。如不能平均分配，则可对短边夹角和长、短边 夹角给以较大的改正数。 (12)角度 边长 测边 测角 (13)经纬仪导线测量 视距导线测量 视差导线测量 电磁波测距导线测量 (14)踏查选点埋桩 测量导线右角（左角） 测量导线边长 测量起始边方位角或 与已知高级边的连结，测量连结角与连接边 (15)导线点的坐标 导线点的高程 角度闭合差的计算与调整 方位角的推算 计 算各边的坐标增量 坐标增量闭合差的计算与调整 推算各导线点坐标 (16)两点的边长和方位角 纵坐标增量、横坐标增量 两点的纵坐标增量、横坐标增量 两点的边长和方位角 (17)四 四 五等水准测量 三角高程测量 (18)S3 红黑双面 红黑面水准尺 黑面测量和红面 (19)三角学 三角测量 竖直角 仪器高和目标的觇标高 (20)三、四等水准测量 三角高程测量 7.2.3 是非判断题

(1)×(2)√(3)×(4)×(5)×(6)√(7)×(8)√ 7.2.4单项选择题 2a )(3)b)(4)(a(⑤(d ( ①由高级到低级，逐级加密。控制网依次为二、三、四等三角网，一、二级小三角和 ·、二、三级导线。 ②要有足够的精度， 满足最大比例尺1：500测图精度要求 ③控制网点的密度大，边长短 使用方便 ④测角精度高，一 二级小三角和图根分别为士5”、士10“和±20”：一、二、三级导 线分别为±5”、±8”、±12”。 ⑤为了便于工程放样直接使用控制点的数据，要求控制点间按坐标反算长度和实地测 量长度之比接近于1，规定投影长度变形不得大于2.5c ⑥控制层次要 规定制 三级导线， (2)典型图形有中心形，三角锁（自由锁及两边有基线的三角锁），线形锁等。中心形外 业应观测三角形的内角，丈量其中一条边的边长及测量该边的方位角。自由三角锁 仅丈量一条基线，并测定方位角，观测三角形的内角。两边有基线的三角锁，两端 必须士量两条基线，并测定它们的方位角及二角形的内角。线形锁两瑞是附合到启 级点上，不必丈量基线，条件不许，则可仅观测三角形内角：条件许可，则可测量 1~2个连接角。上述几种典型图形见图7-3： 8 自 有两条华性的三角液 图7-3 (③)中点多边形比较适合方形或圆形，且较开阔、通视条件较好的地区。该图形近似平 差应满足的几何条件有：①三角形内角和等于180°的条件：②圆周角条件，中点测 站各角和应为360°：③边长条件，从己知边按正弦定理推算回到己知边，其边长应 等于已知边。近似平差的第一步使三角形内角和满足180°，同时考虑圆周角条件， 对内角进行第一次改正 第二步考虑边长条件，对A、B角进行第二次改正 第三 步推算边长。第四步计算坐标

(1)× (2)√ (3)× (4)× (5)× (6)√ (7)× (8)√ 7.2.4 单项选择题 (1)(a) (2)(a) (3)(b) (4)(a) (5) (d) 7.2.5 问答题 (1) ①由高级到低级，逐级加密。控制网依次为二、三、四等三角网，一、二级小三角和 一、二、三级导线。 ②要有足够的精度，满足最大比例尺 1:500 测图精度要求。 ③控制网点的密度大，边长短，使用方便； ④测角精度高，一、二级小三角和图根分别为±5"、±10"和±20"；一、二、三级导 线分别为±5"、±8"、±12"。 ⑤为了便于工程放样直接使用控制点的数据，要求控制点间按坐标反算长度和实地测 量长度之比接近于 1，规定投影长度变形不得大于 2.5cm/km。 ⑥控制层次要少，规定划分一、二、三级导线，实际只用两个级别。 (2)典型图形有中心形，三角锁（自由锁及两边有基线的三角锁），线形锁等。中心形外 业应观测三角形的内角，丈量其中一条边的边长及测量该边的方位角。自由三角锁 仅丈量一条基线，并测定方位角，观测三角形的内角。两边有基线的三角锁，两端 必须丈量两条基线，并测定它们的方位角及三角形的内角。线形锁两端是附合到高 级点上，不必丈量基线，条件不许，则可仅观测三角形内角；条件许可，则可测量 1~2 个连接角。上述几种典型图形见图 7-3： 图 7-3 (3)中点多边形比较适合方形或圆形，且较开阔、通视条件较好的地区。该图形近似平 差应满足的几何条件有：①三角形内角和等于 180°的条件；②圆周角条件，中点测 站各角和应为 360°；③边长条件，从已知边按正弦定理推算回到已知边，其边长应 等于已知边。近似平差的第一步使三角形内角和满足 180°，同时考虑圆周角条件， 对内角进行第一次改正。第二步 考虑边长条件，对 A、B 角进行第二次改正。第三 步推算边长。第四步计算坐标。 不测连接角的线形锁 测一个连接角的线形锁 φ 中点多边形 自由锁 测两个连接角的线型锁 Φ1 Φ2 有两条基线的三角锁

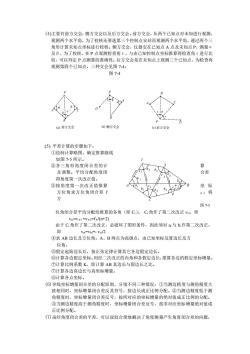
(④)主要有前方交会，侧方交会以及后方交会。前方交会，从两个已知点对未知进行观测 观测两个水平角，为了校核还要选第三个控制点安站再观测两个水平角，通过两个 角形计算未知点坐标进行校核。侧方交会，仪器安在已知点A点及未 知点P,测量 及B,为了校核，在P点观测检查角？，与由已知控制点坐标推算得检查角e进行比 较，可以判定P点测算的准确性。后方交会是在未知点上观测三个已知点，为检查再 观测第四个己知点。三种交会见图7-4： 图7-4 ()前方交会 6)侧方交会 )后方交会 (⑤)平差计算的步骤如下： ①绘制计算略图，确定推算路线 如图7.5所示。 ②各三角形角度闭合差的计 算 及调整。平均分配角度闭 合差 得角度第 一次改正值 ③按角度第一次改正值推算 坐标 方位角求方位角闭合差「 。将 图7-5 位角闭合差平均分配给推算的各角（即C)。C:角作了第二次改正V,即 V◆1曰v。2=f/（n+2) 由于C,角作了第二次改正，必破坏了图形条件，因此须对与作第二次改正， 即 V=vh=.v/位 ④求AB边长及方位角。A、B两点为高级点，由已知坐标反算边长及方 位角 ⑤假定起始边长后，按正弦定律计算其它各边假定边长 ⑥计算各边假定坐标。用经二次改正的内角和各假定边长，推算各边的假定坐标增量。 ⑦计算比例系数K,即计算AB真边长与假边长之比。 ⑦计算各边真边长与直坐标增量。 (⑥)导线坐标增量闭合差的分配原则，分别不同三种情况：①当测边精度与测角精度 致相同时，坐标增量闭合差反其符号，按边长成正比例分配。②当测边精度低于测 角精度时，坐标增量闭合差反号，按所对应的坐标增量的绝对值成正比例的分配。 ③当测边精度高于测角精度时，坐标增量闭合差反号，按非对应坐标增量绝对值成 正比倒分配 ()虽经角度闭合差的平差，可以说较合理地解决了角度测量产生角度闭合差的问题

(4)主要有前方交会，侧方交会以及后方交会。前方交会，从两个已知点对未知进行观测， 观测两个水平角，为了校核还要选第三个控制点安站再观测两个水平角，通过两个三 角形计算未知点坐标进行校核。侧方交会，仪器安在已知点 A 点及未知点 P，测量α 及β，为了校核，在 P 点观测检查角ε，与由已知控制点坐标推算得检查角ε进行比 较，可以判定 P 点测算的准确性。后方交会是在未知点上观测三个已知点，为检查再 观测第四个已知点。三种交会见图 7-4： 图 7-4 (5) 平差计算的步骤如下： ①绘制计算略图，确定推算路线 如图 7-5 所示。 ②各三角形角度闭合差的计 算 及调整。平均分配角度闭 合差 得角度第一次改正值。 ③按角度第一次改正值推算 坐 标 方位角求方位角闭合差 f β 。将 方 图 7-5 位角闭合差平均分配给推算的各角（即 Ci）。 Ci 角作了第二次改正 vci，即 vci=vφ1 =vφ2=fβ/(n+2) 由于 Ci 角作了第二次改正，必破坏了图形条件，因此须对 ai 与 bi 作第二次改正， 即 vai=vbi=- vci/2 ④求 AB 边长及方位角。A、B 两点为高级点，由已知坐标反算边长及方 位角。 ⑤假定起始边长后，按正弦定律计算其它各边假定边长。 ⑥计算各边假定坐标。用经二次改正的内角和各假定边长，推算各边的假定坐标增量。 ⑦计算比例系数 K，即计算 AB 真边长与假边长之比。 ⑦计算各边真边长与真坐标增量。 ⑧计算各点坐标。 (6)导线坐标增量闭合差的分配原则，分别不同三种情况：①当测边精度与测角精度大 致相同时，坐标增量闭合差反其符号，按边长成正比例分配。②当测边精度低于测 角精度时，坐标增量闭合差反号，按所对应的坐标增量的绝对值成正比例的分配。 ③当测边精度高于测角精度时，坐标增量闭合差反号，按非对应坐标增量绝对值成 正比例分配。 (7)虽经角度闭合差的平差，可以说较合理地解决了角度测量产生角度闭合差的问题， α’ D A C (a) 前方交会 B β β' P α (b)侧方交会 B P ε α β A A (c)后方交会 β P α ε D B C 1 Φ A a 4 3 b1 a b 2 3 4 2 2 1 c 1 c 2 3 c a 1 b 3 b c Φ 2 4 4 a B

但并非百分之百符合实际。另外，导线边长测量也存在误差。因此，虽经角度平差， 但导线仍会出现坐标增量闭合差。 (8) △X12X2X 各边高差： △X33=X3-X3 h12=H2-HI △X34=X4-X h2:=H;-H 上列各式总和得△X=0 上列各式总和得 Ch=0 同理可证 △Y=0 (9) 三角测量 导线测量 ①量距少，测角多 量距多，测角少 ②需造标，成本高 不需造标，成本较低 ③适用于山区、开阔地区等通视民 适用于建筑区、隐蔽区、森林区 好的地区 (10)相同点是：①计算步骤相同：②角度闭合差分配原则相同：③坐标增量闭合差的分 配原则相同。 不同点是：①角度闭合差计算方法不同，附合导线是由第 一条已知边方位角，经导线 转折角推算得另 一条已知边方位角，产生的不符值就是角度闭合差。闭 合导线角度闭合差是内角和不等于理论值。 ②坐标增量闭合差计算也不相同： 闭合导线是： fx=∑△x.fv=E△v 附合导线是： x=△x-(axa,=△y-ygy (11)外业工作 ①踏勘选点及建立标志选点时要求相邻点间通视良好，视野开阔，点位处土质结实 便于安置仪器，导线边长大致相等，点位分布均匀，能控制整个测区。 ②测角图根导线一般用D6级光学经纬仪，采用测回法测1测回。 ③量距图根导线般用飘尺往返丈量，往返丈量较差的相对误差不大于1/3000」 ④连测或测起始边的磁方位角如附近有高级点， 应与 高级点连接， 测连接角和连 边。如附近无高级点，则应用罗盘仪测导线起始边的磁方位角。 内业计算的目的是计算各导线点的坐标。 (12)后方交会法，至少需三个己知点，为了检查还要选第四个已知点。待定点位置最好 在三个己知点连成的三角形的重心附近。待定点观测已知点的夹角应不小于30 不大千120。 待定点若位于三个已知点组成的圆周上，则无解：若待定点在此园 附近，则求得待定点坐标精度很低，此圆称危险圆。待定点离危险圆的距离不得小 危险圆的半径的1/5。通过观测第四个已知点可求得检查角与按坐标反算方向求得检 查进行校核。如果附近没有第四个已知点，可以采用下法解决检核问题：①在任一已 知点上安置测站观测待定点与其它已知点的夹角进行检查：②可用两个待定点相互观 进行拾杏 (13)三角高程测量采用对向观测可以消除两差的影响 由1站观测2点： h12=Dtg a +i-v+f 由2站观测1点： h=Dtg a+i-v+f 往返取平均得：h(h2-he)/2=Dtga-ga)/2(i-)/2+(v)/2 从上面公式看出两差白动消除了

但并非百分之百符合实际。另外，导线边长测量也存在误差。因此，虽经角度平差， 但导线仍会出现坐标增量闭合差。 (8) ΔX12=x2-x1 各边高差： ΔX23=x3-x2 h12=H2-H1 ΔX34=x4-x3 h23=H3-H2 . . 上列各式总和得 ∑ΔX=0; 上列各式总和得 ∑h=0 同理可证 ∑ΔY=0 (9) 三 角 测 量 导 线 测 量 ①量距少，测角多 量距多，测角少 ②需造标，成本高 不需造标，成本较低 ③适用于山区、开阔地区等通视良 好的地区 适用于建筑区、隐蔽区、森林区 (10)相同点是：①计算步骤相同；②角度闭合差分配原则相同；③坐标增量闭合差的分 配原则相同。 不同点是：①角度闭合差计算方法不同，附合导线是由第一条已知边方位角，经导线 转折角推算得另一条已知边方位角，产生的不符值就是角度闭合差。闭 合导线角度闭合差是内角和不等于理论值。 ②坐标增量闭合差计算也不相同： 闭合导线是： fx=∑△x, fy=∑△y。 附合导线是： fx=∑△x-(xB-xA), fy=∑△y-(yB-yA)。 (11) 外业工作： ①踏勘选点及建立标志 选点时要求相邻点间通视良好，视野开阔，点位处土质结实 便于安置仪器，导线边长大致相等，点位分布均匀，能控制整个测区。 ②测角 图根导线一般用 DJ6 级光学经纬仪，采用测回法测 1 测回。 ③量距 图根导线一般用钢尺往返丈量 ，往返丈量较差的相对误差不大于 1/3000.。 ④连测或测起始边的磁方位角 如附近有高级点，应与高级点连接，测连接角和连接 边。如附近无高级点，则应用罗盘仪测导线起始边的磁方位角。 内业计算的目的是计算各导线点的坐标。 (12)后方交会法，至少需三个已知点，为了检查还要选第四个已知点。待定点位置最好 在三个已知点连成的三角形的重心附近。待定点观测已知点的夹角应不小于 30°， 不大于 120°。 待定点若位于三个已知点组成的圆周上，则无解；若待定点在此圆 附近，则求得待定点坐标精度很低，此圆称危险圆。待定点离危险圆的距离不得小于 危险圆的半径的 1/5。通过观测第四个已知点可求得检查角与按坐标反算方向求得检 查进行校核。如果附近没有第四个已知点，可以采用下法解决检核问题：①在任一已 知点上安置测站观测待定点与其它已知点的夹角进行检查；②可用两个待定点相互观 测进行检查。 (13)三角高程测量采用对向观测可以消除两差的影响。 由 1 站观测 2 点： h12=Dtgα1+i1-v2+f 由 2 站观测 1 点： h21=Dtgα2+ i2-v 1+f 往返取平均得： h=( h12 -h21)／2=D(tgα1-tgα2)／2+( i1- i2)／2+( v 1- v2)／2 从上面公式看出两差 f 自动消除了

(14)四等水准测量必须用双面水准尺，五等水准可以不用双面水准尺。四等水准精度要 求高，红黑面高差之差不得超过士5mm。 五等采用两次仪器高法，高差之差允许到 8mm. 四等水准要求仪器到水准尺视线长应 于100m,前后视距差应小于5m,累 计差小于10m。五等水准前后视距大致相等即可 (15)四等水准在测站上应观测前后尺的黑面中丝以及红面中丝读数，此外还应读后视上 下丝及前丝上下的读数，以便求得后尺距及前尺距。在每个测站上都应检查同一标 尺黑红面的读数差，是否为常数K(即4687或4787)，允许误差±3mm。还应检查 黑面读数 求筏 差与 红面读数求得高差之差不得超过 可搬站 由于两根 面刻划起点不同，相差为0.1m,所以当4687的标尺为后视时 红面求得高差要加 0.1m,当4787的标尺为后视，则应减0.1m,然后再和黑面高差取平均。 (16)三角高程测量适用于山区以及不便于进行水准测量的地区，并且对高程的精度要求 不高的情况下采用。它的优点：话用于地形起伏的地区，观利量少，效率高，能测 定较远目标的高程。缺点是精度不很高，距离需用其他较为精确方法测定。 (17)）解：hAB-SABtg a A+iAVB+fA hBA=SBAtg a B+iB-VA+fB h han-has 气(Sga4-Sa4gaB+i4-ig+y4-vn+f4-f)） 上式微分，并考虑SAB-SBA=S,diA=diB-OdvA=dvB-O。求得 dh dSscca,dadSsea df 0 由于|aA|≈|aB|，于是gaA≈-gaB=ga，ScaA≈saB=scd h=2gab+Sc2a-d)+d，-dl 上式转为中误差，并可以认为：mSA-mSBA=ms,maA=maB-ma,mf-mfem时 双向观测： mi mS'see'am 2 单向观测： m=gam+S2seca(g》+m 比较上面两式可得结论 ①双向观测比单向发测，边长观测与竖角观测误差的影南均减小万倍 ②为了提高三角高程测量的精度，应尽量选短边。地形控制中，交会点边长可能较大， 如再遇上α又较大，这时边长误差影响就大，因此传递高程应选竖角较小的边。 ③为减少折光差的影响，观测时间宜选中午前后3小时。 7.2.6计算题

(14)四等水准测量必须用双面水准尺，五等水准可以不用双面水准尺。四等水准精度要 求高，红黑面高差之差不得超过±5mm。五等采用两次仪器高法，高差之差允许到 8mm。四等水准要求仪器到水准尺视线长应小于 100m，前后视距差应小于 5m，累 计差小于 10m。五等水准前后视距大致相等即可。 (15)四等水准在测站上应观测前后尺的黑面中丝以及红面中丝读数，此外还应读后视上 下丝及前丝上下的读数，以便求得后尺距及前尺距。在每个测站上都应检查同一标 尺黑红面的读数差，是否为常数 K（即 4687 或 4787），允许误差±3mm。还应检查 黑面读数求得高差与红面读数求得高差之差不得超过±5mm 才可搬站。由于两根红 面刻划起点不同，相差为 0.1m，所以当 4687 的标尺为后视时，红面求得高差要加 0.1m，当 4787 的标尺为后视，则应减 0.1m，然后再和黑面高差取平均。 (16)三角高程测量适用于山区以及不便于进行水准测量的地区，并且对高程的精度要求 不高的情况下采用。它的优点：适用于地形起伏的地区，观测量少，效率高，能测 定较远目标的高程。缺点是精度不很高，距离需用其他较为精确方法测定。 (17) 解： hAB=SABtgαA+iA-vB+fA hBA=SBAtgαB+iB-vA+fB h= ( ) 2 1 2 AB A BA B A B A B A B AB BA S tg S tg i i v v f f h h = − + − + − + − −   上式微分，并考虑 SAB=SBA=S，diA=diB =0 dvA=dvB=0。求得 ( sec sec ) 2 1 " 2 2 A B B B BA B A A AB A df df d t g ds S d dh = t g ds + S − − + − ρ “ ρ       由于│αA│≈│-αB │，于是 tgαA≈-tgαB=tgα， secαA≈secαB=secα ∴ [2 · sec ( ] 2 1 2 A B A B df df d d dh = tg ds + S − ）+ − ρ “ ρ “     上式转为中误差，并可以认为：mSAB= mSBA= mS ， mαA=mαB=mα, mfA= mfB= mf ∴ 双向观测： 2 ) " .( 2 sec . 2 2 2 2 4 2 2 2 f h s S m m m tg m = + + ρ    单向观测： 2 2 2 2 4 2 2 ) " . sec .( h s mf m m = tg m + S + ρ    比较上面两式可得结论: ①双向观测比单向观测，边长观测与竖角观测误差的影响均减小 2 1 倍。 ②为了提高三角高程测量的精度，应尽量选短边。地形控制中，交会点边长可能较大， 如再遇上α又较大，这时边长误差影响就大，因此传递高程应选竖角较小的边。 ③为减少折光差的影响，观测时间宜选中午前后 3 小时。 7.2.6 计算题

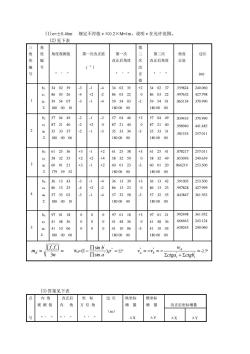
(1)e=士0.46m规定不符值e≤0.2×M仁1m,说明e在允许范围。 (2)见下表 角 角形 度 角度观测值 第一次改正值 第一次 第二次 边长 编 改正后角度 改正后角度 正弦 编号 号 ) 。， 正值 (m） 340239 A 340235 +2 340237 559824 240.060 0322 22 997632 427.798 9 5403 54 865154 370.9 1800010 1800000 1800000 570449 -3 570446 +3 570449 839433 370.990 87214 0 2 40 99894 441.485 7 -1 3 5 04 581535 257.01 1800006 1800000 1800000 b 612536 3 +2 6125 38 *3 6125 41 878217 257.011 8 58 32 59 49 853093 249.65g 6001 +3 X) 6001 23 -3 600120 866219 253.500 1795952 1800000 1800000 361343 3 361339 +3 361342 s9100s 253s00 86132 8613 997828 427.999 3302 3 573258 573255 .84384 361.952 1800010 1800000 1800000 9701 18 0 0 0 9701 18 +3 21 992498 361952 4148 36 36 666663 243.124 5 411006 0 0 411006 -3 411003 65826 240.06 1800000 1800000 1800000 v。=-vi= w =-2.7 V 3n sin a Eciga,+Ectgb (3)答案见下表 内角 改正后 坐标 边长 纵坐标 横坐标 观测值 内角 方位角 增量 增量 改正后华标增量 (m) △X △Y

(1)e=±0.46m 规定不符值ｅ≤0.2×M=1m，说明ｅ在允许范围。 (2)见下表 三 角 形 编 号 角 度 编 号 角度观测值 ° ′ ″ 第一次改正值 ( ″) 第一次 改正后角度 ° ′ ″ 第 二 次 改 正 值 第二次 改正后角度 ° ′ ″ 角度 正弦 边长 (m) 1 b1 c1 a1 Σ 34 02 39 86 03 26 59 54 07 180 00 10 -3 -4 -3 -1 +2 -1 -4 -2 -4 34 02 35 86 03 22 59 54 03 180 00 00 +2 0 -2 34 02 37 86 03 22 59 54 01 180 00 00 .559824 .997632 .865154 240.060 427.798 370.990 2 b2 c2 a2 Σ 57 04 49 87 21 40 35 33 37 180 00 06 -2 -2 -2 -1 +2 -1 -3 0 -3 57 04 46 87 21 40 35 33 34 180 00 00 +3 0 -3 57 04 49 87 21 40 35 33 31 180 00 00 .839433 .998940 .581535 370.990 441.485 257.011 3 b3 c3 a3 Σ 61 25 36 58 32 55 60 01 21 179 59 52 +3 +2 +3 -1 +2 -1 +2 +4 +2 61 25 38 58 32 59 60 01 23 180 00 00 +3 0 -3 61 25 41 58 32 49 60 01 20 180 00 00 .878217 .853093. 866219 257.011 249.659 253.500 4 b4 c4 a4 Σ 36 13 43 86 13 25 57 33 02 180 00 10 -3 -4 -3 -1 +2 -1 -4 -2 -4 36 13 39 86 13 23 57 32 58 180 00 00 +3 0 -3 36 13 42 86 13 23 57 32 55 180 00 00 .591005 .997828 .843847 253.500 427.999 361.952 5 b5 c5 a5 Σ 97 01 18 41 48 36 41 10 06 180 00 00 0 0 0 0 0 0 0 0 0 97 01 18 41 48 36 41 10 06 180 00 00 +3 0 -3 97 01 21 41 48 36 41 10 03 180 00 00 .992498 .666663 .658263 361.952 243.124 240.060 = = n f f m i i 3 [ ]  Wd= =   − " ' ' ) sin sin (1  a b 22" =  +  = − = − ' ' " " i i d a b ctga ctgb w v v -2.7" (3)答案见下表 点 号 内 角 观 测 值 °′ ″ 改正后 内 角 °′ ″ 坐 标 方 位 角 °′ ″ 边 长 （m） 纵坐标 增 量 ΔX 横坐标 增 量 ΔY 改正后坐标增量 ΔX ΔY

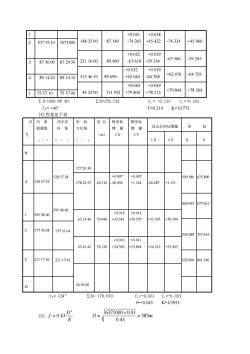
1 +0.031 2 10719101071900 1483500 87.140 -74.365 74.334 +45.460 +0.032 +0.039 873000 872950 2211600 9960 67.618 -59.334 67.586 59.295 +0.032 +0.039 3134610 89.690 +62.044 -64.768 62.076 64.729 891420 891410 +0.040 +0.049 755710755700 443200 111.952 +79.804 +78.515 +79.844 +78.564 ∑B-3600040 ∑D=378.742 ￡，=-0.135 f,=-0.165 f.=+40" f=0.214 K=1/1773 (4)答案见下表 点内角改正后 坐 标 边长 飘坐标 横坐标 观测值 内角 方位角 增量 增量 改正后坐标增量 桥 号 (m) AX AY AY 1272030 1285738 +0.007 +0.007 09.580675.890 1285732 1782252 40.51040.494 +1.144 40.487 +1.151 9.093 677.041 95080d 95080 +0.014+0.014 63144679.040+35.581 +70.579 +35.595 +70.594 1773058 1773104 04.688747.635 +0.010+0.011 654342 59120 +24.302+53.894 +24.312 +53.905 2111736 211742 29.000 342600 f=+24” D178.670 f.s-0.037 f,-0.03 f=+0.045 K=1/3953 (⑤)f=0.43D D= 6371000x0.01=385m V0.43

1 148 35 00 87.140 +0.031 -74.365 +0.038 +45.422 -74.334 +45.460 2 107 19 10 1071900 221 16 00 89.960 +0.032 -67.618 +0.039 -59.334 -67.586 -59.295 3 87 30 00 87 29 50 313 46 10 89.690 +0.032 +62.044 +0.039 -64.768 +62.076 -64.729 4 89 14 20 89 14 10 44 32 00 111.952 +0.040 +79.804 +0.049 +78.515 +79.844 +78.564 1 75 57 10 75 57 00 ∑β=360 00 40 ∑D=378.742 fx = -0.135 fy =-0.165 fβ= +40" f =0.214 K=1/1773 (4)答案见下表 点 号 内 角 观测值 °′″ 改正后 内 角 ° ′ ″ 坐 标 方位角 ° ′ ″ 边 长 （m） 纵坐标 增 量 ΔX 横坐标 增 量 ΔY 改正后坐标增量 坐 标 ΔX ΔY X Y B 127 20 30 A 128 57 32 128 57 38 509.580 675.890 178 22 52 40.510 +0.007 - 40.494 +0.007 +1.144 -40.487 +1.151 1 295 08 00 295 08 06 469.093 677.041 63 14 46 79.040 +0.014 +35.581 +0.014 +70.579 +35.595 +70.594 504.688 747.635 2 177 30 58 177 31 04 65 43 42 59.120 +0.010 +24.302 +0.011 +53.894 +24.312 +53.905 C 211 17 36 221 17 42 529.000 801.540 34 26 00 D fβ= +24″ ∑D= 178.670 fx =-0.031 fy =-0.033 f=+0.045 K=1/3953 (5) R D f 2 = 0.43 D 385m 0.43 6371000 0.01 =  =

(6)Hg-HA+ABtga+i-v=358.26+620.12Xtg2°38'+1.62-3.65 =358.26+28.52+1.62-3.65=384.75m (7)四等水准表计算如下 后下丝 下丝 方向标尺读数 平均 备 尺L 上丝 红 K+ 后距 前 距 视距差d Ed 高差 (1) (4) 后 (3) (8) (14) K为标 (2) (5) 前 (6) (7) (13) 尺常数 (9) (10の 后前 (15) (16) (17) 18) .787 (11) (12) k4- 1571 0.739 后3 1384 6.171 4.687 1.197 0.363 前4 0.551 5.239 -1 374 37.6 后-前0.833 0.932 +1 .832 -0.2 -0.2 2.121 2196 后41934 6621 0 1.747 1.821 前32.008 6.796 -1 37.4 37.5 后-前-0.074-0.175 +1 0.0745 -0.1 -0.3 7.2.7附加题 (1) (a闭合导线：s×cosa=0.∑SXsina=0 回)附合导线：ES× sa-XB-XA.ESxsina-YB-Y S和a的 分别为△S和△d 所以导线纵横坐标增量误差Mk,My为 Mx2=cos a X△S)2+(Ssin a X△a) =(Scosa x△S/S)2+Ssin a x△a)2 Mw2=(Ssin a△S/S)2+(Scos a△a)2 (1) ①当测边精度与测角精度大致相等时，即△a≈△SSk,则(I)式变为 a +sin a )k2=S2Xk2 My2=S2(sin?a +cos a )k?=2xk Mx=SXk MvESXk (2) (2)式说明纵坐标误差与距离成正比，因此坐标增量闭合差、5y应按导线边长成正 比例分配。 ②当测边精度低于测角精度时 (1)式第二项略去得 M=(Scosa△S/S)=△xXk Mv=(Ssin a△S/S)=△vXk (3 (③)式可知：纵横坐标误差与△x、△y成正比，因此坐标增量是闭合差、应 按对应边的△x及△y的绝对值大小成比例分配 ③当测边精度高于测角精度时，(1)式的第一项路去得：

(6)HB=HA+ABtgα+i-v=358.26+620.12×tg2°38′+1.62-3.65 =358.26+28.52+1.62-3.65=384.75m (7)四等水准表计算如下： 测 站 编 号 后 尺 下丝 前 尺 下丝 方 向 及 尺 号 标 尺 读 数 K + 黑-红 平 均 高 差 (m) 备 注 上丝 上丝 黑 面 红 面 后 距 前 距 视距差 d ∑d (1) (4) 后 (3) (8) (14) K 为标 尺常数 k3= 4.787 k4= 4.687 (2) (5) 前 (6) (7) (13) (9) (10) 后-前 (15) (16) (17) (18) (11) (12) 1 1.571 0.739 后 3 1.384 6.171 . 0 0.8325 1.197 0.363 前 4 0.551 5.239 -1 37.4 37.6 后-前 0.833 0.932 +1 -0.2 -0.2 2 2.121 2.196 后 4 1.934 6.621 0 - 0.0745 1.747 1.821 前 3 2.008 6.796 -1 37.4 37.5 后-前 -0.074 -0.175 +1 -0.1 -0.3 7.2.7 附加题 (1) (a) 闭合导线：∑S×cosα=0，∑S×sinα=0 (b) 附合导线：∑S×cosα=XB-XA，∑S×sinα=YB-YA 设 S 和α的误差分别为△S 和△α，所以导线纵横坐标增量误差 Mx，My 为 Mx2=(cosα×△S) 2+(Ssinα×△α) 2 =(Scosα×△S/S) 2+(Ssinα×△α) 2 My2=(Ssinα△S/S) 2+(Scosα△α) 2 （1） ①当测边精度与测角精度大致相等时，即△α≈△S/S=k，则（1）式变为 Mx2=S2 (cos2α+sin2α)k2=S2×k 2 My2=S2 (sin2α+cos2α)k2=S2×k 2 Mx=S×k My=S×k （2） (2)式说明纵坐标误差与距离成正比，因此坐标增量闭合差 fx、fy 应按导线边长成正 比例分配。 ②当测边精度低于测角精度时 (1)式第二项略去得 Mx=(Scosα△S/S)=△x×k My=(Ssinα△S/S)=△y×k （3） (3)式可知：纵横坐标误差与△x、△y 成正比，因此坐标增量是闭合差 fx、fy 应 按对应边的△x 及△y 的绝对值大小成比例分配。 ③当测边精度高于测角精度时，(1)式的第一项略去得：

x2=sin a x△a)2=△v×△a2 M2-(Scosu×△a)2=△xX△a 4 (④式中△a2为常数，所以纵横坐标误差与△y、△x成正比例，因此，坐标增 量的闭合差x、y应按非对应的△x及△y(即按△y,按△x)的绝对值大小 成比例分配。值大小成比例分配。 (2)GPS伪距定位实质上就是空间距离后方交会。此法是测定用户接收机天线至GS卫 星之间的距离P。设X、y、乙为卫星的三维坐标，X、y、z为测站的三维坐标，则 p=Vx,-x)2+0y,-2+6,- 由于卫星信号向地面传输过程中，经过电离层、对流层会产生时延，因此接收机 所测的距离并非站星间的几何距离p,称之为“伪距”，用P表示。根据推导可得： p=p+8+8.r+c8t-c8t' Vx,-x)2+0y-y)'+(e,-2c8t-p+8t8rc6t 上式即为伪距观测方程，6，为电离层延迟改正，8。为对流层延迟改正8t为 接收机钟差改正，6为卫星钟差改正， 。电离层延迟改正6可由导航电文给 出的参数求得， 对流 延政正8 根据气象资料利用公 求得 、及c6 可由导航电文中求得。因此，上式右边为可知值，只有公式左边内的4个未知数，即测 站的三维坐标x、y、z及接收机钟差改正8，所以至少需观测4颗卫星建立4个方程 式才能解算。 伪距单点定位一般采用CA码定位，定位误差达到1520m,美国施行SA技术后， CA码伪距单点定位降低到50m左右 (B)载波相位测量是测定GPS卫星载波信号到接收机天线之间的相位延迟。GS卫星载波 上调制了测距码和导航电文，所以GPS接收机接收卫星信号后，要将调制在载波上的测 距码和卫星电文去掉，重新获得纯净的载波，即所谓重建载波。GS接收机将重建载波 与接收机内由根荡器产生的本根信号通相位计比相可以得到相位差。设任意时刻t 在卫星S处的相位中，而此时经距离传播到接收机K的信号， 其相位中K,因此卫星 S至接收机K的距离p为 0=λ（φs-中K)=ANo+△φ） 式中为载波相位差（中s中K),为整周数部分，△中为不足一周的小数部分，λ为 载波波长。△中可以精确测定，但由于每颗卫星的载波相位观测方程中都有整周未知数 ,通常是用两台接收机进行相对定位。 由于载波波长短，测量距离可以得到很高的精度，目前载波相位测量相对定位精度 可达1cm~5mm

Mx2=(sinα×△α) 2=△y×△α2 My2=(Scosα×△α) 2=△x×△α2 （4） (4)式中△α2 为常数，所以纵横坐标误差与△y、△x 成正比例，因此，坐标增 量的闭合差 fx、fy 应按非对应的△x 及△y（即 fx 按△y，fy 按△x）的绝对值大小 成比例分配。值大小成比例分配。 (2)GPS 伪距定位实质上就是空间距离后方交会。此法是测定用户接收机天线至 GPS 卫 星之间的距离ρ。设 xs、ys、zs 为卫星的三维坐标，x、y、z 为测站的三维坐标，则 ρ 2 2 2 (x x) (y y) (z z) = s − + s − + s − 由于卫星信号向地面传输过程中，经过电离层、对流层会产生时延，因此接收机 所测的距离并非站星间的几何距离ρ，称之为“伪距”，用  ~ 表示。根据推导可得： ρ=  ~ +δρI+δρT+cδtk-cδt s 2 2 2 (x x) (y y) (z z) s − + s − + s − - cδtk =  ~ +δρI+δρT- cδt s 上式即为伪距观测方程，δρI为电离层延迟改正，δρT为对流层延迟改正, δtk 为 接收机钟差改正,δt s 为卫星钟差改正，c 为光速。电离层延迟改正δρI可由导航电文给 出的参数求得，对流层延迟改正δρT根据气象资料利用公式求得，xs、ys、zs 及 cδt s 可由导航电文中求得。因此，上式右边为可知值，只有公式左边内的 4 个未知数，即测 站的三维坐标 x、y、z 及接收机钟差改正δtk，所以至少需观测 4 颗卫星建立 4 个方程 式才能解算。 伪距单点定位一般采用 C/A 码定位，定位误差达到 15~20m，美国施行 SA 技术后, C/A 码伪距单点定位降低到 50m 左右。 (3)载波相位测量是测定 GPS 卫星载波信号到接收机天线之间的相位延迟。GPS 卫星载波 上调制了测距码和导航电文，所以 GPS 接收机接收卫星信号后，要将调制在载波上的测 距码和卫星电文去掉，重新获得纯净的载波，即所谓重建载波。GPS 接收机将重建载波 与接收机内由振荡器产生的本振信号通过相位计比相，可以得到相位差。设任意时刻 t, 在卫星 S 处的相位φS, 而此时经距离ρ传播到接收机 K 的信号，其相位φK, 因此卫星 S 至接收机 K 的距离ρ为 ρ=λ（φS-φK ）=λ(N0+△φ) 式中为载波相位差（φS-φK ），N0 为整周数部分，△φ为不足一周的小数部分，λ为 载波波长。△φ可以精确测定，但由于每颗卫星的载波相位观测方程中都有整周未知数 N0，通常是用两台接收机进行相对定位。 由于载波波长短，测量距离可以得到很高的精度，目前载波相位测量相对定位精度 可达 1cm~5mm