同济大学：《理论力学》课程教学课件（PPT讲稿）第二章 质点组力学 §2.4 动能定理与机械能守恒

第二章 质点组力学

第二章 质点组力学

§2.4动能定理与机械能守恒 导读 ·质点组动能定理 ·质点组的机械能 ·机械能守恒 ·柯尼希定理 ·质心系动能定理 碰撞（补充）

导 读 • 质点组动能定理 • 质点组的机械能 • 机械能守恒 • 柯尼希定理 • 质心系动能定理 • 碰撞(补充) §2.4 动能定理与机械能守恒

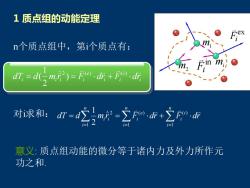
1质点组的动能定理 n个质点组中，第i个质点有： d0=d与m)=fo.d本+F0.d 对求和： n=2-a市+n 意义：质点组动能的微分等于诸内力及外力所作元 功之和

1 质点组的动能定理 i i i i e i i i i dT d m r F dr F dr       = =  +  2 ( ) ( ) ) 2 1 (    = = = = =  +  n i i i n i e i n i i i dT d m r F dr F dr 1 ( ) 1 ( ) 1 2 2 1       n个质点组中，第i个质点有： 对i求和： m1 m2 mi ex Fi  in Fi  意义: 质点组动能的微分等于诸内力及外力所作元 功之和

一 对相互作用力的功： dA=A+A,=F而+F =F.d-Fd=Fd() =F-diz 当 di2=0,dA=0 质点组的动能定理 A外+A为=E-Ek0 注意：质点组内力做功之和不等于0

一对相互作用力的功: 1 1 2 1 1 1 2 1 1 2 1 2 1 1 2 2 ( ) F dr F dr F dr F d r r dA A A F dr F dr              =  =  −  =  − = + =  +  dr12 = 0 , dA = 0  当 k k 0 质点组的动能定理 A外 + A内 = E − E 1 f  2 f  m2 m1 F1  F2  注意：质点组内力做功之和不等于0

2机械能守恒 A十A保内十A非保内=Ek一E0 A保内=%- A外+A保内=(Ek+)-(E0+VO)） A外十A保内=E-E) 如果一个系统只有保守内力作功，非保守内力 和一切外力都不做功，那么系统的总机械能保持不 变，这个系统也常称为保守系

2 机械能守恒 A A A Ek Ek 0 外 + 保内 + 非保内 = − A保内 =V0 −V ( ) ( ) A外 + A非保内 = Ek +V − Ek 0 +V0 A外 + A非保内 = E − E0 如果一个系统只有保守内力作功，非保守内力 和一切外力都不做功，那么系统的总机械能保持不 变. 这个系统也常称为保守系

注意： (1)机械能守恒定律只适用于惯性系，不适合于 非惯性系。这是因为惯性力可能做功。 (2)在某一惯性系中机械能守恒，但在另一惯性 系中机械能不一定守恒。这是因为外力的功与参 考系的选择有关。对一个参考系外力功为零，但 在另一参考系中外力功也许不为零

注意： （1）机械能守恒定律只适用于惯性系，不适合于 非惯性系。这是因为惯性力可能做功。 （2）在某一惯性系中机械能守恒，但在另一惯性 系中机械能不一定守恒。这是因为外力的功与参 考系的选择有关。对一个参考系外力功为零，但 在另一参考系中外力功也许不为零

3柯尼希定理 以物体的质心做为坐标原点，并和质心共同运动的 坐标系 已经知道 M.=∑m, ∑F=Ma. 从图知：方=元+ w蓝=”+w)

3 柯尼希定理 以物体的质心做为坐标原点，并和质心共同运动的 坐标系 c = i i Mv m v   Fi = Mac   已经知道 y x z x‘ y‘ z‘ rc ri ri ’ 从图知： ' i C i r r r    = + ( ) d d ' ( ) ( ) 2 2 i c i i e i i i F F m r t r m       = + + −

故质点组动能为 E-2m+ =m+∑mr+2m疗 考虑质心位置，则 Ek →2 柯尼希定理 意义：质点组的动能=质心的动能十相对质心动能之和

= = + n i k C i i E mr m r 1 2 ' 2 1 2 1 2     考虑质心位置，则 ——柯尼希定理 ( )    = = = = + + = + n i n i C i i C i i n i k i C i mr m r r m r E m r r 1 1 2 1 2 ' ' 2 1 2 1 ' 2 1 2             故质点组动能为 意义：质点组的动能＝质心的动能＋相对质心动能之和

4质心系动能定理 由质点相对质心的动力学方程 d里=F0+月+（←m) m: 可推出 m,2=Fd+∑ (d' 意义：质点组对质心的动能的微分，等于质点组相 对质心系位移时内力及外力所做元功之和 注意：质心虽为动点，但惯性力做功为0

4 质心系动能定理    = = =  = • + •      n i i i i n i i e i n i i i m r F r F r 1 ( ) 1 ( ) 1 2 ' d ' d ' 2 1 d     由质点相对质心的动力学方程 ( ) ( ) ( ) 2 2 i c e i i i i i F F m r dt d r m      = + + −  可推出 意义：质点组对质心的动能的微分，等于质点组相 对质心系位移时内力及外力所做元功之和. 注意：质心虽为动点，但惯性力做功为0

例1、计算第一，第二宇宙速度 (①第一宇宙速度 已知：地球半径为R,质量为M, 卫星质量为m。要使卫星在距地 面高度绕地球作匀速圆周运动， 求其发射速度。 解：设发射速度为y,绕地球的运动速度为v 机械能守恒： R-G Mm R+h 由万有引力定律和牛顿定律：G Mm (R+h) R+h

例1、计算第一，第二宇宙速度 (i) 第一宇宙速度 已知：地球半径为R，质量为M， 卫星质量为m。要使卫星在距地 面h高度绕地球作匀速圆周运动， 求其发射速度。 解： 设发射速度为v1，绕地球的运动速度为v 机械能守恒： R h Mm mv G R Mm mv G + − = − 2 2 1 2 1 2 1 由万有引力定律和牛顿定律： ( ) R h v m R h Mm G + = + 2 2 R M m