《电路理论》课程教学课件(讲稿)第8章 相量法

第8章· 相量法 本章重点 8.1 复数 8.2 正弦量 8.3 相量法的基础 8.4 电路定律的相量形式 首页
第8章 相量法 8.1 复数 8.2 正弦量 8.3 相量法的基础 8.4 电路定律的相量形式 首 页 本章重点

●重点: 1,正弦量的表示、相位差 2.正弦量的相量表示 3.电路定理的相量形式 国
2. 正弦量的相量表示 3. 电路定理的相量形式 重点: 1. 正弦量的表示、相位差 返 回

8.1复数 1.复数的表示形式 b F=a+jb 代数式 G=√-1为虚数单位) a Re F=F eio 指数式 三角函数式 F=FleF(cose+jsine)=a+jb FF1eoHF1∠0 极坐标式
1. 复数的表示形式 (j 1 为虚数单位) b F Re Im o a |F| F | F | e | F |(cos jsin ) a jb j F a jb | | | | j F F e F j F | F | e 上 页 下 页 代数式 指数式 极坐标式 三角函数式 8.1 复数 返 回

F=a+jb FF|e°=Fl∠0 IFEVa+b b 或 a=Fcose θ=arctan a 2.复数运算 ①加减运算一 采用代数式
几种表示法的关系: a b θ F a b arctan | | 2 2 或 | |sin | | cos b F a F 2. 复数运算 ①加减运算 —— 采用代数式 上 页 下 页 b F Re Im o a F a jb |F| | | | | j F F e F 返 回
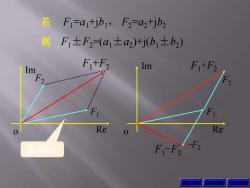
F=atjb,F2=a2+jb2 则F,±F2(a1士a2十j(b1±b2) F1+F2 m F+F2 Re Re 图解法 F-F2-F2
则 F1±F2=(a1±a2 )+j(b1±b2 ) 若 F1 =a1+jb1, F2 =a2+jb2 图解法 上 页 下 页 F1 F2 Re Im o F1+F2 -F2 F1 Re Im o F1-F2 F1+F2 F2 返 回

②乘除运算一 采用极坐标式 若F=Fl/01,F2F2/02 则:FE=FleF=FFex-) FF 20+0 模相乘 角相加 E-IFl∠0-IE1e8 Fleia-) |E|∠0,1E1e E 10-0. 模相除 角相减
②乘除运算 —— 采用极坐标式 若 F1=|F1 | 1 ,F2=|F2 | 2 1 2 2 1 j ( ) 2 1 j 2 2 j 1 2 2 1 1 2 1 | | | | | | | | | | | | 1 2 1 θ θ |F| |F| e F F F e F e F θ F θ F F θ θ θ θ 则: 1 2 1 2 j( ) 1 2 j 2 j 1 2 1 1 2 1 2 F F F F F e F e F F e 上 页 下 页 模相乘 角相加 模相除 角相减 返 回

例1 5∠47°+10∠-25°=? 解 原式=(3.41+j3.657)+(9.063-j4.226) =12.47-j0.569=12.48∠-2.61° 例2 220∠35°+07+j9)(4+j6) 20+j5 解 原式=180.2+126.2+ 19.24∠27.9°×7.211∠56.3 20.62∠14.04 =180.2+j126.2+6.728∠70.16 =180.2+j126.2+2.238+j6.329 =182.5+j132.5=225.5∠36
例 1 5 47 10 25 ? 原式 (3.41 j3.657) (9.063 j4.226) 12.47 j0.569 12.48 2.61 解 上 页 下 页 例 2 ? 20 j5 (17 j9) (4 j6) 220 35 解 原式 180.2 j126.2 20.62 14.04 19.24 27.9 7.211 56.3 180.2 j126.2 6.72870.16 180.2 j126.2 2.238 j6.329 182.5 j132.5 225.536 返 回
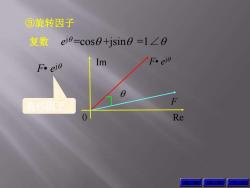
⑧旋转因子 复数ej8=cos0+jsin0=1∠0 F.eie Im 旋转因子 Re
③旋转因子 复数 e j =cos +jsin =1∠ F• e j F Re Im 0 F• e j 上 页 下 页 旋转因子 返 回

旋转因 2 cos+sm2= 0=- 。=co5+jsm-3- 0=±元,er=cos仕π)+jsin(±)=-1 乡准意+ij,1都可以看成旋转因子
j 2 π jsin 2 π cos , 2 π 2 π j e ) j 2 π ) jsin( 2 π , cos( 2 π 2 π j e π , cos( π) jsin( π) 1 j π e +j, –j, -1 都可以看成旋转因子。 特殊旋转因子 Re Im 0 F jF jF F 上 页 下 页 注意 返 回
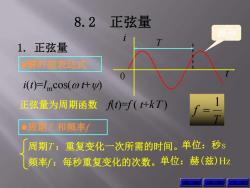
8.2 正弦量 波形 1.正弦量 ·瞬时值表达式 i(t)=Imcos(o什0 正弦量为周期函数)=f(什kT) ●周期T和频率f 周期T:重复变化一次所需的时间。单位:秒s 频率f:每秒重复变化的次数。单位:赫(兹)H五
8.2 正弦量 1. 正弦量 瞬时值表达式 i(t)=Imcos(w t+y) t i 0 T 周期T 和频率f 频率f :每秒重复变化的次数。 周期T :重复变化一次所需的时间。 单位:赫(兹)Hz 单位:秒s T f 1 正弦量为周期函数 f(t)=f ( t+kT ) 上 页 下 页 波形 返 回
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《电路理论》课程教学课件(讲稿)第6章 储能元件.pdf
- 《电路理论》课程教学课件(讲稿)第10章 含有耦合电感的电路.pdf
- 《电路理论》课程教学课件(讲稿)第11章 电路的频率响应.pdf
- 《电路理论》课程教学课件(讲稿)第16章 二端口网络.pdf
- 《电路理论》课程教学课件(讲稿)第12章 三相电路.pdf
- 《电路理论》课程教学课件(讲稿)第13章 非正弦周期电流电路和信号的频谱.pdf
- 安徽大学:《电路理论》课程教学资源(实验指导)电子技术课程设计指导.pdf
- 安徽大学:《电路理论》课程教学资源(实验指导)EDA电路仿真快速入门(Multisim).pdf
- 安徽大学:《电路理论》课程教学资源(实验指导)EDA仿真实验手册.pdf
- 安徽大学:《电路理论》课程课程学习指导(课程重点及难点、典型例题分析、样卷).pdf
- 安徽大学:《电路理论》课程授课教案(讲义,授课教师:寻丽娜).pdf
- 安徽大学:《电路理论》课程教学大纲 Electric Circuits.pdf
- 《电力系统分析》课程教学课件(讲稿)09 电力系统三相短路电流的实用计算.pdf
- 《电力系统分析》课程教学课件(讲稿)08 电力系统三相短路的暂态过程.pdf
- 《电力系统分析》课程教学课件(讲稿)06 电力系统的无功功率和电压调整.pdf
- 《电力系统分析》课程教学课件(讲稿)05 电力系统的有功功率和频率调整.pdf
- 《电力系统分析》课程教学课件(讲稿)10 电力系统各元件的序阻抗和等值电路.pdf
- 《电力系统分析》课程教学课件(讲稿)11 电力系统不对称故障的分析和计算.pdf
- 《电力系统分析》课程教学课件(讲稿)12 电力系统运行稳定性的基本概念.pdf
- 《电力系统分析》课程教学课件(讲稿)13 电力系统暂态稳定性.pdf
- 《电路理论》课程教学课件(讲稿)第9章 正弦稳态电路的分析.pdf
- 《电路理论》课程教学课件(讲稿)第3章 电组电路的一般分析.pdf
- 《电路理论》课程教学课件(讲稿)第5章 含有运算放大器的电阻电路.pdf
- 《电路理论》课程教学课件(讲稿)第4章 电路定理.pdf
- 《电路理论》课程教学课件(讲稿)第1章 电路模型和电路定律.pdf
- 《电路理论》课程教学课件(讲稿)第2章 电阻电路的等效变换.pdf
- 《机械工程控制基础》课程教学资源(讲稿)第六章 系统的性能与校正.pdf
- 《机械工程控制基础》课程教学资源(讲稿)第三章 时间响应分析.pdf
- 《机械工程控制基础》课程教学资源(讲稿)第二章 系统数学模型.pdf
- 《机械工程控制基础》课程教学资源(讲稿)第一章 绪论.pdf
- 《机械工程控制基础》课程教学资源(讲稿)第五章 系统的稳定性.pdf
- 《机械工程控制基础》课程教学资源(讲稿)第四章 频率特性分析.pdf
- 《机械工程控制基础》课程教学资源(讲稿)第六章 拉氏变换.pdf
- 中国农业大学:《工程测试技术》课程教学大纲(Measuring and Testing in Engineering).pdf
- 中国农业大学:《工程测试技术》课程授课教案(讲义)第二章 传感器.doc
- 中国农业大学:《工程测试技术》课程授课教案(讲义)第一章 测试系统及其基本特性.doc
- 中国农业大学:《工程测试技术》课程授课教案(讲义)第五章 机械工程典型参数测量技术.doc
- 中国农业大学:《工程测试技术》课程授课教案(讲义)第三章 信号的调理、记录和传输.doc
- 中国农业大学:《工程测试技术》课程教学课件(PPT讲稿)第二章 传感器.ppt
- 中国农业大学:《工程测试技术》课程教学课件(PPT讲稿)第一章 测试系统的基本特性.ppt
