中国农业大学：《工程测试技术》课程授课教案（讲义）第一章 测试系统及其基本特性

第一章测试系统及其基本特性测试系统是人们籍以了解客观事物、获取被研究对象定性、定量信息的测量仪器、实验装置以及实验方法、数据（分析）处理等方法的统称。只有正确选择测试系统并了解系统的基本特性，才能保证测量结果的准确性。通常将外界对系统的影响称为输入或激励，激励作用下系统状态的变化称为输出或响应。若将系统输出的一部分或全部反馈到输入端，则称为反馈系统或闭环系统，反之成为开环系统。若于个简单的测试系统可以组成一个复杂系统，按其组合方式可分为串联或并联系统。本章将着重讨论测量系统的特性，及其与输入、输出三者之间的关系。第一节测试系统一、测试系统的组成测试系统（图1-1）通常包括：传感器、信号调理、显示、记录以及信号分析与处理等。根据不同的测试目的，组成测试系统的功能单元可多可少，可以是单台仪器，也可以是多台仪器的组合。显示、记录被测量T传感器信号调理信号分析与处理图1-1测试系统组成传感器的主要作用是感知被测非电量（如位移、速度、加速度、压力、温度和流量等），并将其转换为电量，是测试系统的首要环节。信号调理是对传感器的输出信号进行有效变换，使之适宜传输、显示、记录和信号处理等，如，电桥、滤波、放大、调制与解调、数字化处理等。由于信号调理属于中间环节，所以也称之为中间变换。显示、记录是将测试信号以某种形式显示或记录，便于观察和分析。信号处理接受来自信号调理环节的信号，进行滤波、运算和分析等，然后以数据或图像形式输出特定信息。信号处理可使用专门的信号分析仪，也可以利用计算机信号分析软件完成。--1

一-1 第一章 测试系统及其基本特性 测试系统是人们籍以了解客观事物、获取被研究对象定性、定量信息的测量仪器、实验 装置以及实验方法、数据（分析）处理等方法的统称。只有正确选择测试系统并了解系统的 基本特性，才能保证测量结果的准确性。 通常将外界对系统的影响称为输入或激励，激励作用下系统状态的变化称为输出或响 应。若将系统输出的一部分或全部反馈到输入端，则称为反馈系统或闭环系统，反之成为开 环系统。若干个简单的测试系统可以组成一个复杂系统，按其组合方式可分为串联或并联系 统。 本章将着重讨论测量系统的特性，及其与输入、输出三者之间的关系。 第一节 测试系统 一、测试系统的组成 测试系统（图 1-1）通常包括：传感器、信号调理、显示、记录以及信号分析与处理等。 根据不同的测试目的，组成测试系统的功能单元可多可少，可以是单台仪器，也可以是多台 仪器的组合。 传感器的主要作用是感知被测非电量（如位移、速度、加速度、压力、温度和流量等）， 并将其转换为电量，是测试系统的首要环节。 信号调理是对传感器的输出信号进行有效变换，使之适宜传输、显示、记录和信号处理 等，如，电桥、滤波、放大、调制与解调、数字化处理等。由于信号调理属于中间环节，所 以也称之为中间变换。 显示、记录是将测试信号以某种形式显示或记录，便于观察和分析。 信号处理接受来自信号调理环节的信号，进行滤波、运算和分析等，然后以数据或图像 形式输出特定信息。信号处理可使用专门的信号分析仪，也可以利用计算机信号分析软件完 成。 图 1-1 测试系统组成 被测量 传感器 信号调理 显示、记录 信号分析与处理

二、线性测试系统及其基本特性如果测试系统的输出、输入具有单值对应的线性关系，则称为线性测试系统。设系统的输入为x(1)，输出为y()，则它们可用线性微分方程来表示：a.d"a.-+a 0dtdtC -b. +b.(1-1)dtdtm-1dt式中ao.al.a2a和 bo. bi,bs-b是与测量装置特性和输入状况有关的常数，它们既不随时间变化，也不是自变量x、因变量及它们各阶导数的函数。若以x(0)——y()表示线性系统的输入、输出关系，则具有以下主要性质：1、叠加特性符合叠加原理若x@n@),x2(t)-—2(t),(1-2)则[xi( ± x2(]-( ± (]2、比例特性对于任意常数，有(1-3)ax() -→ay()对输入微分的响应等于对原输入响应的微分3、微分特性d= (1- 4)d4、积分特性系统初始状态为零条件下，对输入积分的响应等于原输入响应的积分J' x(0)dt -→ J' y(0)dt(1-5)5、频率保持性稳态条件下，系统输出的频率与输入的频率保持一致若x(t) = X sin( ot +0)(1-6)y()=Ysin(ot +0,)则严格讲，工程实际应用的测试系统不可能在整个工作范围内完全保持线性，只能在一定范围内和一定（误差）条件下作线性处理，视为线性系统。本书仅限于线性系统来讨论。研究测试系统的输入输出关系，实际上就是研究系统对外呈现的外部特性，它由其内部参数以及系统本身的固有特性所决定。如果测试系统的输入x()不随时间变化，或随时间变化程度远远缓慢于系统固有的最低阶运动模式的变化程度时，测试系统的基本特性可称为静态特性，反之，称为动态特性。-2

一-2 ( ) ( ) (1 5) 0 0 → −   t t x t dt y t dt 二、线性测试系统及其基本特性 如果测试系统的输出、输入具有单值对应的线性关系，则称为线性测试系统。设系统的 输入为 x(t)，输出为 y(t)，则它们可用线性微分方程来表示： 式中 a0, a1, a2, ┅, an 和 b0, b1, b2,┅,bn 是与测量装置特性和输入状况有关的常数，它们既不 随时间变化，也不是自变量 x 、因变量 y 及它们各阶导数的函数。 若以 x(t)—→y(t)表示线性系统的输入、输出关系，则具有以下主要性质： 1、叠加特性 符合叠加原理 若 x1(t) —→y1(t)， x2(t) —→y2(t)， 则 [x1(t) ± x2(t)] —→[y1(t) ± y1(t)] （1-2） 2、比例特性 对于任意常数 a，有 ax(t) —→ay(t) （1-3） 3、微分特性 对输入微分的响应等于对原输入响应的微分 4、 积分特性 系统初始状态为零条件下，对输入积分的响应等于原输入响应的积分 5、频率保持性 稳态条件下，系统输出的频率与输入的频率保持一致 若 则 严格讲，工程实际应用的测试系统不可能在整个工作范围内完全保持线性，只能在一定 范围内和一定（误差）条件下作线性处理，视为线性系统。本书仅限于线性系统来讨论。 研究测试系统的输入输出关系，实际上就是研究系统对外呈现的外部特性，它由其内部 参数以及系统本身的固有特性所决定。如果测试系统的输入 x(t) 不随时间变化，或随时间 变化程度远远缓慢于系统固有的最低阶运动模式的变化程度时，测试系统的基本特性可称为 静态特性，反之，称为动态特性。 ( ) (1 1) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 1 0 1 1 1 1 0 1 1 = + + + + − + + + + − − − − − − b x t dt dx t b dt d x t b dt d x t b a y t dt dy t a dt d y t a dt d y t a m m m m m m n n n n n n   (1 4) ( ) ( ) → − dt dy t dt dx t ( ) sin( ) x x t = X t + ( ) = sin( + ) (1− 6) y y t Y t 

第二节测量装置的静态特性一、静态特性的标定静态测试时，线性微分方程中各阶导数均为零，于是式（1-1）就变为J0-x()-5()(1-7)式中 S=邹为常量它是理想的定常线性测量系统的静态特性的表达式。而实际的测量系统不可能是完全的线性系统，其输入与输出关系一般不是定常关系，这时可用多项式来表示(1-8)y)=S +$+)+$,()+.要确定测量装置的静态特性，就需要对测量装置进行标定。静态特性标定就是在规定的测试条件下，对测量装置输入一系列一致的、准确的、不随时间变化的高精度输入量，同时用高精度测量仪器测定被标定装置对应的输出量，然后根据输入、输出量值，通过一定的方法得出输入一输出特性曲线。二、灵敏度在稳定工作状态下，测量装置输出信号的变化量Ay与引起此变化的输入信号的变化量Ax之比，称为该装置的灵敏度，记作SS=%(1-9)由多个测试环节组成的测试系统，其灵敏度是系统最终输出的变化量与最初输入变化量的比值。如果已知各测量环节的灵敏度，可用其乘积来表示，即S=S,.S, S,..(1-10)式中S.-—传感器的灵敏度；S,·S.…一其它各测量环节的灵敏度。-某一点的静态灵敏度就是其静态特性曲线的斜率。线性系统的灵敏度为一常数，而非线性系统的灵敏度是个变量。灵敏度的单位为输出量和输入量单位之比。但如果输出量和输入量单位相同，则灵敏度为一个无量纲的比例常数，称之为“放大倍数”或“增益”。-3

一-3 第二节 测量装置的静态特性 一、静态特性的标定 静态测试时，线性微分方程中各阶导数均为零，于是式（1-1）就变为 ( ) ( ) ( ) (1 7) 0 0 = x t = Sx t − a b y t 式中 0 0 a b S = 为常量 它是理想的定常线性测量系统的静态特性的表达式。而实际的测量系统不可能是完全的线性 系统，其输入与输出关系一般不是定常关系，这时可用多项式来表示 ( ) ( ) ( ) (1 8) 2 y t = S0 + S1 x t + S2 x t + − 要确定测量装置的静态特性，就需要对测量装置进行标定。 静态特性标定就是在规定的测试条件下，对测量装置输入一系列一致的、准确的、不随 时间变化的高精度输入量，同时用高精度测量仪器测定被标定装置对应的输出量，然后根据 输入、输出量值，通过一定的方法得出输入—输出特性曲线。 二、灵敏度 在稳定工作状态下，测量装置输出信号的变化量 y 与引起此变化的输入信号的变化量 x 之比，称为该装置的灵敏度，记作 S (1−9)   = x y S 由多个测试环节组成的测试系统，其灵敏度是系统最终输出的变化量与最初输入变化量 的比值。如果已知各测量环节的灵敏度，可用其乘积来表示，即 (1 10) S = S1  S2  S3  − 式中 1 S ——传感器的灵敏度； S2  S3  ——其它各测量环节的灵敏度。 某一点的静态灵敏度就是其静态特性曲线的斜率。线性系统的灵敏度为一常数，而非线 性系统的灵敏度是个变量。 灵敏度的单位为输出量和输入量单位之比。但如果输出量和输入量单位相同，则灵敏度 为一个无量纲的比例常数，称之为“放大倍数”或“增益

提高系统的灵敏度，会使输出信号增强，但灵敏度太高，则稳定性变差，测量范围变小所以，一个测试系统，不能片面追高灵敏度，而要兼顾系统的抗干扰能力和稳定性。三、 分辨力与分辨率当测量装置的输入量变化太小时，输出量的变化无法分辨。于是，将测量装置有效地辨别输入量最小变化量的能力称为分辨力。一般认为，数字仪表的分辨力是其显示的最后位数的变化值，模拟装置的分辨力为指示标尺分度值的一半。分辨力受仪器或装置的噪声电平限制，只有当信号电平高于噪声电平定倍数（一般认为信噪比高于5dB）时，显示值才有意义。分辨率是指分辨力与整个测量范围的百分比，即Ar.x100%(111)=X-X式中r--分辨率，Arm分辨力，Xmx-最大输入量，Xmn--最小输入量分辨力反映了测量装置检测输入微小变化的能力，对正反行程都是适用的。分辨率则表明测量装置的相对分辨能力。影响分辨力的因素很多，如电路中的储能元件、A/D变换位数、机械运动部件的摩擦等。四、线性度由式（1-7）描述的测量装置的静态特性是一条直线。但由于种种原因，工程实际中的测量装置不可能完全保持线性关系，即存在非线性。习惯上，用非线性误差来表示线性指标，即线性度。线性度是指测量装置的标定曲线与其理想直线（或拟合直线）的最大不重合程度。工程上，通常是用标定的方法得到一条标定曲线，并由此拟合出标定直线（图1-2）。在标称图1-2线性度1一最小二乘拟合直线输出范围内，标定曲线与其拟合直线的最大偏差B与满量程2一实测定度曲线输出比值的百分率称为线性度，即IBIx100%L:(112)Ymx - ymin式中L.--.线性度x---最大输出值Yx---最小输出值（可以为负值）

一-4 提高系统的灵敏度，会使输出信号增强，但灵敏度太高，则稳定性变差，测量范围变小。 所以，一个测试系统，不能片面追高灵敏度，而要兼顾系统的抗干扰能力和稳定性。 三、分辨力与分辨率 当测量装置的输入量变化太小时，输出量的变化无法分辨。于是，将测量装置有效地辨 别输入量最小变化量的能力称为分辨力。 一般认为，数字仪表的分辨力是其显示的最后位数的变化值，模拟装置的分辨力为指示 标尺分度值的一半。分辨力受仪器或装置的噪声电平限制，只有当信号电平高于噪声电平一 定倍数（一般认为信噪比高于 5dB）时，显示值才有意义。 分辨率是指分辨力与整个测量范围的百分比，即 100% (1 11) max min min  − −  = x x x r 式中 r -分辨率， min x -分辨力， max x -最大输入量， min x -最小输入量 分辨力反映了测量装置检测输入微小变化的能力，对正反行程都是适用的。分辨率则表 明测量装置的相对分辨能力。影响分辨力的因素很多，如电路中的储能元件、A/D 变换位数、 机械运动部件的摩擦等。 四、线性度 由式（1-7）描述的测量装置的静态特性是一条直线。 但由于种种原因，工程实际中的测量装置不可能完全保持线 性关系，即存在非线性。习惯上，用非线性误差来表示线性 指标，即线性度。 线性度是指测量装置的标定曲线与其理想直线（或拟合 直线）的最大不重合程度。工程上，通常是用标定的方法得 到一条标定曲线，并由此拟合出标定直线（图 1-2）。在标称 输出范围内，标定曲线与其拟合直线的最大偏差 B 与满量程 输出比值的百分率称为线性度，即 100% (1 12) | | max min  − − = y y B L 式中 L-线性度 max y -最大输出值 max y -最小输出值（可以为负值） 图 1-2 线性度 1— 最小二乘拟合直线 2— 实测定度曲线

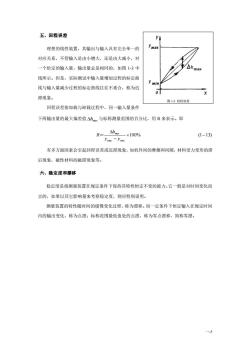
五、回程误差yyma理想的线性装置，其输出与输入具有完全单一的对应关系，不管输入是由小增大，还是由大减小，对一个给定的输入量，输出量总是相同的，如图1-3中线所示。但是，实际测试中输入量增加过程的标定曲线与输入量减少过程的标定曲线往往不重合，称为迟滞现象。图1-3回程误回程误差指加载与卸载过程中，同一输入量条件下两输出量的最大偏差值Ahmx与标称测量范围的百分比，用R来表示。即Ah.(113)×100%Ymex- Ymin有多方面因素会引起回程误差或迟滞现象，如机件间的摩擦和间隙，材料受力变形的滞后现象，磁性材料的磁滞现象等。六、稳定度和漂移稳定度是指测量装置在规定条件下保持其特性恒定不变的能力。它一般是对时间变化而言的，如果以其它影响量来考察稳定度，则应特别说明测量装置的特性随时间的缓慢变化过程，称为漂移。而一定条件下恒定输入在规定时间内的输出变化，称为点漂；标称范围最低值处的点漂，称为零点漂移，简称零漂

一-5 五、回程误差 理想的线性装置，其输出与输入具有完全单一的 对应关系，不管输入是由小增大，还是由大减小，对 一个给定的输入量，输出量总是相同的，如图 1-3 中 线所示。但是，实际测试中输入量增加过程的标定曲 线与输入量减少过程的标定曲线往往不重合，称为迟 滞现象。 回程误差指加载与卸载过程中，同一输入量条件 下两输出量的最大偏差值 hmax 与标称测量范围的百分比，用 R 来表示。即 100% (1 13) max min max  − −  y y h R＝ 有多方面因素会引起回程误差或迟滞现象，如机件间的摩擦和间隙，材料受力变形的滞 后现象，磁性材料的磁滞现象等。 六、稳定度和漂移 稳定度是指测量装置在规定条件下保持其特性恒定不变的能力。它一般是对时间变化而 言的，如果以其它影响量来考察稳定度，则应特别说明。 测量装置的特性随时间的缓慢变化过程，称为漂移。而一定条件下恒定输入在规定时间 内的输出变化，称为点漂；标称范围最低值处的点漂，称为零点漂移，简称零漂。 图 1-3 回程误差

第三节测量装置的动态特性当被测参数随时间变化时，测量装置处于动态测量状态。则动态特性指动态测量时，测量装置的输出量与被测输入量之间随时间变化的函数关系。在动态测量情况下，测量装置的输入、输出关系除与静态特性有关外，还受动态特性影响。且动态特性不仅取决于测量装置的结构，而且还与输入信号有关。所以描述测量装置的动态特性，实质上就是建立输入信号、输出信号和测量装置三者之间的关系。通常用测量装置的传递函数、频率相应函数和脉冲相应函数来描述测量装置的动态传递特性。三者从不同角度表示出测量装置的动态特性，它们之间既互相联系又各有其特点。一、传递函数若测量装置处于零初始条件，即当1≤0时，输入信号x()、输出信号y()及其各阶导数均为零，则对式（1-1）进行拉普拉斯变换，可得：(a,s" +a-s"- +.+ais+ao)Y(s)=(b.s" +b.-ism- +..+b,s+bo)X(s)则Y(s) _ bms"+b-s"++bys+bo(1-14)X()a,sa-".a+a式中an、an-1、*、ar、ao和bm、bm-1、、bi、bo均是由测量装置确定的常数。式（1-14)是测量装置传递特性的一种表达式。为此，将初始条件为零时，输出信号和输入信号的拉普拉斯变换之比称为测量装置的传递函数 H(s)，即O-10(1-15) Y(s)= I, y(0)e"dy(t)x(tX(s) = x(0)e" dtX(s)H(a)Y(s)式中Y(s)——输出信号y()的拉普拉斯变换；输入输出图 1-4 测试系统、输入与输出三者关系X(s)——输入信号x()的拉普拉斯变换；——拉普拉斯算子，S=α+joα和o皆为实变量）(α>0,--6

一-6 第三节 测量装置的动态特性 当被测参数随时间变化时，测量装置处于动态测量状态。则动态特性指动态测量时，测 量装置的输出量与被测输入量之间随时间变化的函数关系。在动态测量情况下，测量装置的 输入、输出关系除与静态特性有关外，还受动态特性影响。且动态特性不仅取决于测量装置 的结构，而且还与输入信号有关。所以描述测量装置的动态特性，实质上就是建立输入信号、 输出信号和测量装置三者之间的关系。通常用测量装置的传递函数、频率相应函数和脉冲相 应函数来描述测量装置的动态传递特性。三者从不同角度表示出测量装置的动态特性，它们 之间既互相联系又各有其特点。 一、传递函数 若测量装置处于零初始条件，即当 t ≤0 时，输入信号 x(t) 、输出信号 y(t) 及其各阶导 数均为零，则对式（1-1）进行拉普拉斯变换，可得： ( ) ( ) ( ) ( ) 1 0 1 1 1 0 1 1 b s b s b s b X s a s a s a s a Y s m m m m n n n n = + + + + + + + + − − − −   则 (1 14) ( ) ( ) 1 0 1 1 1 0 1 1 − + + + + + + + + = − − − − a s a s a s a b s b s b s b X s Y s n n n n m m m m   式中 an、an-1、.、a1、a0 和 bm、bm-1、.、b1、b0 均是由测量装置确定的常数。式（1-14） 是测量装置传递特性的一种表达式。为此，将初始条件为零时，输出信号和输入信号的拉普 拉斯变换之比称为测量装置的传递函数 H(s) ，即 (1 15) ( ) ( ) ( ) = − X s Y s H s    −  − = = 0 0 ( ) ( ) ( ) ( ) X s x t e dt Y s y t e dt st st 式中 Y(s)——输出信号 y(t)的拉普拉斯变换； X(s)——输入信号 x(t)的拉普拉斯变换； s——拉普拉斯算子， s = + j (  0, 和皆为实变量） 输入 输出 图 1-4 测试系统、输入与输出三者关系 x(t) X(s) Y(s) y(t)

传递函数表示测量装置的输入信号与输出信号之间在复数域内的关系（图1-4)），它有如下特点：1、H(s)描述系统本身的固有特性，与输入信号x()的类型无关。x()不同时，y(t)也不同，但二者拉普拉斯变换的比值H(s)保持不变。2、H(s)反映测量装置的传输、转换和响应特性，与具体物理结构无关。同一形式的传递函数可以表征具有相同传输特性的不同物理系统2、H(s)起传递作用，只要知道X(s)、Y(s)、H(s)三者中的任意两个，则可以很方便地求出第三者。二、频率响应函数若能在频域中研究测量装置对任意输入的响应，则将有可能简化研究过程。为此，将s-j@代入（1-14)，就可得到Y(jo)_ b.(Go)*+b.(jo)++b(jo)+b.(116)X(jo) .,(jo)+.(jo)*+,(o)+.o对比复数域传递函数的定义，可得测量装置在频域的传递函数，称为频率响应函数（简称频响函数)，即- (1-17)式中Ya)——输出信号y(的傅氏变换，Y(jo)=y()e-adt；XG)——输出信号x(0的傅氏变换；X(jo)=x(1)e-adt用频响函数来描述系统的最大优点是它可以通过实验求得。即依次用不同频率の，的简谐信号去激励被测装置，同时测得激励（输入）和装置的稳态输出幅值%i、6和相位差9。Yoi这样对于某个の，便有一=4和9，全部的4-0和9-0（=1,2），便可表To达测量装置的频率响应函数。三、脉冲响应函数若输入为单位脉冲8()（图1-5a)，即x(0=8(t),则其拉氏变换X(s)=L[6(1)=1。根据式(1-15),测量装置的相应输出将是Y(s)=H(s)X(s)=H(s),其时域描述可以通过对 Y(s)-7

一-7 传递函数表示测量装置的输入信号与输出信号之间在复数域内的关系（图 1-4），它有 如下特点： 1、H(s)描述系统本身的固有特性，与输入信号 x(t) 的类型无关。x(t)不同时，y(t)也不 同，但二者拉普拉斯变换的比值 H(s)保持不变。 2、H(s)反映测量装置的传输、转换和响应特性，与具体物理结构无关。同一形式的传 递函数可以表征具有相同传输特性的不同物理系统。 2、H(s)起传递作用，只要知道 X(s)、Y(s)、H(s)三者中的任意两个，则可以很方便地求 出第三者。 二、频率响应函数 若能在频域中研究测量装置对任意输入的响应，则将有可能简化研究过程。为此，将 s=jω代入（1-14），就可得到 (1 16) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 0 1 1 1 0 1 1 − + + + + + + + + = − − − − a j a j a j a b j b j b j b X j Y j n n n n m m m m           对比复数域传递函数的定义，可得测量装置在频域的传递函数，称为频率响应函数(简称频 响函数)，即 (1 17) ( ) ( ) ( ) = −    X j Y j H j 式中 Y(jω)——输出信号 y(t)的傅氏变换，   − = 0 Y( j ) y(t)e dt jt  ； X(jω)——输出信号 x(t)的傅氏变换；   − = 0 X( j ) x(t)e dt jt  用频响函数来描述系统的最大优点是它可以通过实验求得。即依次用不同频率 i 的简 谐信号去激励被测装置，同时测得激励（输入）和装置的稳态输出幅值 X0i、Y0i 和相位差 i 。 这样对于某个 i ，便有一组 i i i A X Y = 0 0 和  i ，全部的 Ai −i 和 i −i (i=1,2,.)，便可表 达测量装置的频率响应函数。 三、脉冲响应函数 若输入为单位脉冲δ(t)（图 1-5a），即 x(t)= δ(t)，则其拉氏变换 X(s) = L (t) =1。 根据式（1-15），测量装置的相应输出将是 Y(s)=H(s)X(s)=H(s)，其时域描述可以通过对 Y(s)

的拉普拉斯反变换得到，即(0) = L-[H(s)] = h(0) (118)h(t)称为测量装置的脉冲响应函数或权函数（图1-5b）。脉冲响应函数可作为系统特性的时域描述。综上所述，系统特性在时域可用脉冲响应函数h()来描述，在频域可用频率响应函数 HG)来描述，在复数域可-5单位脉冲和脉冲响应函用传递函数 H(s)来描述。三者的关系也是一对应的。脉冲响应函数 h()和传递函数 H(s)是一个拉普拉斯变换对，h()与频率响应函数H(）是一个傅氏变换对。四、环节的串联和并联如果测试系统是由两个环节串联而成（图1-6)，它们的传递函数分别为Hi(s)和 H(s)，则该串联系统的传递函数为_ Y() - ZY = H(S)H(s)H(s)=(1-19) X(s)X(s) Z(s)可以推出，若测试系统有多个环节串联而成，其总的传递函数为H(s)= H(s)H,(s)..H,(s)- IIH(s)(120)如果测试系统有两个环节并联而成（图1-7)，它们的传递函数分别为H,(s)和H,(s)，则该并联系统的传递函数为--+-H()+H()H(s) =(1-21)X()" X(s) +X(s)由此可推出，多个环节并联而成的测试系统，总的传递函数为H(s)= H;(s)+H,(s)+H,(s)=2h,(s)(122) 同样，令s-jo代入式（1-20）和式（1-22）得到n个环节串联系统频响函数为H(0)=IIH(o)(I-23) -8

一-8 的拉普拉斯反变换得到，即 ( ) [ ( )] ( ) (1 18) 1 = = − − y t L H s h t h(t)称为测量装置的脉冲响应函数或权 函数(图 1-5b)。脉冲响应函数可作为系 统特性的时域描述。 综上所述，系统特性在时域可用脉 冲响应函数 h(t)来描述，在频域可用频 率响应函数 H(jω)来描述，在复数域可 用传递函数 H(s)来描述。三者的关系也是一一对应的。脉冲响应函数 h(t)和传递函数 H(s) 是一个拉普拉斯变换对，h(t)与频率响应函数 H(ω)是一个傅氏变换对。 四、环节的串联和并联 如果测试系统是由两个环节串联而成（图 1-6），它们的传递函数分别为 H1(s)和 H2(s)， 则该串联系统的传递函数为 ( ) ( ) (1 19) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = =  = H1 s H2 s − Z s Y s X s Z s X s Y s H s 可以推出，若测试系统有多个环节串联而成，其总的传递函数为 ( ) ( ) ( ) ( ) ( ) (1 20) 1 = 1 2 =  − = n i n i H s H s H s H s H s 如果测试系统有两个环节并联而成（图 1-7），它们的传递函数分别为 ( ) 1 H s 和 ( ) 2 H s ， 则该并联系统的传递函数为 ( ) ( ) (1 21) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 2 1 2 = = + = H s + H s − X s Y s X s Y s X s Y s H s 由此可推出，多个环节并联而成的测试系统，总的传递函数为 ( ) ( ) ( ) ( ) ( ) (1 22) 1 = 1 + 2 + + =  − = n i n i H s H s H s  H s H s 同样，令 s=jω代入式（1-20）和式（1-22）得到 n 个环节串联系统频响函数为 ( ) ( ) (1 23) 1 =  − = n i H  Hi  1-5 单位脉冲和脉冲响应函数

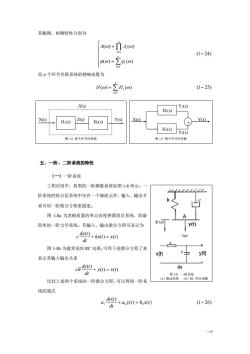
其幅频、相频特性分别为A(0)=I/4(0)(1-24)Zg,(0)而n个环节并联系统的频响函数为H(0)=ZH,(o)(125)H(s)Y1(s)Hi(s)X(s)(S)H(s)X(s)Hi(s)H2(s)Y2(S)图1-6两个环节的串联图1-7两个环节的并联五、一阶、二阶系统的特性(一）一阶系统工程应用中，典型的一阶测量系统如图1-8所示阶系统的特点是系统中仅有一个储能元件，输入、输出关k<系可用一阶微分方程来描述。图1-8a为忽略质量的单自由度弹簧阻尼系统，即最X4[y(t)简单的一阶力学系统。其输入、输出微分方程可表示为d() + ky(0)= x()(a)图1-8b为最常见的RC电路，可用下述微分方程了来十y(t)x(t)表示其输入输出关系cR ≤ + () =x)(b)1() 显联线一的系能 积分电路比较上述两个系统的一阶微分方程，可以得到一阶系统的通式 + ao)()= box()( 26) 1dt

一-9 其幅频、相频特性分别为 (1 24) ( ) ( ) ( ) ( ) 1 1 −        = =   = = n i i n i A Ai       而 n 个环节并联系统的频响函数为 ( ) ( ) (1 25) 1 =  − = n i H  Hi  五、一阶、二阶系统的特性 （一）一阶系统 工程应用中，典型的一阶测量系统如图 1-8 所示。一 阶系统的特点是系统中仅有一个储能元件，输入、输出关 系可用一阶微分方程来描述。 图 1-8a 为忽略质量的单自由度弹簧阻尼系统，即最 简单的一阶力学系统。其输入、输出微分方程可表示为 ( ) ( ) ( ) ky t x t dt dy t c + = 图 1-8b 为最常见的 RC 电路，可用下述微分方程了来 表示其输入输出关系 ( ) ( ) ( ) y t x t dt dy t cR + = 比较上述两个系统的一阶微分方程，可以得到一阶系 统的通式 ( ) ( ) (1 26) ( ) 1 + a0 y t = b0 x t − dt dy t a H(s) X(s) Z(s) Y(s) 图 1-6 两个环节的串联 图 1-7 两个环节串连 H1(s) H2(s) Y1(s) X(s) Y(s) Y2(s) 图 1-7 两个环节的并联 H1(s) H2(s) + 图 1-8 一阶系统 （a）振动系统 （b）RC 积分电路

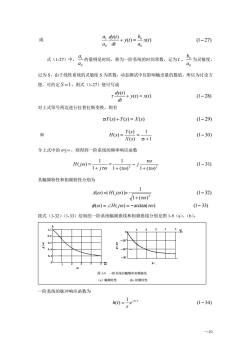
+ (0)=x()或(127)aodtbo为灵敏度，"的量纲是时间，称为一阶系统的时间常数，记为T。式（1-27）中记为S，由于线性系统的灵敏度s为常数，动态测试中仅影响输出量的数值，所以为讨论方便，可约定S=1，则式（1-27）便可写成 + y(0)= x()(28)dt对上式等号两边进行拉普拉斯变换，则有Y(s)+Y(s) = X(s)(1-29)H(s)= Y() _和(130)X(s)$+1令上式中的sjo，则得到一阶系统的频率响应函数TOH(jo)=(1-31)+ jto1+(to)?1+(t0)2其幅频特性和相频特性分别为(1 32) A(o)= H(jo)=-/1+(to)?(1-33)(o) = ZH(jo) = -arctan( to)按式（1-32）（1-33）绘制的一阶系统幅频曲线和相频曲线分别见图1-9（a)、（b)。:图1-9一阶系统的幅频和相频曲线（a）幅频特性(b)相频特性一阶系统的脉冲响应函数为ho -1e":(134)--10

一-10 或 ( ) ( ) (1 27) ( ) 0 0 0 1 + = x t − a b y t dt dy t a a 式（1-27）中， 0 1 a a 的量纲是时间，称为一阶系统的时间常数，记为  。 0 0 a b 为灵敏度， 记为 S，由于线性系统的灵敏度 S 为常数，动态测试中仅影响输出量的数值，所以为讨论方 便，可约定 S =1 ，则式（1-27）便可写成 ( ) ( ) (1 28) ( ) + y t = x t − dt dy t  对上式等号两边进行拉普拉斯变换，则有 sY(s) +Y(s) = X(s) (1− 29) 和 (1 30) 1 1 ( ) ( ) ( ) − + = = X s s Y s H s  令上式中的 s=jω，则得到一阶系统的频率响应函数 (1 31) 1 ( ) 1 ( ) 1 1 1 ( ) 2 2 − + − + = + =      j j H j 其幅频特性和相频特性分别为 ( ) ( ) arctan( ) (1 33) (1 32) 1 ( ) 1 ( ) | ( ) | 2 =  = − − − + = =        H j A H j 按式（1-32）（1-33）绘制的一阶系统幅频曲线和相频曲线分别见图 1-9（a）、（b）。 一阶系统的脉冲响应函数为 (1 34) 1 ( ) / = − −   t h t e 图 1-9 一阶系统的幅频和相频曲线 （a）幅频特性 (b) 相频特性