《机械控制工程基础》课程教学资源（PPT课件）第二章 控制系统的数学模型

常见函数的Laplace变换 1(t) 2 t> 口3 e at 1 s+a 4 O Snot→ s2+02 5 S cos wt s2+ 2

常见函数的Laplace变换  1  2  3  4  5 s t 1 1( ) → 2 1 s t → s a e at + − → 1 2 2 sin    + → s t 2 2 cos   + → s s t

第二章控制系统的数学模型 口线性系统：系统的数学模型能用 线性微分方程描述。 口线性定常系统：微分方程的系数 为常数。 口线性系统满足叠加原理。 建立数学模型的方法：分析法和 实验法

线性系统：系统的数学模型能用 线性微分方程描述。 线性定常系统：微分方程的系数 为常数。 线性系统满足叠加原理。 建立数学模型的方法：分析法和 实验法。 第二章控制系统的数学模型

2.1控制系统的微分方程 一 列写微分方程的一般方法 列写系统（或元件）的微分方程，目 的在于确定系统的输出量与给定输入量或 扰动输入量之间的函数关系。 口确定系统（或元件）的输入量和输出量 口从系统输入端开始，列写各个环节的动态微分方程 口消除中间变量，得出输入输出之间关系的微分方程 整理得出微分方程

 确定系统（或元件）的输入量和输出量  从系统输入端开始，列写各个环节的动态微分方程  消除中间变量，得出输入输出之间关系的微分方程  整理得出微分方程 2.1控制系统的微分方程 一 列写微分方程的一般方法 列写系统（或元件）的微分方程，目 的在于确定系统的输出量与给定输入量或 扰动输入量之间的函数关系

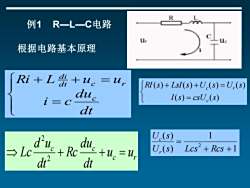
例1R一L一C电路 根据电路基本原理 Ri+Ldi+ue =ur RI(s)+LsI(s)+U(s)=U,(s) i=C due I(s)=csU(s) dt U.(s) 1 +R →Lc- du ur U(s) Lcs2+Rcs+1 r

例1 R—L—C电路     = + + = dt du i c Ri L u u c dt c r di c r c c u u dt du Rc dt d u  Lc + + = 2 2 根据电路基本原理    = + + = ( ) ( ) ( ) ( ) ( ) ( ) I s csU s RI s LsI s U s U s c c r 1 1 ( ) ( ) 2 + + = U s Lcs Rcs U s r c

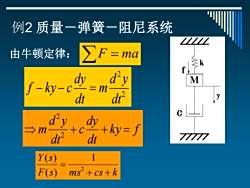
例2质量一弹簧一阻尼系统 由牛顿定律： ∑F=ma f-ky- dy二 d dt d m ay+c dr 内+y=∫ 77777 Y(s) F(s) ms+cs+k

例2 质量－弹簧－阻尼系统 由牛顿定律： F = ma 2 2 dt d y m dt dy f − k y − c = k y f dt dy c dt d y  m + + = 2 2 F s ms cs k Y s + + = 2 1 ( ) ( )

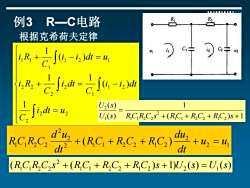
例3R一C电路 R R2 根据克希荷夫定律 4R:+C.5(-1)de =m 6R+Gj6h=C∫-h ∫，=4 U2(S) 1 U(s) RCRC2s2+(RC+RC2+RC2)s+1 RC R2C2 du+(RC+RC:+RC:) d2+u2=4 (RC RC2s2+(RC+RC,+RC2)s+1U2(S)=U(s)

         = + = − + − =     2 2 2 1 2 1 2 2 2 2 1 2 1 1 1 1 1 ( ) 1 1 ( ) 1 i dt u C i i dt C i dt C i R i i dt u C i R 例3 R—C电路 根据克希荷夫定律 2 1 2 2 1 1 2 2 1 2 2 2 1 1 2 2 ( ) u u dt du R C R C R C dt d u R C R C + + + + = ( ( ) 1) ( ) ( ) 1 1 2 2 1 2 2 1 2 1 1 2 2 R C R C s + R C + R C + R C s + U s = U s ( ) 1 1 ( ) ( ) 1 1 2 2 1 2 2 1 1 1 2 2 2 + + + + = U s R C R C s R C R C R C s U s

若孤立地分别写出两个环节的微分方程，则 t=4 C.Jid-u C.Sid-w RCRC2 u+(RC+RC: d2+u2=4, dt (RCRC2s+(RC]+RC2)s+1U2(s)=U(s) 这就是负载效应的结果。 负载效应就是物理环节之间的信息反馈作用

若孤立地分别写出两个环节的微分方程，则        = + =    1 2 1 1 1 1 1 1 1 1 i dt u C i dt u C i R        = + =    2 2 2 2 2 2 2 2 1 1 i dt u C i dt u C i R 2 1 2 2 1 1 2 2 2 2 1 1 2 2 ( ) u u dt du R C R C dt d u R C R C + + + = ( ( ) 1) ( ) ( ) 1 1 2 2 2 1 2 1 1 2 2 R C R C s + R C + R C s + U s =U s 这就是负载效应的结果。 负载效应就是物理环节之间的信息反馈作用

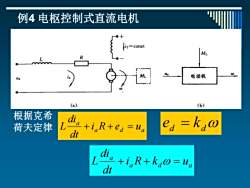
例4电枢控制式直流电机 =const M 电动机 (a) (b) 根据克希 荷夫定律 +iR+ed =ua ed dt dt +i R+kao=ud

例4 电枢控制式直流电机 根据克希 荷夫定律 a d a a i R e u dt di L + + = ed = kd  a d a a i R k u dt di L + +  =

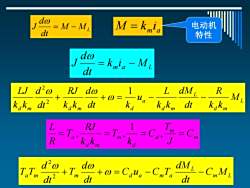
M-M M=kia 电动机 dt 特性 do dt =kmia -M. LJ d"o RJ do 1 +0= L dM R kakm dt2 kakn dt dt kakm m +o=Cqu-CuT dt dMLC M dt

M M L dt d J = −  m a M = k i m a M L k i dt d J = −  L d m L d m a d m d m d M k k R dt dM k k L u dt k d k k RJ dt d k k LJ + + = − − 1 2 2    m m d d m d m a C J T C k T k k RJ T R L = = = , = 1 , , m L L a m m d a m a C M dt dM C u C T dt d T dt d T T + + = − −   2 2 电动机 特性

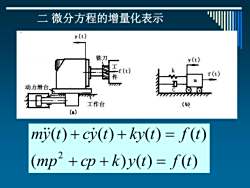
二微分方程的增量化表示 y(t) 铣刀 y(t) (t) f(t) 动力滑台 工作台 (b) (a) mi(t)+ci(t)+ky(t)=f(t) (mp2+cp+k)y(t)=f(t)

二 微分方程的增量化表示 ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 mp cp k y t f t my t cy t ky t f t + + =  +  + =