《机械控制工程基础》课程基础习题（无答案）

第一章 1.试比较开环控制系统和闭环控制系统的优缺点。 2.如题图1-1(a)、(b)所示两水位控制系统，要求： 画出方块图（包括给定输入量和扰动输入量）： ·分析工作原理，讨论误差和扰动的关系。 进 O ☒减速器 放大器电动机 用户 (b) 图1-1 3.如题图1-2所示炉温控制系统，要求(1)指出系统输出量、给定输入量、扰动输入量 被控对象和自动控制器的各组成部分并画出方块图：(2)说明该系统是怎样得到消除或减少 偏差的。 十 功率 信号 放大 n 电机 220 图1-2 4.举出五个身边控制系统的例子，试用职能方块图说明其基本原理，并指出是开环还是闭环。 5.双输入控制系统的一个常见例子是由冷热两个阀门的家用沐浴器。目标是同时控制水温和 流量，画出此闭环系统的方块图，你愿意让别人给你开环控制的沐浴器吗？

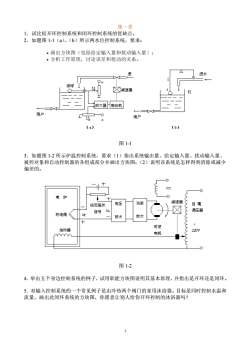
1 第一章 1．试比较开环控制系统和闭环控制系统的优缺点。 2．如题图 1-1（a）、（b）所示两水位控制系统，要求： • 画出方块图（包括给定输入量和扰动输入量）； • 分析工作原理，讨论误差和扰动的关系。 图 1-1 3．如题图 1-2 所示炉温控制系统，要求（1）指出系统输出量、给定输入量、扰动输入量、 被控对象和自动控制器的各组成部分并画出方块图；（2）说明该系统是怎样得到消除或减少 偏差的。 图 1-2 4．举出五个身边控制系统的例子，试用职能方块图说明其基本原理，并指出是开环还是闭环。 5．双输入控制系统的一个常见例子是由冷热两个阀门的家用沐浴器。目标是同时控制水温和 流量，画出此闭环系统的方块图，你愿意让别人给你开环控制的沐浴器吗？

第二章 1.试求下列函数的拉氏变换 (1)f)=(4r+5)6)+(t+2)1) 2f0=6s31-45)-1u-至 (3)f)=e6(cos8+0.25sin8 2.试求下列函数的拉氏反变换 1)FS)=5+2Xs+3) s+1 (2)F(S)= s-1 (3)FS=5+Ds+2 4 (4)FS)=+5+4 3.对题图21所示的控制系统，计算()，（⑨」 H3() R()+ G(⊙ 0,(c H() 图2-1 4,系统结构如题图2,2所示。试分别用结构图化简方法和梅逊公式法求传递函数C心)/R R附 G⊙ g2)G(⑨ 图2-2 5.系统结构图如题图2-3所示。求传递函数C)/R份及8)/

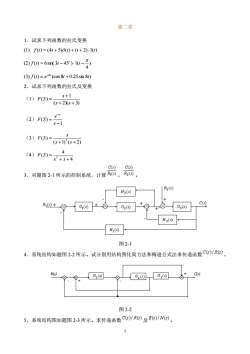
2 第二章 1．试求下列函数的拉氏变换 (1) f (t) = (4t + 5) (t) + (t + 2)1(t) (2) ) 4 ( ) 6sin( 3 45 ) 1(  f t = t −  t −  (3) ( ) (cos8 0.25sin 8 ) 6 f t e t t t = + − 2．试求下列函数的拉氏反变换 （1） ( 2)( 3) 1 ( ) + + + = s s s F S （2） 1 ( ) − = − s e F S s （3） ( 1) ( 2) ( ) 2 + + = s s s F S （4） 4 4 ( ) 2 + + = s s F S 3．对题图 2-1 所示的控制系统，计算 ， 。 图 2-1 4．系统结构如题图 2-2 所示。试分别用结构图化简方法和梅逊公式法求传递函数 。 图 2-2 5．系统结构图如题图 2-3 所示。求传递函数 及

型g ,型 图2-3 6.试列写题图2-4所示双输入-双输出机械位移系统的微分方程并画出系统结构图。 图2-4 第三章 C(s）+b 1,考虑一个单位反馈控制系统，其闭环传递函数为 R(s)s2+as+b (1)试确定其开环传递函数G()。 (2)求单位斜坡输入时的稳态误差。 2.已知单位反馈系统的单位阶跃响应为0=1+02。-12.,求 (1)开环传递函数G: (2)50w5,:

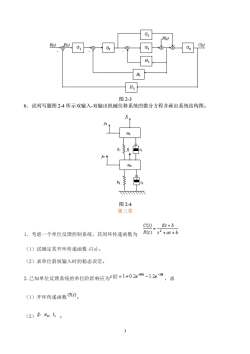
3 图 2-3 6．试列写题图 2-4 所示双输入-双输出机械位移系统的微分方程并画出系统结构图。 图 2-4 第三章 1．考虑一个单位反馈控制系统，其闭环传递函数为 （1）试确定其开环传递函数 G(s)。 （2）求单位斜坡输入时的稳态误差。 2.已知单位反馈系统的单位阶跃响应为 ，求 （1）开环传递函数 ； （2） ；

(3)在0-2+242作用下的稳态误差。 3.设单位反债整制系统的开环传递通数为9~G,4网。已知系统在单位阶跃作用下的 误差响应为)-2e-,试求系统的阻尼比5，自然须率，和在单位斜坡输入作用下的稳 态误差。 4.设题图3-1()所示系统的单位阶跃响应曲线如图3-1(b)所示，试确定参数1、2和 a的数值。 21810 2.00 附图 C sis+a) 08 b 题图3-1 5.设复合控制系统如题图3-2所示，要求： (1)计算扰动n(t)=t引起的稳态误差： (2)设计C,使系统在r(t)=t作用下无稳态误差。 K: N( t) K3 图3-2 6.己知系统结构如题图3-3所示，试求：当r(t)=t,n(t)=1(t)时的稳态误差

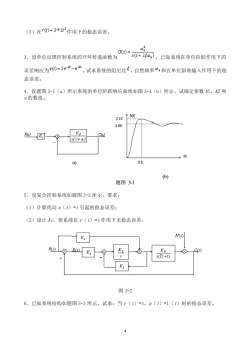
4 （3）在 作用下的稳态误差。 3．设单位反馈控制系统的开环传递函数为 ，已知系统在单位阶跃作用下的 误差响应为 。试求系统的阻尼比 ，自然频率 和在单位斜坡输入作用下的稳 态误差。 4．设题图 3-1（a）所示系统的单位阶跃响应曲线如图 3-1（b）所示，试确定参数 K1、K2 和 a 的数值。 (b) 题图 3-1 5．设复合控制系统如题图 3-2 所示，要求： （1）计算扰动 n（t）=t 引起的稳态误差； （2）设计 Kc，使系统在 r（t）=t 作用下无稳态误差。 图 3-2 6．已知系统结构如题图 3-3 所示，试求：当 r（t）=t，n（t）=1（t）时的稳态误差

+1 1 CO 图3-3 7.设单位反馈系统的开环传递函数为 G(5)=s(0.1s+1) 500 当下列输入时，求其稳态误差 )0= 2 (2)x,(0=1+21+21 8.某单位反馈系统，其开环传递函数为 10 GS)=s0.1s+) (1)试求静态误差系数k。,k,k。 （2)当输入为x0=a,+a1+受时，试求系统的稳态误差。 9.如图3一4所示系统，当x,()=10+21时，试求系统的稳态误差： 当x,()=s(6)时，试求稳态时误差的幅值。 图3-4 10.某系统的方块图如图3一5所示

5 图 3-3 7．设单位反馈系统的开环传递函数为 (0.1 1) 500 ( ) + = s s G S 当下列输入时，求其稳态误差 （1） 2 ( ) 2 t x t i = （2） 2 x (t) 1 2t 2t i = + + 8．某单位反馈系统，其开环传递函数为 (0.1 1) 10 ( ) + = s s G S （1）试求静态误差系数 p v a k , k , k （2）当输入为 2 2 0 1 2 ( ) t a xi t = a + a t + 时，试求系统的稳态误差。 9．如图 3－4 所示系统，当 x t t i ( ) = 10 + 2 时，试求系统的稳态误差； 当 x (t) sin( 6t) i = 时，试求稳态时误差的幅值。 10．某系统的方块图如图 3－5 所示。 图 3-4

(1)当输入x,()=101时，试求其稳态误差： 图3-5 (2)当输入x,)=4+61+32时，试求其稳态误差； 第四章 1.设控制系统的开环传递函数为 G(s)H(s)= K s(1+Ts)(1+Ts) ·试分析不同K值时系统的稳定性 ·确定当了=1,3=0,5和K=0.75时系统的幅值裕量。 2.最小相角系统对数幅频渐进特性如题图4-1所示，请确定系统的传递函数。 木L(o1dB 300 0 0 20 0.1 四 题图4-1 3.系统结构图如题图4-2所示，试用奈魁斯特判据判别其稳定性。 200 10 s 1025+1万 2s 图4-2 4.设单位反馈控制系统的开环传递函数为 6

6 （1）当输入 x t t i ( ) = 10 时，试求其稳态误差； （2）当输入 2 x (t) 4 6t 3t i = + + 时，试求其稳态误差； 第四章 1．设控制系统的开环传递函数为 • 试分析不同 K 值时系统的稳定性; • 确定当 , 0.75 时系统的幅值裕量。 2.最小相角系统对数幅频渐进特性如题图 4-1 所示，请确定系统的传递函数。 题图 4-1 3．系统结构图如题图 4-2 所示，试用奈魁斯特判据判别其稳定性。 图 4-2 4．设单位反馈控制系统的开环传递函数为 图 3-5

c6)s0+01s0+02s0+月 ,绘制K=1时系统的伯德图： ·确定使系统在闭环时处于临界稳定的速度误差系数： ·确定幅值裕量为10分贝时的速度误差系数及相应的相角裕量。 5.画出下列传递函数的伯德图 (1)G(S)= 20 0.5s+10.1s+1) (2)GS9=0.4s+1X0.04s+0 2s2 (3)GS=500.6s+D s2(4s+1) (4)GS)=750.2s+16+D s(s2+165+100) 6.某单位反馈系统的开环传递函数 试求以下列输入时输出x。的稳态响应表达式。 (1)x,(d)=simt+30) (2)x,(0-2c0s21-45) 7.某单位反馈系统的开环传递函数 G(5)-3(s+D)

7 • 绘制 时系统的伯德图； • 确定使系统在闭环时处于临界稳定的速度误差系数； • 确定幅值裕量为 10 分贝时的速度误差系数及相应的相角裕量。 5．画出下列传递函数的伯德图 （1） (0.5 1)(0.1 1) 20 ( ) + + = s s s G S （2） (0.4 1)(0.04 1) 2 ( ) 2 + + = s s s G S （3） (4 1) 50(0.6 1) ( ) 2 + + = s s s G S （4） ( 16 100) 7.5(0.2 1)( 1) ( ) 2 + + + + = s s s s s G S 6．某单位反馈系统的开环传递函数 1 10 ( ) + = s G S 试求以下列输入时输出 o x 的稳态响应表达式。 （1） ( ) sin( 30 )  xi t = t + （2） ( ) 2cos(2 45 )  xi t = t − 7．某单位反馈系统的开环传递函数 2 ( 1) 1 ( ) + = s s G S

试求其剪切频率)，并求出频率对应的相角 8.试求出下列系统的乃氏图 (1)GS)=s+1X2s+) 1 (2)G(S)=35+1X2s+0 1 (0.2s+100.025s+1) (3)GS)=005s+1X0001s+D 第五章 1.设G(S)= 5-)HS)=1+K,试确定闭环系统稳定时的K,的临界值。 10 2.对于下列系统，试画出其伯德图，求出相角裕量y和增益裕量，并判其稳定性。 250 (1)G(S)H(S)= s0.03s+10.0047s+1) 250(0.5s+1) (2)G(SHS)=00s+1X003s+1X00047s+D 3.设单位反馈系统的开环传递函数为 10K(s+0.5) G(SH(S)= s2(s+2(s+10) 试用乃氏判据确定系统在K=1和K=10时的稳定性。 4.设单位反馈系统的开环传递函数为 G(S)H(S)= (s+1(s+2)

8 试求其剪切频率 c ，并求出频率对应的相角 8．试求出下列系统的乃氏图 （1） ( 1)(2 1) 1 ( ) + + = s s G S （2） ( 1)(2 1) 1 ( ) 2 + + = s s s G S （3） (0.005 1)(0.001 1) (0.2 1)(0.025 1) ( ) 2 + + + + = s s s s s G S 第五章 1．设 ( 1) 10 ( ) − = s s G S , H S K s =1+ n ( ) ，试确定闭环系统稳定时的 Kn 的临界值。 2．对于下列系统，试画出其伯德图，求出相角裕量  和增益裕量，并判其稳定性。 （1） (0.03 1)(0.0047 1) 250 ( ) ( ) + + = s s s G S H S （2） (10 1)(0.03 1)(0.0047 1) 250(0.5 1) ( ) ( ) + + + + = s s s s s G S H S 3.设单位反馈系统的开环传递函数为 ( 2)( 10) 10 ( 0.5) ( ) ( ) 2 + + + = s s s K s G S H S 试用乃氏判据确定系统在 K=1 和 K=10 时的稳定性。 4.设单位反馈系统的开环传递函数为 ( 1)( 2) ( ) ( ) + + = s s s K G S H S

试确定使系统稳定的K值范围。 5.试判断下列系统的稳定性 10 (1)G(S)H(S)= s(-1)(s+5) (2)GS)H(S)= 10(s+1) s(s-1)(2s+3) 第六章 1.某系统的开环传递函数G,(S)= 360(0.1s+1) 要求近似保持上述系统的过渡过 s(0.9s+1)0.007s+1)(0.005s+1) 程时间和稳定裕度不变，使它的速度误差等于，【， ，试设计校正环节。 1000 2.设单位反馈系统的开环传递函数为 40 G(s)= s(0.2s+1)(0.0625s+1) 要求校正后系统的相角裕度为50°，幅值裕度在30-50B,试设计串联校正装置。 3.设单位反馈系统的开环传递函数 K G(s)= s(s+1)(0.25s+1) 若要求校正后系统的静态速度误差系数K,≥5 rad/s,相角裕度为Y≥45°，试设计校正装置。 4.某单位反馈系统的开环传递函数G,(S)=。K ，欲使系统开环放大倍数K=20s1,相位裕度不 s(0.5s+1) 小于50°，幅值裕度不小于10B,试求系统的校正装置。 K 4.某单位反馈系统的开环传递函数G(S)= ,欲使K,=5,相位裕度不小于40°，幅值裕 s(s+1)0.5s+1) 度不小于10dB,试求系统的校正装置。 9

9 试确定使系统稳定的 K 值范围。 5．试判断下列系统的稳定性 （1） ( 1)( 5) 10 ( ) ( ) − + = s s s G S H S （2） ( 1)(2 3) 10( 1) ( ) ( ) − + + = s s s s G S H S 第六章 1．某系统的开环传递函数 (0.9 1)(0.007 1)(0.005 1) 360(0.1 1) ( ) 0 + + + + = s s s s s G S ，要求近似保持上述系统的过渡过 程时间和稳定裕度不变，使它的速度误差等于 1000 1 ，试设计校正环节。 2．设单位反馈系统的开环传递函数为 要求校正后系统的相角裕度为 ,幅值裕度在 30-50dB,试设计串联校正装置。 3．设单位反馈系统的开环传递函数 若要求校正后系统的静态速度误差系数 ，相角裕度为 ，试设计校正装置。 4．某单位反馈系统的开环传递函数 (0.5 1) ( ) 0 + = s s K G S ，欲使系统开环放大倍数 1 20 − K = s ,相位裕度不 小于  50 ,幅值裕度不小于 10dB，试求系统的校正装置。 4．某单位反馈系统的开环传递函数 ( 1)(0.5 1) ( ) 0 + + = s s s K G S ，欲使 Kv = 5,相位裕度不小于  40 ,幅值裕 度不小于 10dB，试求系统的校正装置