《机械工程控制基础》课程教学资源（讲稿）第六章 系统的性能与校正

第六章系统的性能与校正 讲授内容 6.1系统的性能指标 系统性能指标，按其类型可分为： (1)时域性能指标，它包括瞬态性能指标和稳态性能指标。其 中，瞬态性能指标一般是在单位阶跃输入下，由输出的过渡过程 所给出的，实质上是由瞬态响应所决定的，它主要包括延迟时间 14、上升时间1，、峰值时间1。、最大超调量或最大百分比超调量M 及调整时间（或过渡过程时间)·，等稳态性能指标主要指稳态 误差。 (2)频域性能指标，主要包括相位裕度y、幅值裕度K,、复 现频率0m、复现带宽0~0m、截止频率o,和截止带宽0~0等。 必须注意，系统频域性能指标与时域性能指标间存在一定的 关系，如峰值时间1，和调整时间1，都与系统的带宽有关：系统的 带宽越大，则系统响应的快速性就越好。 (3)综合性能指标（误差准则）是系统性能的综合测度。它们 是系统误差0)的某个函数的积分。在系统参数取最优值时，这 些指标将取极值，从而可以通过选择适当的参数得到综合性能指 标最优的系统。主要有以下三种： (a)误差积分性能指标：I=()d,适用于无超调系统。 (b)误差平方积分性能指标：1=e(u)d,适用于有超调系 统，其特点是，重视大的误差，忽略小的误差。根据这个指标设

第六章 系统的性能与校正 讲授内容 6.1 系统的性能指标 系统性能指标，按其类型可分为： (1)时域性能指标,它包括瞬态性能指标和稳态性能指标。其 中 ,瞬态性能指标一般是在单 位阶跃输入下,由输出的过渡过程 所给出的,实质上是由瞬态响应所决 定的,它主要包括延迟时间 、上升时间 、峰值时间 、最大超调量或最大百分比超调量 及调整时间 （或过渡过程时间） 等 ； 稳态性能指标主要指稳态 误差。 d t r t p t M p s t ( 2 )频域性能指标，主要包括相位裕度 γ 、幅值裕度 、 复 现频率 K g ω m、复现带宽 0 ~ω m、截止频率 ω b 和截止带宽 0 ~ω b 等。 必须注意，系统频域性能指标与时域性能指标间存在一定的 关系，如峰值时间 和调整时间 都与系统的带宽有关：系统的 带宽越大，则系统响应的快速性就越好。 p t s t (3)综合性能指标(误差准则)是系统性能的综合测度。它们 是系统误差 的某个函数的积分。在系统参数取最优值时，这 些指标将取极值，从而可以通过选择适当的参数得到综合性能指 标最优的系统。主要有以下三种: e(t) (a)误差积分性能指标： ，适用于无超调系统。 ∫ ∞ = 0 I e(t)dt ( b )误差平方积分性能指标： ，适用于有超调系 统 ，其特点是，重视大的误差，忽略小的误差。根据这个指标设 ∫ ∞ = 0 2 I e (t )dt

计的系统，能使大的误差迅速减小，但系统容易产生振荡。 (c)广义误差平方积分性能指标：1=[e2)+ae2()d,其特 点是不容许大的动态误差和大的误差变化率长期存在。根据这个 指标设计的系统，过渡过程结束快，而且其变化也比较平稳。 6.2系统的校正 一、校正的概念 所谓的校正（或称补偿），就是指在系统中增加新的环节， 以改善系统性能的方法。 二、校正的分类 校正方案：确定所采用的校正环节及其在系统中的位置，两 者合称为校正方案。线性定常系统的常用校正方案有： 增益调整 相位超前校正 串联校正 相位想潘后等收正 PD调节 并联校正 反馈校正 顺馈校正 6.3无源校正 串联校正可以分为无源校正和有源校正，其中无源校正包括 增益调整、相位超前校正、相位滞后校正以及相位滞后一一超前 校正等四种方式。由于单纯采用增益调整，不能同时保证系统的 稳定性和系统稳态精度都得到改善，往往在提高系统的稳定性的 同时，降低了系统响应的准确性，或者相反。因此，一般不采用 单纯的增益调整

计的系统，能使大的误差迅速减小，但系统容易产生振荡。 (c)广义误差平方积分性能指标： ，其 特 点是不容许大的动态误差和大的误差变化率长期存在。根据这个 指标设计的系统，过渡过程结束快，而且其变化也比较平稳。 ∫ ∞ = + 0 2 2 I [ e (t ) αe& (t )]dt 6.2 系统的校正 一、校正的概念 所谓的校正（或称补偿），就是指在系统中增加新的环 节 ， 以改善系统性能的方法。 二、校正的分类 校正方案： 确定所采用的校正环节及其在系统中的位置， 两 者合称为校正方案。线性定常系统的常用校正方案有： ⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ 顺馈校正 反馈 正 并联校正 调节 相位超前 滞后校正 相位滞后校正 相位超前校正 增益调整 串联校正 校 PID — — 6.3 无源校正 串联校正可以分为无源校正和有源校正，其中无源校正包括 增益调整、相位超前校正、相位滞后校正以及相位滞后——超前 校正等四种方式。由于单纯采用增益调整，不能同时保证系统的 稳定性和系统稳态精度都得到改善，往往在提高系统的稳定性的 同时，降低了系统响应的准确性，或者相反。因此，一般不采用 单纯的增益调整

一、相位超前校正 1.相位超前校正环节 相位超前环节的传递函数可用下式表示 G) (6.3.1) 式中，a0. 可见相位超前。它的幅频特性为： K.Vo)-aMToy+i (aTo)2+1 将G(Uo)分为实部u和虚部v,可得 Q+a) 图6.3.1 可见，G.Uo)的Nyquist轨迹是一个过点(1，j0),半径为1-)， 圆心为片1+a,j0的半圆。又由于相角∠G。Uo)是正的，故G.o)轨 迹是其中的上半圆，如图6.3.1所示。 若此环节的最大相位超前角为p,则由 (6.3.2) 可知，当α减小时，p增大，如图63.2所示。从图中还可以看 出，随着频率o的减小，幅值G(@减小，所以，超前环节相当 于高通滤波器。 图6.3.3是相位超前环节Go=am+出的B0de图。其中频 (ja@+1

一、相位超前校正 1．相位超前校正环节 相位超前环节的传递函数可用下式表示 ( 1) ( 1) ( ) + + = Ts Ts G s c α α ， （ 6.3.1） 式中， α 0。 可见相位超前。它的幅频特性为： ( ) 1 ( ) 1 ( ) 2 2 + + = α ω ω ω α T T G j c 将 G ( jω) c 分为实部 u 和虚部 v ，可得 2 2 2 2 1 2 1 ( u ) v ( ) α −α + = + − , 图 6.3.1 可 见 ，Gc ( jω) 的 Nyquist 轨迹是一个过点（ 1,j0）,半径为 (1 ) 2 1 −α ， 圆心为 (1 ), 0] 2 1 [ +α j 的半圆。又由于相角 G ( jω) ∠ c 是正的，故 G ( jω) c 轨 迹是其中的上半圆，如图 6.3.1 所示。 若此环节的最大相位超前角为 ϕ m ，则由 α α ϕ + − = 1 1 sin m （ 6.3.2） 可知，当 α 减小时， ϕ m 增大，如图 6.3.2 所示。从图中还可以看 出 ， 随着频率 ω 的减小， 幅 值 G ( jω) c 减小， 所以， 超前环节相当 于高通滤波器。 图 6.3.3 是相位超前环节 ( j T ) ( jT ) G ( j ) c 1 1 + + = α ω ω ω α 的 Bode 图。其中频

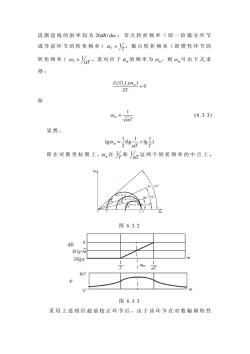
段渐进线的斜率均为20dB/dec;零点转折频率（即一阶微分环节 或导前环节的转角频率)，=人：极点转折频率（即惯性环节的 转角频率)，=么7·设对应于的频率为日，则a可由下式求 得： OLG.(jo)=0 OT 即 o.-JaT (6.3.3) 显然， go,=g7+lg宁 即在对数坐标图上，在和这两个转折频率的中点上。 m 图6.3.2 dB 0 201ga 90 图6.3.3 采用上述相位超前校正环节后，由于该环节在对数幅频特性

段渐进线的斜率均为 ；零点转折频率（即一阶微分环节 或导前环节的转角频率） 20dB / dec T T ω = 1 ；极点转折频率（即惯性环节的 转角频率） T αT ω = 1 。设对应于 ϕ m 的频率为 ω m，则 ω m可由下式求 得 ： 0 ( ) = ∂ ∂∠ T G j c ω m 即 T m α ω 1 = ( 6.3.3) 显然， ) 1 lg 1 (lg 2 1 lg T T m = + α ω 即在对数坐标图上，ω m在 T 1 和 αT 1 这两个转折频率的中点上。 图 6.3.2 图 6.3.3 采用上述相位超前校正环节后，由于该环节在对数幅频特性

上有20dB/dec段存在，故加大了系统的剪切频率o。、谐振频率o,与 截止频率，其结果是加大了系统的带宽，加快了系统的响应速 度：又由于相位超前，还可能加大相位裕度，其结果是增加了系 统的相对稳定性。 2.采用Bode图进行相位超前校正 采用相位超前校正的一般设计步骤为： (1)根据系统稳态误差的要求，确定系统的开环增益K: (2)在已确定K值的条件下，计算未校正系统的相位裕度： (3)根据指标的要求，确定在系统中需要增加的相角超前量 Put (4)由式(6.3.2)确定α值，然后根据式(6.3.3)确定最大 超前角对应的频率o处的对数幅频特性值L.,即 L.=20g1+T@ 1+j。在未校正系统的对数幅频特好 1+jaTo -20lg+j小a 上找到幅值等于-L.点所对应的频率，该频率即为校正后系统新 的剪切频率⊙，同时也是所选超前网络的o,在此频率上超前网 络将产生最大超前相角值m；根据om确定T和aT: (5)确定超前校正环节的转折频率on=片，on=片a) (6)验算。 3.相位超前校正的特点 (1)相位超前校正主要对未校正系统在中频段的特性进行校 正。以确保校正后系统具有较高的相位裕度及中频段斜率等于 -20dB/dec。 (2)超前校正可以提高系统响应的快速性。相位超前校正环 节校正使系统截止频率增大，提高系统的响应速度。但随着带宽

上 有 20dB / dec 段存在，故加大了系统的剪切频率 ωc、谐振频率 ω r 与 截止频率 ωb ，其结果是加大了系统的带宽，加快了系统的响应速 度 ；又由于相位超前，还可能加大相位裕度，其结果是增加了系 统的相对稳定性。 2．采用 Bode 图进行相位超前校正 采用相位超前校正的一般设计步骤为： (1)根据系统稳态误差的要求，确定系统的开环增益 K ； (2)在已确定 K 值的条件下，计算未校正系统的相位裕度； (3)根据指标的要求，确定在系统中 需要增加的相角超前量 ϕ m ； (4)由式（ 6.3.2）确定 α 值，然后根据式（ 6.3.3）确定最大 超前角对应的频率 ω m 处的对数幅频特性值 Lm , 即 j a a j lg jaT jT L lg m m m + + = + + = 1 1 1 20 1 1 20 ω ω 。 在未校正系统的对数幅频特性图 上找到幅值等于 点所对应的频率，该频率即为校正后系统新 的剪切频率 − Lm ωc ′，同时也是所选超前网络的 ω m，在此频率上超前网 络将产生最大超前相角值 ϕ m ；根据 ω m，确定 T 和 αT ； (5)确定超前校正环节的转折频率 T T 1 ω 1 = ， ( T ) T α ω 1 2 = ； (6)验算。 3．相位超前校正的特点 (1)相位超前校正主要对未校正系统 在中频段的特性进行校 正。以确保校正后系统具有较高的 相位裕度及中频段斜率等于 − 20dB / dec 。 (2)超前校正可以提高系统响应的快 速性。相位超前校正环 节校正使系统截止频率增大，提高系统的响应速度。但随着带宽

的增大，系统抗干扰能力下降。 (3)由于系统的增益和型次都未变化，因此对系统的稳态精 度无明显改善。 (4)相位超前校正的适用范围有限制。如果在未校正系统的 截止频率附近，相频特性的变化率很大，即相角减小得很快，则 采用单级相位超前校正的效果将不大。这是因为随着校正后的截 止频率向高频段的移动，相角在附近将减小得很快，于是在新的 截止频率上便很难得到足够大的相位裕度。 二、相位滞后校正 1.相位滞后校正环节 相位滞后校正环节可用下式表示： G.s)=+1 BTs+1 式中，B>1,T为常数。 此相位滞后环节的频率特性为G.(o)=+m@ 1+T0 (B>1) 其中，相频特性为 ZG(j@)=arctanTo arctan BT@<0 可见相位滞后。它的幅频特性为 .(Jo)-/(ToY+1 (BTo)+1 将G(Uo)分为实部u和虚部v,可求得 u-+r= 2B1 26

的增大，系统抗干扰能力下降。 (3)由于系统的增益和型次都未变化 ，因此对系统的稳态精 度无明显改善。 (4)相位超前校正的适用范围有限制 。如果在未校正系统的 截止频率附近，相频特性的变化率很大，即相角减小得很快，则 采用单级相位超前校正的效果将不大。这是因为随着校正后的截 止频率向高频段的移动，相角在附近将减小得很快，于是在新的 截止频率上便很难得到足够大的相位裕度。 二、相位滞后校正 1．相位滞后校正环节 相位滞后校正环节可用下式表示： 1 1 + + = Ts Ts G (s) c β ， 式中， β > 1， T 为常数。 此相位滞后环节的频率特性为 β ω ω ω j T jT G j c + + = 1 1 ( ) (β > 1) 其中，相频特性为 ∠Gc ( jω) = arctanTω − arctan βTω < 0 可见相位滞后。它的幅频特性为 ( ) 1 ( ) 1 ( ) 2 2 + + = β ω ω ω T T G j c 将 G ( jω) c 分为实部 u 和虚部 v ，可求得 2 2 2 ) 2 1 ) ( 2 1 ( β β β β − + = + u − v

21+) 图6.3.4 可见，G.Uo)的Nyquist轨迹是一个过点(1j0),半径为0-合 圆心为+分0的半圆。又由于相角∠6.Uo)是负的，故G.Uo) 的Nyquist轨迹是下半圆，如图6.3.4所示。 若此环节的最大相位滞后角为？。，则 m.月别 图6.3.5是相位滞后环节的Bode图。其对数幅频特性中频段 的渐近线为直线，斜率为-20dB/dcc；零点转折频率a,=片：极 点转折频率a,=片m)设对应于0的频率为0，则0. 位于光m)和片的中点上。 由图6.3.4和6.3.5可知，滞后校正环节是一个低通环节，具 有很强的高频衰减作用。该环节校正的原理是：当增加系统的开 环增益时，其幅频特性曲线上移，而相频特性曲线则不变。此时， 如果保证片远远小于增益交接频率0。，则在0.附近系统开环增 益大大降低，而相位变化不大，这样，校正后系统的增益交接频 率。小于®，相位交接频率基本不变。又由于一般系统校正前 的开环相频特性在增益交接频率。附近是下降的，于是，系统的

图 6.3.4 可 见 ，G ( jω) c 的 Nyquist 轨迹是一个过点（ 1,j0）,半径为 ) 1 (1 2 1 β − ， 圆心为 ), 0] 1 (1 2 1 [ j β + 的半圆。 又由于相角 G ( jω) ∠ c 是负的， 故 G ( jω) c 的 Nyquist 轨迹是下半圆，如图 6.3.4 所示。 若此环节的最大相位滞后角为 ϕ m ， 则 1 1 sin + − = β β ϕ m 图 6.3.5 是相位滞后环节的 Bode 图 。其对数幅频特性中频段 的渐近线为直线，斜率为 − 20dB / dec ；零点转折频率 T T ω = 1 ； 极 点转折频率 ( T ) T β ω = 1 。设对应于 ϕ m 的频率为 ω m， 则 T m β ω 1 = ， 位 于 ( βT ) 1 和 T 1 的中点上。 由 图 6.3.4 和 6.3.5 可 知 ,滞后校正环节是一个低通环节，具 有很强的高频衰减作用。该环节校正的原理是：当增加系统的开 环增益时，其幅频特性曲线上移，而相频特性曲线则不变。此时， 如果保证 T 1 远远小于增益交接频率 ωc ，则在 ωc 附近系统开环增 益大大降低，而相位变化不大，这样，校正后系统的增益交接频 率 c ω' 小 于 ωc ，相位交接频率基本不变。又由于一般系统校正前 的开环相频特性在增益交接频率 ωc 附近是下降的，于是，系统的

相位裕度增加。同时，校正环节的高频衰减作用，还使得系统的 幅值裕度有所增加。因此，相位滞后校正环节的校正作用在于其 高频衰减作用，而不是相位滞后作用。 dB -201gB -90 图6.3.5 2.采用Bode图进行相位滞后校正 如上所述，相位滞后校正主要利用滞后校正环节的高频幅值 衰减特性，使截止频率下降，即<®。，从而使系统获得足够的 相位裕度。因此，应尽可能使其最大相角滞后处在较低频段内。 相位滞后校正适用于系统响应速度要求不高而滤波噪声性能要 求较高的情况。此外，如果未校正系统具有满意的动态特性，而 其稳态性能指标不满足要求时，也可以采用相位滞后校正来提高 其稳态精度，同时保持其动态性能基本不变 采用相位滞后校正的一般设计步骤为： ()根据系统稳态误差的要求，确定系统的开环增益K: (2)作Gx(Uo)的Bode图，找出未校正系统的相位裕度和幅值 裕度： (3)在GxUo)的Bode图上，找出相位裕度为y+(5°~12)的频 率点，并选这点为已校正系统的剪切频率。此处y为要求的相位 裕度： (4)相位滞后校正环节的零点转折频率选为低于已校正系统 的剪切频率的5-10倍： (5)在Gx(Uo)的Bode图上，在已校正系统的剪切频率点上

相位裕度增加。同时，校正环节的高频衰减作用，还使得系统的 幅值裕度有所增加。因此，相位滞后校正环节的校正作用在于其 高频衰减作用，而不是相位滞后作用。 图 6.3.5 2．采用 Bode 图进行相位滞后校正 如上所述，相位滞后校正主要利用滞后校正环节的高频幅值 衰减特性， 使截止频率下降， 即 ωc < ωc ′ ， 从而使系统获得足够的 相位裕度。因此，应尽可能使其最大相角滞后处在较低频段内。 相位滞后校正适用于系统响应速度 要求不高而滤波噪声性能要 求较高的情况。此外，如果未校正系统具有满意的动态特性，而 其稳态性能指标不满足要求时，也可以采用相位滞后校正来提高 其稳态精度，同时保持其动态性能基本不变。 采用相位滞后校正的一般设计步骤为： (1)根据系统稳态误差的要求，确定系统的开环增益 K； (2)作 G ( jω) K 的 Bode 图，找出未校正系统的相位裕度和幅值 裕度； (3)在 G ( jω) K 的 Bode 图上，找出相位裕度为 γ + (5° ~ 12°) 的 频 率点，并选这点为已校正系统的剪切频率。此处 γ 为要求的相位 裕度； (4)相位滞后校正环节的零点转折频 率选为低于已校正系统 的剪切频率的 5~10 倍 ； (5)在 G ( jω) K 的 Bode 图上，在已校正系统的剪切频率点上

找到使Gxo)的对数幅频特性下降到0分贝所需的衰减分贝值， 而此值为-20gB，从而确定滞后校正环节的极点转折频率 a=光Bm) (6)验算。 3.相位滞后校正的特点 ()由于相位滞后校正的作用主要在于提高系统的开环放大 系数，从而改善系统的稳态性能，而对系统原有的动态性能不呈 显著的影响。因此，主要用于未校正系统的动态性能尚能满足性 能指标的要求，而只需要增加开环增益以提高系统控制精度的 些系统中。 (2)滞后校正环节本质上是一种低通滤波器。因此，经滞后 校正后的系统对低频段信号具有较高的放大能力，这样便可降低 系统的稳态误差；但对高频段的信号，系统却表现出显著的衰减 特性。这样就有可能在系统中防止不稳定现象的出现。应特别注 意，对于相位滞后校正是利用它对高频信号的锐减特性，而不是 利用其相角滞后的特性。因此，应加在原系统的低频段。 (3)相位滞后校正降低了系统的响应的快速性。由于采用了 相位滞后校正环节校正使系统带宽变窄，这说明了滞后校正在提 高系统的动态过程平稳性方面有较好的效果，系统抗干扰能力增 强，但系统的响应速度降低。 三、相位滞后一超前校正 1.相位滞后一超前环节 相位滞后一超前环节可用下式表示 G.(o)=（s+T,s+1) (分5+Xm,s+D 式中，B>1,T,I2为常数

找到使 G ( jω) K 的对数幅频特性下降到 0 分贝所需的衰减分贝值， 而此值为 − 20lg β ，从而确定滞后校正环节的极点转折频率 ( T ) T β ω 1 1 = ； (6)验算。 3．相位滞后校正的特点 (1)由于相位滞后校正的作用主要在 于提高系统的开环放大 系数，从而改善系统的稳态性能，而对系统原有的动态性能不呈 显著的影响。因此，主要用于未校正系统的动态性能尙能满足性 能指标的要求，而只需要增加开环增益以提高系统控制精度的一 些系统中。 (2)滞后校正环节本质上是一种低通 滤波器。因此，经滞后 校正后的系统对低频段信号具有较高的放大能力，这样便可降低 系统的稳态误差；但对高频段的信号，系统却表现出显著的衰减 特性。这样就有可能在系统中防止不稳定现象的出现。应特别注 意 ，对于相位滞后校正是利用它对高频信号的锐减特性，而不是 利用其相角滞后的特性。因此，应加在原系统的低频段。 (3)相位滞后校正降低了系统的响应 的快速性。由于采用了 相位滞后校正环节校正使系统带宽变窄，这说明了滞后校正在提 高系统的动态过程平稳性方面有较好的效果，系统抗干扰能力增 强，但系统的响应速度降低。 三、相位滞后—超前校正 1．相位滞后—超前环节 相位滞后—超前环节可用下式表示 1)( 1) 1 ( ( 1)( 1) ( ) 1 2 1 2 + + + + = T s T s T s T s G s c β β 式中， β > 1， T1 ,T2为常数

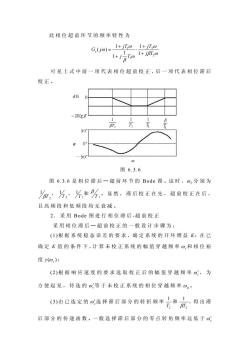
此相位超前环节的频率特性为 G.Uo)=1+I.1+ 1+J分o1+ma 可见上式中前一项代表相位超前校正，后一项代表相位滞后 校正。 dB -20g8 90 0 -909 图6.3.6 图6.3.6是相位滞后一超前环节的Bode图。这时，o,分别为 m,片片和片·显然，滞后校正在先，超前校正在后， 且高频段和低频段均无衰减。 2.采用Bode图进行相位滞后-超前校正 采用相位滞后一超前校正的一般设计步骤为： (1)根据系统稳态误差的要求，确定系统的开环增益K:在已 确定K值的条件下，计算未校正系统的幅值穿越频率0。和相位裕 度y(o): (2)根据响应速度的要求选取校正后的幅值穿越频率⊙：，为 方便起见，待选的等于未校正系统的相位穿越频率®g· ()油已定的选择指后都分的转折频率和，得出 后部分的传递函数。一般选择滞后部分的零点转角频率远低于

此相位超前环节的频率特性为 β ω ω ω β ω ω 2 2 1 1 1 1 1 1 1 ( ) j T jT j T jT G j c + + ⋅ + + = 可见上式中前一项代表相位超前校正，后一项代表相位滞后 校正。 图 6.3.6 图 6.3.6 是相位滞后—超前环节的 Bode 图 。这时，ωT 分别为 2 1 βT ， 2 1 T ， 1 1 T 和 T 1 β 。显然，滞后校正在先，超前校正在后， 且高频段和低频段均无衰减。 2．采用 Bode 图进行相位滞后 -超前校正 采用相位滞后—超前校正的一般设计步骤为： (1)根据系统稳态误差的要求，确定系统的开环增益 K；在 已 确 定 K 值的条件下，计算未校正系统的幅值穿越频率 ωc和相位裕 度 ( ) ωc γ ； (2)根据响应速度的要求选取校正后的幅值穿越频率 ωc ′， 为 方便起见，待选的 ωc ′等于未校正系统的相位穿越频率 ω g 。 (3)由已选定的 ωc ′选择滞后部分的转折频率 2 1 T 和 2 1 βT ，得出滞 后部分的传递函数。一般选择滞后部分的零点转角频率远低于 ωc ′