《电路理论》课程教学课件(讲稿)第9章 正弦稳态电路的分析
第9章正弦稳态电路的分析 本章重点 9.1 阻抗和导纳 9.3 正弦稳态电路的分析 9.4 正弦稳态电路的功率 9.5 复功率 9.6 最大功率传输 首页
第9章 正弦稳态电路的分析 首 页 本章重点 9.3 正弦稳态电路的分析 9.4 正弦稳态电路的功率 9.5 复功率 9.6 最大功率传输 9.1 阻抗和导纳

●重点: 1.阻抗和导纳; 2.正弦稳态电路的分析; 3.正弦稳态电路的功率分析:
2. 正弦稳态电路的分析; 3. 正弦稳态电路的功率分析; 重点: 1. 阻抗和导纳; 返 回
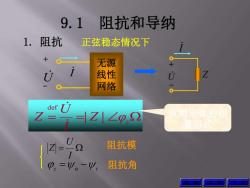
9.1 阻抗和导纳 1.阻抗 正弦稳态情况下 无源 线性 网络 f U Z= Z|∠p.2 欧姆定律的相 量珍式 U 14-78 阻抗模 阻抗角 回
9.1 阻抗和导纳 1. 阻抗 正弦稳态情况下 I U Z + - 无源 线性 网络 I U + - Z φz I U Z | | def z u i I U Z 阻抗模 阻抗角 欧姆定律的相 量形式 返 回 上 页 下 页
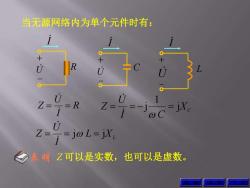
当无源网络内为单个元件时有: U Z= .-R Z= Z==j0L-iX, 表明Z可以是实数, 也可以是虚数
当无源网络内为单个元件时有: R I U Z L XL I U Z j j X C I C U Z j 1 j Z 可以是实数,也可以是虚数。 I C U + - 上 页 下 页 I U R + - I L U + - 表明 返 回
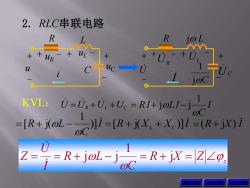
2.RLC串联电路 R R 10L AVAA ++uR -+U u I joc KVL: U-Ux+U.+Uc-Ri+joLi-j =R+aLoCi=R+jX+X-]/=R+o/ U Z-5-R+jol-joc-R+ix-12o
2. RLC串联电路 KVL: . . . . . . . 1 j j I C U UR UL UC RI LI I R X X I C R L L C )] [ j( )] 1 [ j( R X I ( j ) R X Z z C R L I U Z j 1 j j 上 页 下 页 L C R u uL uC i + - + - + - + - uR R + - + - + - + - . I j L U UL U C . jC 1 UR 返 回

Z一复阻抗;☑一复阻抗的模;p2一 阻抗角; R一电阻(阻抗的实部);X一电抗(阻抗的虚部)。 转换关系: .=arctan R R=☑cos0: U 或 X=Zsing. p.=Ψ。-Ψ 阻抗三角形
Z — 复阻抗;|Z| —复阻抗的模;z —阻抗角; R —电阻(阻抗的实部);X—电抗(阻抗的虚部)。 转换关系: arctan | | 2 2 R X φ Z R X z 或 R=|Z|cosz X=|Z|sinz 阻抗三角形 |Z| R X z z u i I U Z 返 回 上 页 下 页
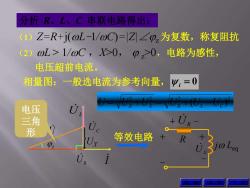
分析R、L、C串联电路得出 (1) Z=R+j(oL-1/oC=Z∠p,为复数,称复阻抗 (2) oL>1/oC,0,p,>0,电路为感性, 电压超前电流。 相量图:一般选电流为参考向量, 4,=0 电压 U 三角 形 Ux 等效电路
I 分析 R、L、C 串联电路得出: (1)Z=R+j(L-1/C)=|Z|∠z 为复数,称复阻抗 (2)L > 1/C ,X>0, z>0,电路为感性, 电压超前电流。 i 0 上 页 下 页 相量图:一般选电流为参考向量, UC UR UL U z UX 电压 三角 形 2 L C 2 2 2 U U U U (U U ) R X R j Leq UX + R - + - + UR - 等效电路 返 回
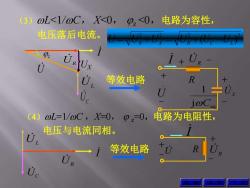
(3) oL<1/oC,X<0,p,<0,电路为容性, 电压落后电流。 U 等效电路 R j@Ce (4)oL=1/o0C,X=0,p,=0,电路为电阻性, 电压与电流同相。 等效电路
I (3)L<1/C, X<0, z <0,电路为容性, 电压落后电流。 UC UR UL U z UX 等效电路 上 页 下 页 UX eq j 1 C R + - + - + UR - . U I (4)L=1/C ,X=0, z=0,电路为电阻性, 电压与电流同相。 I UR UL UC R + - + - I UR 等效电路 U 2 2 2 2 ( ) U UR UX UR UC UL 返 回

例 已知:R=152,L-0.3mH,C=0.2uF, u=5V2cos(o+60),f=3×10Hz. 求i,4g,山,C: R 1o! 解 画出相量模型 U=5∠60°V j0L=j2π×3×104×0.3×103 =j56.52 2元×3×104×0.2×106 =-j26.50 Rjow ,=15+j56.5-j26.5 =33.54∠63.4°2 回
例 已知:R=15, L=0.3mH, C=0.2F, 5 2cos( 60 ), 3 10 Hz . 4 u t f 求 i, uR , uL , uC . 解 画出相量模型 5 60 V U C Z R L 1 j j j56.5Ω j j2π 3 10 0.3 10 4 3 L j26.5Ω 2π 3 10 0.2 10 1 j 1 j 4 6 C 15 j56.5 j26.5 33.54 63.4 Ω o 上 页 下 页 L C R u uL uC i + - + - + - + - uR R + - + - + - + - . I j L U UL U C . jC 1 UR 返 回

i= 5∠60° =0.149∠-3.4°A Z33.54∠63.4° UR=Ri=15×0.149∠-3.4°=2.235∠-3.4°V 0L=joLi=56.5∠90°×0.149∠-3.4°=8.42∠86.4°V 0c=-j1=26.5∠-90°x0.149∠-3.4°=3.95∠-93.4°V 则 i=0.149N2c0s(ot-3.4)A ug =2.2352cos(@t-3.4)V u,=8.42√2cos(wt+86.6)V u=3.95V2c0s(wt-93.4)V 回 上
0.149 3.4 A 33.54 63.4 5 60 o o o Z U I 则 i 0.149 2cos(ωt 3.4 o ) A 15 0.149 3.4 2.235 3.4 V o o U R RI j 56.5 90 0.149 3.4 8.42 86.4 V o o o U L LI 26.5 90 0.149 3.4 3.95 93.4 V C 1 j o o o U C I 2.235 2cos( 3.4 ) V o uR ω t 8.42 2cos( 86.6 ) V o uL ω t 3.95 2cos( 93.4 ) V o uC ω t 返 回 上 页 下 页
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《电路理论》课程教学课件(讲稿)第8章 相量法.pdf
- 《电路理论》课程教学课件(讲稿)第6章 储能元件.pdf
- 《电路理论》课程教学课件(讲稿)第10章 含有耦合电感的电路.pdf
- 《电路理论》课程教学课件(讲稿)第11章 电路的频率响应.pdf
- 《电路理论》课程教学课件(讲稿)第16章 二端口网络.pdf
- 《电路理论》课程教学课件(讲稿)第12章 三相电路.pdf
- 《电路理论》课程教学课件(讲稿)第13章 非正弦周期电流电路和信号的频谱.pdf
- 安徽大学:《电路理论》课程教学资源(实验指导)电子技术课程设计指导.pdf
- 安徽大学:《电路理论》课程教学资源(实验指导)EDA电路仿真快速入门(Multisim).pdf
- 安徽大学:《电路理论》课程教学资源(实验指导)EDA仿真实验手册.pdf
- 安徽大学:《电路理论》课程课程学习指导(课程重点及难点、典型例题分析、样卷).pdf
- 安徽大学:《电路理论》课程授课教案(讲义,授课教师:寻丽娜).pdf
- 安徽大学:《电路理论》课程教学大纲 Electric Circuits.pdf
- 《电力系统分析》课程教学课件(讲稿)09 电力系统三相短路电流的实用计算.pdf
- 《电力系统分析》课程教学课件(讲稿)08 电力系统三相短路的暂态过程.pdf
- 《电力系统分析》课程教学课件(讲稿)06 电力系统的无功功率和电压调整.pdf
- 《电力系统分析》课程教学课件(讲稿)05 电力系统的有功功率和频率调整.pdf
- 《电力系统分析》课程教学课件(讲稿)10 电力系统各元件的序阻抗和等值电路.pdf
- 《电力系统分析》课程教学课件(讲稿)11 电力系统不对称故障的分析和计算.pdf
- 《电力系统分析》课程教学课件(讲稿)12 电力系统运行稳定性的基本概念.pdf
- 《电路理论》课程教学课件(讲稿)第3章 电组电路的一般分析.pdf
- 《电路理论》课程教学课件(讲稿)第5章 含有运算放大器的电阻电路.pdf
- 《电路理论》课程教学课件(讲稿)第4章 电路定理.pdf
- 《电路理论》课程教学课件(讲稿)第1章 电路模型和电路定律.pdf
- 《电路理论》课程教学课件(讲稿)第2章 电阻电路的等效变换.pdf
- 《机械工程控制基础》课程教学资源(讲稿)第六章 系统的性能与校正.pdf
- 《机械工程控制基础》课程教学资源(讲稿)第三章 时间响应分析.pdf
- 《机械工程控制基础》课程教学资源(讲稿)第二章 系统数学模型.pdf
- 《机械工程控制基础》课程教学资源(讲稿)第一章 绪论.pdf
- 《机械工程控制基础》课程教学资源(讲稿)第五章 系统的稳定性.pdf
- 《机械工程控制基础》课程教学资源(讲稿)第四章 频率特性分析.pdf
- 《机械工程控制基础》课程教学资源(讲稿)第六章 拉氏变换.pdf
- 中国农业大学:《工程测试技术》课程教学大纲(Measuring and Testing in Engineering).pdf
- 中国农业大学:《工程测试技术》课程授课教案(讲义)第二章 传感器.doc
- 中国农业大学:《工程测试技术》课程授课教案(讲义)第一章 测试系统及其基本特性.doc
- 中国农业大学:《工程测试技术》课程授课教案(讲义)第五章 机械工程典型参数测量技术.doc
- 中国农业大学:《工程测试技术》课程授课教案(讲义)第三章 信号的调理、记录和传输.doc
- 中国农业大学:《工程测试技术》课程教学课件(PPT讲稿)第二章 传感器.ppt
- 中国农业大学:《工程测试技术》课程教学课件(PPT讲稿)第一章 测试系统的基本特性.ppt
- 中国农业大学:《工程测试技术》课程教学课件(PPT讲稿)第三章 信号调理.ppt
