《电路理论》课程教学课件（讲稿）第3章 电组电路的一般分析

第3章 电阻电路的一般分析 本章重点 3.1 电路的图 3.2 KCL和KVL的独立方程数 3.3 支路电流法 3.4 网孔电流法 3.5 回路电流法 3.6 结点电压法 首页

第3章 电阻电路的一般分析 3.1 电路的图 3.2 KCL和KVL的独立方程数 3.3 支路电流法 3.4 网孔电流法 3.5 回路电流法 3.6 结点电压法 首 页 本章重点

●重点 熟练掌握电路方程的列写方法： 支路电流法 回路电流法 结点电压法

重点 熟练掌握电路方程的列写方法： 支路电流法 回路电流法 结点电压法

●线性电路的一般分析方法 普遍性：对任何线性电路都适用。 系统性：计算方法有规律可循。 ●方法的基础 电路的连接关系一KCL,KVL定律。 ·元件的电压、电流关系特性。 复杂电路的一般分析法就是根据KCL、KVL及 元件电压和电流关系列方程、解方程。根据列方程 时所选变量的不同可分为支路电流法、回路电流法 和结点电压法

线性电路的一般分析方法 • 普遍性：对任何线性电路都适用。 复杂电路的一般分析法就是根据KCL、KVL及 元件电压和电流关系列方程、解方程。根据列方程 时所选变量的不同可分为支路电流法、回路电流法 和结点电压法。 • 元件的电压、电流关系特性。 • 电路的连接关系—KCL，KVL定律。 方法的基础 • 系统性：计算方法有规律可循

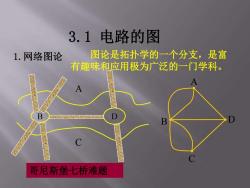
3.1电路的图 1.网络图论 图论是拓扑学的一个分支，是富 有趣味和应用极为广泛的一门学科。 哥尼斯堡七桥难题

1.网络图论 B D A C D C B A 哥尼斯堡七桥难题 图论是拓扑学的一个分支，是富 有趣味和应用极为广泛的一门学科。 3.1 电路的图

2.电路的图 n=5b=8 抛开元 件性质 6 us 一个元件作 元件的串联及并联 为一条支路 组合作为一条支路 n=4b=6 有向图

2.电路的图 抛开元 件性质 一个元件作 为一条支路 n  5 b  8 元件的串联及并联 组合作为一条支路 n  4 b  6 5 4 3 2 1 6 有向图 6 5 4 3 2 1 7 8 R4 R1 R3 R2 R6 uS + _ i R5

乡结论电路的图是用以表示电路几何结构的图 形，图中的支路和结点与电路的支路和结点一一对 应。 (I)图的定义(Graph) G={支路，结点} ①图中的结点和支路各自是一个整体。 ②移去图中的支路，与它所联接的结点依然 存在，因此允许有孤立结点存在。 ③如把结点移去，则应把与它联 接的全部支路同时移去

⑴图的定义(Graph) G={支路，结点} 电路的图是用以表示电路几何结构的图 形，图中的支路和结点与电路的支路和结点一一对 应。 ①图中的结点和支路各自是一个整体。 ②移去图中的支路，与它所联接的结点依然 存在，因此允许有孤立结点存在。 ③如把结点移去，则应把与它联 接的全部支路同时移去。 结论

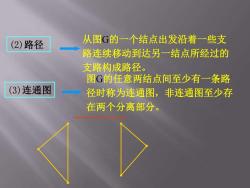
(2)路径 从图G的一个结点出发沿着一些支 路连续移动到达另一结点所经过的 支路构成路径。 图G的任意两结点间至少有一条路 (3)连通图 径时称为连通图，非连通图至少存 在两个分离部分

从图G的一个结点出发沿着一些支 路连续移动到达另一结点所经过的 支路构成路径。 (2)路径 (3)连通图 图G的任意两结点间至少有一条路 径时称为连通图，非连通图至少存 在两个分离部分

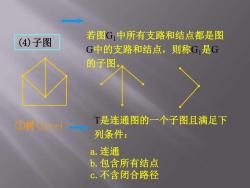
若图G,中所有支路和结点都是图 (4)子图 G中的支路和结点，则称G是G 的子图 ①树(Tree) T是连通图的一个子图且满足下 列条件： a.连通 b.包含所有结点 c.不含闭合路径

(4)子图 若图G1中所有支路和结点都是图 G中的支路和结点，则称G1是G 的子图。 ①树(Tree) T是连通图的一个子图且满足下 列条件： a.连通 b.包含所有结点 c.不含闭合路径

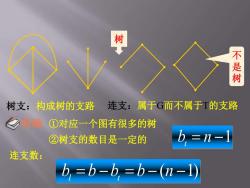
树 不是树 树支：构成树的支路 连支：属于G而不属于T的支路 乡明确 ①对应一个图有很多的树 ②树支的数目是一定的 =n-1 连支数： b,=b-b=b-(n-1)

树支：构成树的支路 连支：属于G而不属于T的支路 ②树支的数目是一定的 连支数： 不 是 树 b  n 1 t b  b  b  b  (n 1) l t 树 明确 ①对应一个图有很多的树

②回路Loop) L是连通图的一个子图，构成一 条闭合路径，并满足：(1)连通， (2)每个结点关联2条支路。 回路 不是回路 明1)对应一个图有很多的回路； 确2)基本回路的数目是一定的，为连支数； 3)对于平面电路，网孔数等于基本回路数。 I=b=b-(n-1)

②回路(Loop) L是连通图的一个子图，构成一 条闭合路径，并满足：(1)连通， 1 (2)每个结点关联2条支路。 2 3 4 5 6 7 8 2 5 3 1 2 4 7 5 8 不 是 回 路 回路 2）基本回路的数目是一定的，为连支数； l  b  b  (n 1) l 1）对应一个图有很多的回路； 3）对于平面电路，网孔数等于基本回路数。 明 确