《电力系统分析》课程教学课件(讲稿)10 电力系统各元件的序阻抗和等值电路
第7章电力系统各元件的序阻抗和等值电路 1、什么是对称分量法? 2、为什么要引入对称分量法? ·对称分量法 分析过程是仕么? ·对称分量法在不对称故 1、各元件的序参数是怎样的? 2、如何绘制电力系统的序网图? ·电力系统元件序参数及系统的序网图
第7章 电力系统各元件的序阻抗和等值电路 •对称分量法 •对称分量法在不对称故障分析计算中的应用 •电力系统元件序参数及系统的序网图 1、什么是对称分量法? 2、为什么要引入对称分量法? 分析过程是什么? 1、各元件的序参数是怎样的? 2、如何绘制电力系统的序网图?
7.1对称分量法在不对称短路计算中的应用 一、对称分量法 Fe.Fco 120° 到 尼 1209 京=序。=戎 Fal 2 o Fa 正序分量 负序分量 零序分量 F60方b2 合成
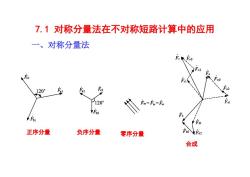
7.1 对称分量法在不对称短路计算中的应用 一、对称分量法 正序分量 负序分量 零序分量 合成

一、对称分量法 ·正序分量:三相量大小相等,互差120°,且与系 统正常运行相序相同。 ·负序分量:三相量大小相等,互差120,且与系 统正常运行相序相反。 ·零序分量:三相量大小相等,相位一致。 一逆时针旋转1200 Fn a"Fa Fa aFa a=ej1209 户0=户=0
一、对称分量法 • 正序分量:三相量大小相等,互差1200,且与系 统正常运行相序相同。 • 负序分量:三相量大小相等,互差1200,且与系 统正常运行相序相反。 • 零序分量:三相量大小相等,相位一致。 0 0 0 2 2 2 2 2 1 1 1 2 1 , , b c a b a c a b a c a F F F F aF F a F F a F F aF j120 a e 逆时针旋转1200

一、对称分量法 ·三相量用三序量表示 户。=fa1+Fa2+Fa0 Fo=Fo+Fo2 +Foo a2Fa +afa2 +Fa a0 1 1 Fe=Fa Fe2 Foo=aFal +a2 Faz+Fao T- a ·三序量用三相量表示 aa 1 Fa 2 F12o=T-Fabe Q Fabe =TF20
一、对称分量法 • 三相量用三序量表示 • 三序量用三相量表示 2 0 2 1 2 0 1 1 2 0 2 1 2 0 1 2 0 c c c c a a a b b b b a a a a a a a F F F F aF a F F F F F F a F aF F F F F F c b a a a a F F F a a a a F F F 1 1 1 1 1 3 1 2 2 0 2 1 1 120 abc F F T 2 2 1 1 1 1 1 a a a a T abc T 120 F F
二、序阻抗的概念 ·静止的三相电路元件序阻抗 a+△Va Zaa Zab a Zaa i西,+Ai Zab bo Zac Zbe Zbb ie H+-AV. Zbe △'abc=ZIabe Z=TZT AV120 =TZTI20 =Zs120 称为序阻抗矩阵
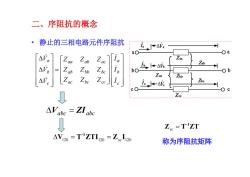
二、序阻抗的概念 • 静止的三相电路元件序阻抗 c b a ac bc cc ab bb bc aa ab ac c b a I I I Z Z Z Z Z Z Z Z Z V V V Vabc ZI abc 120 120 120 sc -1 V T ZTI Z I sc -1 Z T ZT 称为序阻抗矩阵

二、序阻抗的概念 ·当元件参数完全对称时二a=26b=2cc=2,2b=2c=2ca=二m 「Z-Zm 0 0 Z. 0 0 2z z.+2z0 △'a=Zial 4Y120=ZcI120 AVa2 =Z2ia2 AVao=Zoia0 结论:在三相参数对称的线性电路中,各序对称分量具有独 立性,因此,可以对正序、负序、零序分量分别进行计算
• 当元件参数完全对称时 二、序阻抗的概念 aa bb cc s ab bc ca m z z z z z z z z 0 2 1 0 0 0 0 0 0 0 0 2 0 0 0 0 Z Z Z Z Z Z Z Z Z Z s m s m s m sc 120 120 V Z I sc 0 0 0 2 2 2 1 1 1 a a a a a a V Z I V Z I V Z I 结论:在三相参数对称的线性电路中,各序对称分量具有独 立性,因此,可以对正序、负序、零序分量分别进行计算

二、序阻抗的概念 ·序阻抗:元件三相参数对称时,元件两端某一序的电压降 与通过该元件的同一序电流的比值。 正序阻抗一Z1=△广ai/ial 负序阻抗一Z2=A广a2/ia2 零序阻抗一Z0=A0/i0
二、序阻抗的概念 • 序阻抗:元件三相参数对称时,元件两端某一序的电压降 与通过该元件的同一序电流的比值。 0 0 0 2 2 2 1 1 1 / / / a a a a a a Z V I Z V I Z V I 正序阻抗 负序阻抗 零序阻抗
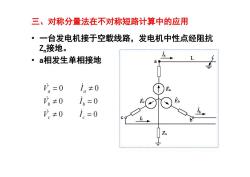
三、对称分量法在不对称短路计算中的应用 ·一台发电机接于空载线路,发电机中性点经阻抗 Zn接地。 ·a相发生单相接地 。=0 i。≠0 。≠0 i。=0 可≠0 i。=0
三、对称分量法在不对称短路计算中的应用 • 一台发电机接于空载线路,发电机中性点经阻抗 Zn接地。 • a相发生单相接地 0 0 0 0 0 0 c c b b a a V I V I V I
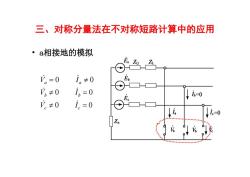
三、对称分量法在不对称短路计算中的应用 ·a相接地的模拟 。=0 in≠0 。≠0 i。=0 ↓-0 。≠0 i。=0
三、对称分量法在不对称短路计算中的应用 • a相接地的模拟 0 0 0 0 0 0 c c b b a a V I V I V I
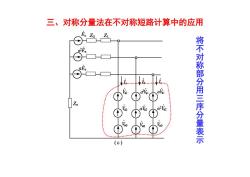
三、对称分量法在不对称短路计算中的应用 Z 2 将不对称部分用三序分量表示 (c)
三、对称分量法在不对称短路计算中的应用 将 不 对 称 部 分 用 三 序 分 量 表 示
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《电力系统分析》课程教学课件(讲稿)11 电力系统不对称故障的分析和计算.pdf
- 《电力系统分析》课程教学课件(讲稿)12 电力系统运行稳定性的基本概念.pdf
- 《电力系统分析》课程教学课件(讲稿)13 电力系统暂态稳定性.pdf
- 《电力系统分析》课程教学课件(讲稿)04 复杂电力系统潮流的计算机算法.pdf
- 《电力系统分析》课程教学课件(讲稿)14 电力系统静态稳定性.pdf
- 《电力系统分析》课程教学课件(讲稿)03 简单电力网络的计算和分析.pdf
- 《电力系统分析》课程教学课件(讲稿)02 电力系统各元件的特性和数学模型.pdf
- 《电力系统分析》课程教学课件(讲稿)01 电力系统的基本概念.pdf
- 《电力系统分析》课程教学课件(PPT讲稿)第三章 同步发电机的基本方程.ppt
- 《电力系统分析》课程教学实验指导书.doc
- 《电力系统分析》课程教学资源(书籍文献)电力系统稳定与控制(Kundur,中文版).pdf
- 《电力系统分析》课程教学资源(书籍文献)电力系统分析课后习题答案(第三版,何仰赞).pdf
- 《电力系统分析》课程教学资源(书籍文献)电力系统分析韩祯祥(浙大经典).pdf
- 《电力系统分析》课程教学资源(书籍文献)电力系统电压稳定 Power System Voltage Stability[美]CARSON W.TAYLOR.pdf
- 《电力系统分析》课程教学资源(习题解答)电力系统分析下册.pdf
- 《电力系统分析》课程教学资源(习题解答)电力系统分析上册.pdf
- 《电力系统分析》课程作业习题(含参考答案).doc
- 《电力系统分析》课程教学大纲 Power System Analysis(二).doc
- 《电力系统分析》课程教学大纲 Power System Analysis(一).doc
- 《电力系统分析》课程设计学大纲 Comprehensuve Course Design of Power System.doc
- 《电力系统分析》课程教学课件(讲稿)05 电力系统的有功功率和频率调整.pdf
- 《电力系统分析》课程教学课件(讲稿)06 电力系统的无功功率和电压调整.pdf
- 《电力系统分析》课程教学课件(讲稿)08 电力系统三相短路的暂态过程.pdf
- 《电力系统分析》课程教学课件(讲稿)09 电力系统三相短路电流的实用计算.pdf
- 安徽大学:《电路理论》课程教学大纲 Electric Circuits.pdf
- 安徽大学:《电路理论》课程授课教案(讲义,授课教师:寻丽娜).pdf
- 安徽大学:《电路理论》课程课程学习指导(课程重点及难点、典型例题分析、样卷).pdf
- 安徽大学:《电路理论》课程教学资源(实验指导)EDA仿真实验手册.pdf
- 安徽大学:《电路理论》课程教学资源(实验指导)EDA电路仿真快速入门(Multisim).pdf
- 安徽大学:《电路理论》课程教学资源(实验指导)电子技术课程设计指导.pdf
- 《电路理论》课程教学课件(讲稿)第13章 非正弦周期电流电路和信号的频谱.pdf
- 《电路理论》课程教学课件(讲稿)第12章 三相电路.pdf
- 《电路理论》课程教学课件(讲稿)第16章 二端口网络.pdf
- 《电路理论》课程教学课件(讲稿)第11章 电路的频率响应.pdf
- 《电路理论》课程教学课件(讲稿)第10章 含有耦合电感的电路.pdf
- 《电路理论》课程教学课件(讲稿)第6章 储能元件.pdf
- 《电路理论》课程教学课件(讲稿)第8章 相量法.pdf
- 《电路理论》课程教学课件(讲稿)第9章 正弦稳态电路的分析.pdf
- 《电路理论》课程教学课件(讲稿)第3章 电组电路的一般分析.pdf
- 《电路理论》课程教学课件(讲稿)第5章 含有运算放大器的电阻电路.pdf
