《电力系统分析》课程教学课件(讲稿)09 电力系统三相短路电流的实用计算

第六章电力系统三相短路电流的实用计算 6.1短路电流计算的基本原理和方法 6.2起始次暂态电流和冲击电流的实用计算 6.3短路电流计算曲线及其应用 6.4短路电流周期分量的近似计算 2015-1-2 电力系统分析第六章
2015-1-2 电力系统分析 第六章 1 第六章 电力系统三相短路电流的实用计算 6.1 短路电流计算的基本原理和方法 6.2 起始次暂态电流和冲击电流的实用计算 6.3 短路电流计算曲线及其应用 6.4 短路电流周期分量的近似计算
6.1短路电流计算的基本原理和方法 电力系统节点方程的建立 计算机实现 利用节点阻抗矩阵计算短路电流 利用电势源对短路点的转移阻抗计算短路电流一> 1. 网络等值变换 手算;复杂、 简单网络 2. 分裂电势源、分裂短路点 3. 利用网络结构对称性 网络化简 4. 电流分布系数 单位电流法 手算、简单网络 ■ 网络还原法 2015-1-2 电力系统分析第六章
2015-1-2 电力系统分析 第六章 2 电力系统节点方程的建立 利用节点阻抗矩阵计算短路电流 利用电势源对短路点的转移阻抗计算短路电流 1. 网络等值变换 2. 分裂电势源、分裂短路点 3. 利用网络结构对称性 4. 电流分布系数 单位电流法 网络还原法 6.1 短路电流计算的基本原理和方法 计算机实现 手算;复杂、 简单网络 手算、简单网络 网络化简
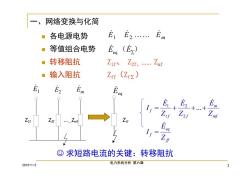
一、 网络变换与化简 ■各电源电势 Em E1E2. ·等值组合电势 E(E2) 转移阻抗 Z1f、Z2f、.Zt ·输入阻抗 Zt(Zx) E E2 I= Zi 它十十 Zu .Zm Zs ©求短路电流的关键:转移阻抗 2015-1-2 电力系统分析第六章
2015-1-2 电力系统分析 第六章 3 各电源电势 等值组合电势 转移阻抗 Z1f、 Z2f、. Zmf 输入阻抗 Zff(Zf∑) 一、网络变换与化简 E1 E 2 Em E eq(E) 求短路电流的关键:转移阻抗

网络变换和化简几种方法 1. 网络的等值变换 ①有阻抗支路串联、并联—一常用 ② 无源网络的星网变换 ③有源支路的并联 分裂电势源和分裂短路点 3. 利用网络结构对称性 4. 电流分布系数法 2015-1-2 电力系统分析第六章
2015-1-2 电力系统分析 第六章 4 网络变换和化简几种方法 1. 网络的等值变换 ① 有阻抗支路串联、并联——常用 ② 无源网络的星网变换 ③ 有源支路的并联 2. 分裂电势源和分裂短路点 3. 利用网络结构对称性 4. 电流分布系数法
1、网络的等值变换 网络的等值变换原则: ① 变换前后,节点电压分布不变。 ② 自网络外部流向该节点电流不变。 注意:以下变化,假设各支路间不存在互感的线性网络 2015-1-2 电力系统分析第六章
2015-1-2 电力系统分析 第六章 5 1、网络的等值变换 ① 变换前后,节点电压分布不变。 ② 自网络外部流向该节点电流不变。 网络的等值变换原则: 注意:以下变化,假设各支路间不存在互感的线性网络
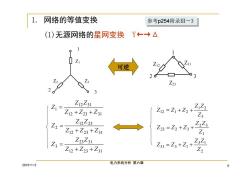
1. 网络的等值变换 参考p254附录IⅢ-3 (1)无源网络的星网变换Y←→△ 可逆 26 Z23 2。 ZI= Z12Z31 12+Z23+Z31 Z12=Z1+Z2+ ZiZ2 Z2= Z12Z23 Z23=Z2+Z3+ Z2Z3 Z12+Z23+Z31 Z Z3= Z23Z31 Z:Zi Z12+Z23+Z31 Z31=Z3+Z1+ Z2 2015-1-2 电力系统分析第六章 6
2015-1-2 电力系统分析 第六章 6 1. 网络的等值变换 (1)无源网络的星网变换 可逆 12 23 31 23 31 3 12 23 31 12 23 2 12 23 31 12 31 1 Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z 2 3 1 31 3 1 1 2 3 23 2 3 3 1 2 12 1 2 Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Y←→Δ 参考参考p254附录Ⅲ-3 p254附录Ⅲ-3
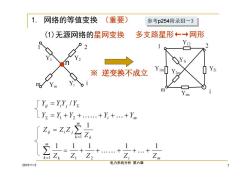
1. 网络的等值变换 (重要) 参考p254附录Ⅲ-3 (1)无源网络的星网变换 多支路星形←→网形 12 ※逆变换不成立 Yim Ym Y=YY,IYs 人Y2=Y+Y2+.+Y,+.+Ym 1 +.+ +.十 ZZ Z, Zm 2015-1-2 电力系统分析第六章 >
2015-1-2 电力系统分析 第六章 7 多支路星形←→网形 ※ 逆变换不成立 1. 网络的等值变换 (重要) (1)无源网络的星网变换 i m m k k m k k ij i j Z Z Z Z Z Z Z Z Z 1 1 1 1 1 1 1 1 2 1 i m ij i j Y Y Y Y Y Y Y Y Y 1 2 / n 参考参考p254附录Ⅲ-3 p254附录Ⅲ-3
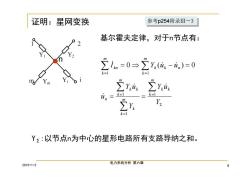
证明:星网变换 参考p254附录Ⅲ-3 基尔霍夫定律,对于n节点有: g.-0-2xaa)-0 k=1 YΣ:以节点n为中心的星形电路所有支路导纳之和。 2015-1-2 电力系统分析第六章
2015-1-2 电力系统分析 第六章 8 证明:星网变换 n 基尔霍夫定律,对于n节点有: Y Y u Y Y u u I Y u u m k k k m k k m k k k n m k k k n m k kn 1 1 1 1 1 0 ( ) 0 YΣ:以节点n为中心的星形电路所有支路导纳之和。 参考参考p254附录Ⅲ-3 p254附录Ⅲ-3
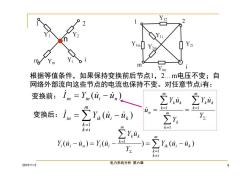
m 根据等值条件,如果保持变换前后节点1,2.m电压不变;自 网络外部流向这些节点的电流也保持不变。对任意节点有: 变换前:in=Yn(u,-un) ,4 k=1 变换后: in=∑y(a,-i) un = Y k=1 y. k=1 k≠i Y(u-in)=Y(i Y Yu (u-ug) k=1 k≠i 2015-1-2 电力系统分析第六章
2015-1-2 电力系统分析 第六章 9 n 根据等值条件,如果保持变换前后节点1,2.m电压不变;自 网络外部流向这些节点的电流也保持不变。对任意节点i有: ( ) ( ) 1 i k m k i k in ik in in i n I Y u u I Y u u ( ) ( ) ( ) 1 1 m k i k ik i k m k k k i i n i i Y u u Y Y u Y u u Y u 变换前: 变换后: Y Y u Y Y u u m k k k m k k m k k k n 1 1 1

ram-Yam n2r-ri r.2r(u-i) Y( k=1 )=Y(L k=1 k=1 Y y∑y(位,-) k=1 Y 变换前 变换后 若第j项系数相等,该式对任意电压值都相等j丰1 .Ya-2=y,(a,-) Y .Y=YY,IYs 2=2,2 2015-1-2 电力系统分析第六章 10
2015-1-2 电力系统分析 第六章 10 Y Y Y u u Y u Y Y u Y Y Y u Y u Y i k m k i k m k k k m k i k i m k i k k i ( ) ) ) 1 1 1 1 ( ( ( ) ( ) 1 1 m k i k ik i k i k m k i k Y u u Y Y Y u u 变换前 变换后 若第j项系数相等,该式对任意电压值都相等j≠i ij i j) i j i j Y u u Y Y Y u u ( ( ) Yij YiYj Y / m k k ij i j Z Z Z Z 1 1
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《电力系统分析》课程教学课件(讲稿)08 电力系统三相短路的暂态过程.pdf
- 《电力系统分析》课程教学课件(讲稿)06 电力系统的无功功率和电压调整.pdf
- 《电力系统分析》课程教学课件(讲稿)05 电力系统的有功功率和频率调整.pdf
- 《电力系统分析》课程教学课件(讲稿)10 电力系统各元件的序阻抗和等值电路.pdf
- 《电力系统分析》课程教学课件(讲稿)11 电力系统不对称故障的分析和计算.pdf
- 《电力系统分析》课程教学课件(讲稿)12 电力系统运行稳定性的基本概念.pdf
- 《电力系统分析》课程教学课件(讲稿)13 电力系统暂态稳定性.pdf
- 《电力系统分析》课程教学课件(讲稿)04 复杂电力系统潮流的计算机算法.pdf
- 《电力系统分析》课程教学课件(讲稿)14 电力系统静态稳定性.pdf
- 《电力系统分析》课程教学课件(讲稿)03 简单电力网络的计算和分析.pdf
- 《电力系统分析》课程教学课件(讲稿)02 电力系统各元件的特性和数学模型.pdf
- 《电力系统分析》课程教学课件(讲稿)01 电力系统的基本概念.pdf
- 《电力系统分析》课程教学课件(PPT讲稿)第三章 同步发电机的基本方程.ppt
- 《电力系统分析》课程教学实验指导书.doc
- 《电力系统分析》课程教学资源(书籍文献)电力系统稳定与控制(Kundur,中文版).pdf
- 《电力系统分析》课程教学资源(书籍文献)电力系统分析课后习题答案(第三版,何仰赞).pdf
- 《电力系统分析》课程教学资源(书籍文献)电力系统分析韩祯祥(浙大经典).pdf
- 《电力系统分析》课程教学资源(书籍文献)电力系统电压稳定 Power System Voltage Stability[美]CARSON W.TAYLOR.pdf
- 《电力系统分析》课程教学资源(习题解答)电力系统分析下册.pdf
- 《电力系统分析》课程教学资源(习题解答)电力系统分析上册.pdf
- 安徽大学:《电路理论》课程教学大纲 Electric Circuits.pdf
- 安徽大学:《电路理论》课程授课教案(讲义,授课教师:寻丽娜).pdf
- 安徽大学:《电路理论》课程课程学习指导(课程重点及难点、典型例题分析、样卷).pdf
- 安徽大学:《电路理论》课程教学资源(实验指导)EDA仿真实验手册.pdf
- 安徽大学:《电路理论》课程教学资源(实验指导)EDA电路仿真快速入门(Multisim).pdf
- 安徽大学:《电路理论》课程教学资源(实验指导)电子技术课程设计指导.pdf
- 《电路理论》课程教学课件(讲稿)第13章 非正弦周期电流电路和信号的频谱.pdf
- 《电路理论》课程教学课件(讲稿)第12章 三相电路.pdf
- 《电路理论》课程教学课件(讲稿)第16章 二端口网络.pdf
- 《电路理论》课程教学课件(讲稿)第11章 电路的频率响应.pdf
- 《电路理论》课程教学课件(讲稿)第10章 含有耦合电感的电路.pdf
- 《电路理论》课程教学课件(讲稿)第6章 储能元件.pdf
- 《电路理论》课程教学课件(讲稿)第8章 相量法.pdf
- 《电路理论》课程教学课件(讲稿)第9章 正弦稳态电路的分析.pdf
- 《电路理论》课程教学课件(讲稿)第3章 电组电路的一般分析.pdf
- 《电路理论》课程教学课件(讲稿)第5章 含有运算放大器的电阻电路.pdf
- 《电路理论》课程教学课件(讲稿)第4章 电路定理.pdf
- 《电路理论》课程教学课件(讲稿)第1章 电路模型和电路定律.pdf
- 《电路理论》课程教学课件(讲稿)第2章 电阻电路的等效变换.pdf
- 《机械工程控制基础》课程教学资源(讲稿)第六章 系统的性能与校正.pdf
