《电路理论》课程教学课件（讲稿）第11章 电路的频率响应

第11章电路的频率响应 本章重点 11.1 网络函数 11.2 RLC串联电路的谐振 11.3 RLC串联电路的频率响应 11.4 RLC并联谐振电路 11.5 波特图 11.6 浅波器简介 首页

第11章 电路的频率响应 11.1 网络函数 11.2 RLC串联电路的谐振 11.3 RLC串联电路的频率响应 11.4 RLC并联谐振电路 11.5 波特图 11.6 滤波器简介 本章重点 首 页

●重点 1.网络函数 2.串、并联谐振的概念； 国

重点 1. 网络函数 2. 串、并联谐振的概念； 返 回

11.1网络函数 当电路中激励源的频率变化时，电路中的感抗、 容抗将跟随频率变化，从而导致电路的工作状态亦 跟随频率变化。因此，分析研究电路和系统的频率 特性就显得格外重要。 频率特性 电路和系统的工作状态跟随频率而变化的现象， 称为电路和系统的频率特性，又称频率响应。 1.网络函数H(jω)的定义

11.1 网络函数 当电路中激励源的频率变化时，电路中的感抗、 容抗将跟随频率变化，从而导致电路的工作状态亦 跟随频率变化。因此，分析研究电路和系统的频率 特性就显得格外重要。 上 页 下 页 频率特性 电路和系统的工作状态跟随频率而变化的现象， 称为电路和系统的频率特性，又称频率响应。 1. 网络函数H（jω）的定义 返 回

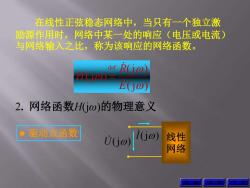
在线性正弦稳态网络中，当只有一个独立激 励源作用时，网络中某一处的响应（电压或电流） 与网络输入之比，称为该响应的网络函数。 def R(iO 10 2.网络函数H(Gjω)的物理意义 ·驱动点函数 线性 网络

在线性正弦稳态网络中，当只有一个独立激 励源作用时，网络中某一处的响应（电压或电流） 与网络输入之比，称为该响应的网络函数。 (j ) (j ) (j ) def    E R H    2. 网络函数H(jω)的物理意义  驱动点函数 线性 网络 I(j)  U(j)  返 回 上 页 下 页

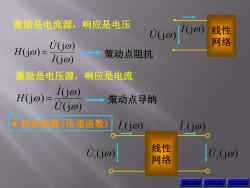
激励是电流源，响应是电压 V(o i(j@) 线性 0(jo) 网络 H(j@)= i(jo) 策动点阻抗 激励是电压源， 响应是电流 H(j@)= i(jo) 一→策动点导纳 U(j@ ●转移函数（传递函数） I(o) I(j) U(j@) 线性 网络 U.jw

(j ) (j ) (j )    I U H    策动点阻抗 策动点导纳 激励是电流源，响应是电压 激励是电压源，响应是电流 (j ) (j ) (j )    U I H    线性 网络 I(j)  U(j)   转移函数(传递函数) (j ) U  1  线性 网络 (j ) U  2  (j ) I  1  (j ) I  2  返 回 上 页 下 页

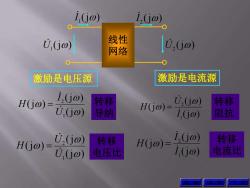
i(j) 0,jo) 线性 网络 U.(j0) Q 激励是电压源 激励是电流源 H(j@)= i,(jo) 转移 U,(j0） 转移 0,Go) 导纳 H(G0)= I(jo) 阻抗 H0o)= 0,(jo) 转移 U(jo) 电压比 H(j@)- i(j@) 转移 i(j@ 电流比

转移 导纳 转移 阻抗 转移 电压比 转移 电流比 激励是电压源 激励是电流源 (j ) U  1  线性 网络 (j ) U  2  (j ) I  1  (j ) I  2  (j ) (j ) (j ) 1 2    I U H    (j ) (j ) (j ) 1 2    U I H    (j ) (j ) (j ) 1 2    U U H    (j ) (j ) (j ) 1 2    I I H    返 回 上 页 下 页

淮意 ①H(Go)与网络的结构、参数值有关，与输入、输出 变量的类型以及端口对的相互位置有关，与输入、 输出幅值无关。因此网络函数是网络性质的一种 体现。 ②H(G0是一个复数，它的频率特性分为两个部分： 幅频特性 模与频率的关系HGo)~0 相频特性 幅角与频率的关系pG0)~0 ③®网络函数可以用相量法中任一分析求解方法获得

注意  H(j)与网络的结构、参数值有关，与输入、输出 变量的类型以及端口对的相互位置有关，与输入、 输出幅值无关。因此网络函数是网络性质的一种 体现。  H(j) 是一个复数，它的频率特性分为两个部分： 幅频特性 模与频率的关系 | H(j) |~  相频特性 幅角与频率的关系 (j) ~  网络函数可以用相量法中任一分析求解方法获得。 返 回 上 页 下 页

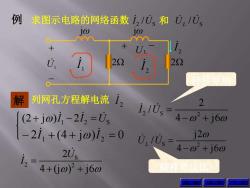
例 求图示电路的网络函数i,/U和：U/0§ 10 解 列网孔方程解电流 2 (2+jo)i,-2i2=U、 i,10=4-02+j60 -2i1+(4+jo)12=0 j20 2Us U,10s=4-02+j60 i,=4+00+j60 传移电压 回

例 求图示电路的网络函数 2 S I U/   S / U U L 和   L . U U1  2 jω + _ + _ jω 2 2 I  1 I  2 I  解 列网孔方程解电流 2 I  1 2 S (2 j ) 2     I I U     2I 1  (4  j )I 2  0    S 2 2 2 4 (j ) j6 U I        2 S 2 2 / 4 j6 I U        S 2 j 2 / 4 j6 U U L         转移导纳 转移电压比 返 回 上 页 下 页

乡注意①以网络函数中j的最高次方的次数定义网 络函数的阶数。 ②由网络函数能求得网络在任意正弦输入时 的端口正弦响应，即有 H(j@)= R(jo) → E(j) R(jo)=H(j@)E(j@) 回

①以网络函数中jω的最高次方的次数定义网 络函数的阶数。 R(j) H(j)E(j)    注意 ②由网络函数能求得网络在任意正弦输入时 的端口正弦响应，即有 (j ) (j ) (j )    E R H    返 回 上 页 下 页

11.2RLC串联电路的谐振 谐振是正弦电路在特定条件下产生的一种特殊 物理现象。谐振现象在无线电和电工技术中得到广 泛应用，研究电路中的谐振现象有重要实际意义。 1.谐振的定义 含R、L、C的一端口电路，在特定条件下出现端 口电压、电流同相位的现象时，称电路发生了谐振。 R,L,C ù 电路 -Z-R 回

11.2 RLC串联电路的谐振 谐振是正弦电路在特定条件下产生的一种特殊 物理现象。谐振现象在无线电和电工技术中得到广 泛应用，研究电路中的谐振现象有重要实际意义。 含R、L、C的一端口电路，在特定条件下出现端 口电压、电流同相位的现象时，称电路发生了谐振。 1. 谐振的定义 R,L,C U 电路  I  Z R I U     发生 谐振 返 回 上 页 下 页