《机械工程控制基础》课程教学资源（讲稿）第二章 系统数学模型

第二章系统的数学模型 基本内容 2.0概述 系统按其微分方程是否线性这一特性，可以分为线性系统和 非线性系统。如果系统的运动状态能用线性微分方程表示，则此 系统为线性系统。线性系统的一个最重要的特性就是满足叠加原 理。线性系统又可分为线性定常系统和线性时变系统。 系统的数学模型是系统动态特性的数学描述。对于同一系 统，数学模型可以有多种形式，如微分方程、传递函数、单位脉 冲响应函数及频率特性等等。但系统是否线性这一特性，不会随 模型形式的不同而改变。线性与非线性是系统的固有特性，完全 由系统的结构与参数确定。 系统建模是经典控制理论和现代控制理论的基础。建立系统 数学模型的方法有分析法和实验辨识法两种。前者主要用于对系 统结构及参数的认识都比较清楚的简单系统，而后者通常用于对 系统结构和参数有所了解，而需进一步精化系统模型的情况。对 于复杂系统的建模往往是一个分析法与实验辨识法相结合的多 次反复的过程。在建模的过程中还要正确处理模型简化和模型精 度的辨证关系，以建立简单且能满足要求的数学模型。 2.1系统的微分方程 列写系统或元件微分方程的一般步骤为： (1).确定系统或元件的输入量和输出量： (2).按照信号的传递顺序，从系统的输入端出发，根据有关

第二章 系统的数学模型 基本内容 2.0 概述 系 统 按 其 微 分 方 程 是 否 线 性 这 一 特 性 ，可 以 分 为 线 性 系 统 和 非 线 性 系 统 。如 果 系 统 的 运 动 状 态 能 用 线 性 微 分 方 程 表 示 ，则 此 系 统 为 线 性 系 统 。线 性 系 统 的 一 个 最 重 要 的 特 性 就 是 满 足 叠 加 原 理。线性系统又可分为线性定常系统和线性时变系统。 系统的数学模型是系统动态特性的数学描述。对于同一系 统，数学模型可以有多种形式，如微分方程、传递函数、单位脉 冲 响 应 函 数 及 频 率 特 性 等 等 。但 系 统 是 否 线 性 这 一 特 性 ，不 会 随 模 型 形 式 的 不 同 而 改 变 。线 性 与 非 线 性 是 系 统 的 固 有 特 性 ，完 全 由系统的结构与参数确定。 系 统 建 模 是 经 典 控 制 理 论 和 现 代 控 制 理 论 的 基 础 。建 立 系 统 数 学 模 型 的 方 法 有 分 析 法 和 实 验 辨 识 法 两 种 。前 者 主 要 用 于 对 系 统 结 构 及 参 数 的 认 识 都 比 较 清 楚 的 简 单 系 统 ，而 后 者 通 常 用 于 对 系 统 结 构 和 参 数 有 所 了 解 ，而 需 进 一 步 精 化 系 统 模 型 的 情 况 。对 于复杂系统的建模往往是一个分析 法与实验辨识法相结合的多 次 反 复 的 过 程 。在 建 模 的 过 程 中 还 要 正 确 处 理 模 型 简 化 和 模 型 精 度的辨证关系，以建立简单且能满足要求的数学模型。 2.1 系统的微分方程 列写系统或元件微分方程的一般步骤为： (1).确定系统或元件的输入量和输出量； (2).按照信号的传递顺序，从系统的输入端出发，根据有关

定律，列写出各个环节的动态微分方程： (3).消除上述各方程式中的中间变量，最后得到只包含输入 量与输出量的方程式： (4).将与输入有关的项写在微分方程的右边，与输出有关的 项写在微分方程的左边，并且各阶导数项按降幂排列。 在列写微分方程的各步中，关键在于掌握组成系统的各个元 件或环节所遵循的有关定律。对于机械类的读者，往往需要列写 机械系统和电网络系统的微分方程，因此，有必要掌握如表21.1 所示的常见元件的物理定律。 表2.1.1常见元件的物理定律 系统元件名称 符号 所遵循的物理定律 类别 及代号 质量元件 人 f=m 机械 m 系统 弹性元件 (直 k w面 f=k(x-x) 线运 动) 阻尼元件 f=c(元2-) c 电容 i=C(2-) C 电感 系 L (-)=L 电阻 R i=R,-) 如果系统中包含非本质非线性的元件或环节，为研究系统方

定律，列写出各个环节的动态微分方程； (3).消除上述各方程式中的中间变量，最后得到只包含输入 量与输出量的方程式； (4).将与输入有关的项写在微分方程的右边，与输出有关的 项写在微分方程的左边，并且各阶导数项按降幂排列。 在列写微分方程的各步中，关键在于掌握组成系统的各个元 件或环节所遵循的有关定律。对于机械类的读者，往往需要列写 机械系统和电网络系统的微分方程，因此，有必要掌握如表 2.1.1 所示的常见元件的物理定律。 表 2.1.1 常见元件的物理定律 系 统 类 别 元件名称 及代号 符 号 所遵循的物理定律 质量元件 m f = m& x& 弹性元件 k ( ) 2 1 f = k x − x 机 械 系 统 （ 直 线 运 动 ） 阻尼元件 c ( ) 2 1 f = c x& − x& 电 容 C ( ) 2 1 i = C v& − v& 电 感 L dt di (v2 − v1 ) = L 电 网 络 系 统 电 阻 R ( ) 1 2 1 v v R i = − 如果系统中包含非本质非线性的元件或环节，为研究系统方

便，通常可将其进行线性化。非线性系统线性化的方法是将变量 的非线性函数在系统某一工作点（或称平衡点）附近展开成泰勒 级数，分解成这些变量在该工作点附近的微增量表达式，然后略 去高于一阶增量的项，并将其写成增量坐标表示的微分方程。 2.2系统的传递函数 一、传递函数 对于线性定常系统，传递函数是一种常用的数学模型。其定 义为：在零初始条件下，系统输出的Laplace变换与引起该输出 的输入量的Laplace变换之比。 若线性定常系统输入x,)与输出x,)之间关系的微分方程为 ag)+a。0++ai0+a0=bm0）+b-m-0+.+0+x0）(2.2.1) 则，系统以x,)为输出、x,)为输入的传递函数可表示成： 8格n (2.2.2) 系统的零初始条件有两方面的含义，一是指在1=0.时输入x,) 才开始作用于系统，因此，1=0时，x,)及其各阶导数均为零： 二是指在1=0时系统处于相对静止的状态，即系统在工作点上运 行，因此1=0时，输出x,)及其各阶导数也均为零。现实的工程 控制系统多属此类情况。 传递函数具有以下特点： (1)传递函数的分母反映了由系统的结构与参数所决定的系 统的固有特性，而其分子则反映了系统与外界之间的联系。 (2)当系统在初始状态为零时，对于给定的输入，系统输出 的Laplace变换完全取决于其传递函数。一旦系统的初始状态不 为零，则传递函数不能完全反映系统的动态历程

便 ，通常可将其进行线性化。非线性系统线性化的方法是将变量 的非线性函数在系统某一工作点（或称平衡点）附近展开成泰勒 级数，分解成这些变量在该工作点附近的微增量表达式，然后略 去高于一阶增量的项，并将其写成增量坐标表示的微分方程。 2.2 系统的传递函数 一、传递函数 对于线性定常系统，传递函数是一种 常用的数学模型。其定 义为： 在零初始条件下， 系统输出的 Laplace 变换与引起该输出 的输入量的 Laplace 变换之比。 若线性定常系统输入 xi (t)与输出 o 之间关系的微分方程为 n o n−1 o 1 o 0 o m i m−1 i 1 i 0 i o i x (t) ( ) ( ) . ( ) ( ) ( ) ( ) . ( ) ( ) ( ) ( 1) ( ) ( 1) a x t a x t a x t a x t b x t b x t b x t b x t n n m m + + + + = + + + + − − & & (2.2.1) 则，系统以 x (t)为输出、 x (t)为输入的传递函数可表示成： 1 0 1 1 1 0 1 1 . . ( ) ( ) ( ) a s a s a s a b s b s b s b X s X s G s n n n n m m m m i o + + + + + + + + = = − − − − (n ≥ m) ( 2.2.2) 系统的零初始条件有两方面的含义，一是指在 时输入 才开始作用于系统，因此， 时 ， 及其各阶导数均为零； 二是指在 时系统处于相对静止的状态，即系统在工作点上运 行，因此 时，输出 及其各阶导数也均为零。现实的工程 控制系统多属此类情况。 = 0 − t x (t) i = 0 − t x (t) i = 0 − t = 0 − t x (t) o 传递函数具有以下特点： (1)传递函数的分母反映了由系统的 结构与参数所决定的系 统的固有特性，而其分子则反映了系统与外界之间的联系。 (2)当系统在初始状态为零时，对于 给定的输入，系统输出 的 Laplace 变换完全取决于其传递函数。 一旦系统的初始状态不 为零，则传递函数不能完全反映系统的动态历程

(3)传递函数分子中s的阶次不会大于分母中s的阶次。 (4)传递函数有无量纲和取何种量纲，取决于系统输出的量 纲与输入的量纲。 (5)不同用途、不同物理组成的不同类型系统、环节或元件 可以具有相同形式的传递函数。 (6)传递函数非常适用于对单输入、单输出线性定常系统的 动态特性进行描述。但对于多输入、多输出系统，需要对不同的 输入量和输出量分别求传递函数。另外，系统传递函数只表示系 统输入量和输出量的数学关系（描述系统的外部特性），而未表 示系统中间变量之间的关系（描述系统的内部特性）。针对这个 局限性，在现代控制理论中，往往采用状态空间描述法对系统的 动态特性进行描述。 二、传递函数的零点、极点和放大系数 传递函数是一个复变函数，一般具有零点、极点。根据复变 函数知识，凡能使复变函数为0的点均称为零点：凡能使复变函 数为趋于∞的点均称为极点。 若将传递函数写成如下的形式： 6- K为常数 则，s=U=1,2,m)为传递函数的零点，s=p,=12,n)为传递函数 的极点，而将K称为系统的放大系数。传递函数的零点和极点的 分布影响系统的动态性能。一般极点影响系统的稳定性，零点影 响系统的瞬态响应曲线的形状。系统的放大系数决定了系统的稳 态输出值。因此，对系统的研究可变成对系统传递函数的零点、 极点和放大系数的研究。 三、典型环节的传递函数 系统是由若干典型环节组成的。常见典型环节及其传递函数 的一般表达式分别为： 比例环节 G(s)=K

(3)传递函数分子中 s 的阶次不会大于分母中 s 的阶次。 (4)传递函数有无量纲和取何种量纲 ，取决于系统输出的量 纲与输入的量纲。 (5)不同用途、 不同物理组成的不同类型系统、 环节或元件， 可以具有相同形式的传递函数。 (6)传递函数非常适用于对单输入、 单输出线性定常系统的 动态特性进行描述。但对于多输入、多输出系统，需要对不同的 输入量和输出量分别求传递函数。另外，系统传递函数只表示系 统输入量和输出量的数学关系（描述系统的外部特性），而未表 示系统中间变量之间的关系（描述系统的内部特性）。针对这个 局限性，在现代控制理论中，往往采用状态空间描述法对系统的 动态特性进行描述。 二、传递函数的零点、极点和放大系数 传递函数是一个复变函数，一般具有零点、极点。根据复变 函数知识，凡能使复变函数为 0 的点均称为零点；凡能使复变函 数为趋于∞的点均称为极点。 若将传递函数写成如下的形式： K为常数 (s p )(s p ).(s p ) K(s z )(s z ).( s z ) G(s ) n m − − − − − − = 1 2 1 2 则 ， s = z j ( j = 1,2,., m)为传递函数的零点， s p ( j 1,2,., n) = j = 为传递函数 的极点， 而 将 K 称为系统的放大系数。 传递函数的零点和极点的 分布影响系统的动态性能。一般极点影响系统的稳定性，零点影 响系统的瞬态响应曲线的形状。系统的放大系数决定了系统的稳 态输出值。因此，对系统的研究可变成对系统传递函数的零点、 极点和放大系数的研究。 三、典型环节的传递函数 系统是由若干典型环节组成的。常见典型环节及其传递函数 的一般表达式分别为： 比例环节 G(s) = K

一阶惯性环节 G(s)=Ts+1 1 积分环节 G6)-元 微分环节 G(s)=Ts 振荡环节 02 G()=g+20,5+a (0<E<1) 延时环节 G(s)=e- 以上各式中：K为比例系数：T为时间常数：5为阻尼比：®为 无阻尼固有频率：x为延迟时间。 四、闭环系统的传递函数 闭环系统的传递函数方框图如图2.2.1所示。 0Go X,2 图2.2.1闭环系统的结构图 图中，前向通道的传递函数为 反馈通道的传递函数为 o-器 开环传递函数为 G.()=-G()H(s): E(s) 闭环传递函数为 G(s) G.o=X9-1±GoH可 X(s) 若H()=1,则此闭环系统为单位反馈系统。其闭环传递函数 为 请注意，这里所说的开环传递函数、反馈通道的传递函数和 前向通道的传递函数都只是一个闭环系统中一部分元件或环节

一阶惯性环节 1 1 ( ) + = Ts G s 积分环节 Ts G s 1 ( ) = 微分环节 G(s) = Ts 振荡环节 2 2 2 2 ( ) n n n s s G s ω ξ ω ω + + = （ 0 < ξ <1） 延时环节 s G s e −τ ( ) = 以上各式中： K 为 比 例 系 数 ；T 为时间常数；ξ 为阻尼比；ω n为 无阻尼固有频率； τ 为延迟时间。 四、闭环系统的传递函数 闭环系统的传递函数方框图如图 2.2.1 所示。 图 2.2.1 闭环系统的结构图 图中，前向通道的传递函数为 ( ) ( ) ( ) E s X s G s o = 反馈通道的传递函数为 ( ) ( ) ( ) X s B s H s o = 开环传递函数为 ( ) ( ) ( ) ( ) ( ) G s H s E s B s G s k = = ； 闭环传递函数为 1 ( ) ( ) ( ) ( ) ( ) ( ) G s H s G s X s X s G s i o B ± = = 。 若 ，则此闭环系统为单位反馈系统。其闭环传递函数 为 H (s) =1 1 ( ) ( ) ( ) ( ) ( ) G s G s X s X s G s i o B ± = = 。 请注意，这里所说的开环传递函数、 反馈通道的传递函数和 前向通道的传递函数都只是一个闭 环系统中一部分元件或环节

的传递函数，而闭环传递函数才是这个闭环系统的传递函数。表 示闭环系统内各种传递函数的符号只是一个符号而已，读者在遇 到相应的问题是，要根据各自的的概念作具体的分析。 2.3系统的传递函数方框图及其简化 一、传递函数方框图 在系统建模中，对于各个环节，分别用传递函数代表环节， 用环节输入、输出的Laplace变换代表其输入和输出，而形成的 一种表示系统与外界之间以及系统内部各变量之间的关系的方 框图就是传递函数方框图。与系统方框图相对应，它包含函数方 框、相加点和分支点等三种基本要素。 建立系统方框图的步骤如下： (1)建立系统（或元件）的原始微分方程： (2)对这些原始微分方程在初始状态为零的条件下进行 Laplace变换，并根据各个变换式的因果关系分别绘出相应的方 框图： (3)从系统的输入量与主反馈信号进行叠加的比较环节开 始，沿信号流动的方向，通过传递函数方框将所有的中间变量之 间的关系一一画出，直至画出系统的输出量与主反馈信号。 二、传递函数方框图等效的基本规则 传递函数方框图等效的基本规则如表2.3.1所示。 三、传递函数方框图简化的一般步骤 (1)确定系统的输入量和输出量，如果作用在系统的输入量有 多个，则必须分别对每一个输入量，逐个进行方框图的简化，求 得各自的传递函数。对于具有多个输出量的情况，也要分别进行 变换，求取各自的传递函数。 (2)若方框图中仅有多个无交叉回路，则按照先里后外的原 则，逐个简化，直至简化成一个方框的形式。若方框图中有交叉 的连接，用如下的方法

的 传 递 函 数 ，而 闭 环 传 递 函 数 才 是 这 个 闭 环 系 统 的 传 递 函 数 。表 示 闭 环 系 统 内 各 种 传 递 函 数 的 符 号 只 是 一 个 符 号 而 已 ，读 者 在 遇 到相应的问题是，要根据各自的的概念作具体的分析。 2.3 系统的传递函数方框图及其简化 一、传递函数方框图 在系统建模中，对于各个环节，分别用传递函数代表环节， 用环节输入、输出的 Laplace 变换代表其输入和输出，而形成的 一种表示系统与外界之间以及系统 内部各变量之间的关系的方 框 图 就 是 传 递 函 数 方 框 图 。与 系 统 方 框 图 相 对 应 ，它 包 含 函 数 方 框、相加点和分支点等三种基本要素。 建立系统方框图的步骤如下： (1)建立系统（或元件）的原始微分方程； (2) 对这些原始微分方程在初始状态为零的条件下进行 Laplace 变换，并根据各个变换式的因果关系分别绘出相应的方 框图； (3) 从系统的输入量与主反馈信号进 行叠加的比较环节开 始 ，沿 信 号 流 动 的 方 向 ，通 过 传 递 函 数 方 框 将 所 有 的 中 间 变 量 之 间的关系一一画出，直至画出系统的输出量与主反馈信号。 二 、 传 递 函 数 方 框 图 等 效 的 基 本 规 则 传递函数方框图等效的基本规则如表 2.3.1 所示。 三 、 传 递 函 数 方 框 图 简 化 的 一 般 步 骤 (1)确 定 系 统 的 输 入 量 和 输 出 量 ，如 果 作 用 在 系 统 的 输 入 量 有 多个，则必须分别对每一个输入量，逐个进行方框图的简化，求 得 各 自 的 传 递 函 数 。对 于 具 有 多 个 输 出 量 的 情 况 ，也 要 分 别 进 行 变换，求取各自的传递函数。 (2) 若方框图中仅有多个无交叉回路，则按照先里后外的原 则，逐个简化，直至简化成一个方框的形式。若方框图中有交叉 的连接，用如下的方法

方法一：若系统的传递函数方框图同时满足以下两个条件 条件1，整个系统方框图中只有一条前向通道： 条件2，各局部反馈回路间存在公共的传递函数方框。 则可以直接用下列公式求解： G0-81中之夏物是商面 前向通道的传递函数之积 （2.3.1) 括号内每一项的符号是这样决定的：在相加点处，对反馈信号为 相加时取负号，对反馈信号为相减时取正号 方法二：若系统的传递函数方框图不同时满足以上两个条件， 则可通过相加点、分支点的前后移动等法则，将系统传递函数方 框图化为同时满足以上两个条件的形式，然后应用公式（23.1) 即可。 方法三：若系统的传递函数方框图不同时满足以上两个条件， 可通过相加点、分支点的前后移动等法则，将交叉消除，简化成 无交叉的多回路形式。然后由里到外进行变换直至变换成一个单 回路或一个方框的形式，最后写出系统的传递函数。 在进行相加点或分支点前后移动时，应避免将相加点跨越分 支点或分支点跨越相加点，或将相加点和分支点的位置进行相互 交换，否则，方框图将更加复杂

方法一：若系统的传递函数方框图同时满足以下两个条件 条 件 1，整个系统方框图中只有一条前向通道； 条 件 2，各局部反馈回路间存在公共的传递函数方框。 则可以直接用下列公式求解： + ∑ = = ( ) 1 [ ] ( ) ( ) 每一反馈回路的开环传递函数 前向通道的传递函数之积 X s X s G s i o （ 2.3.1） 括号内每一项的符号是这样决定的：在相加点处，对反馈信号为 相加时取负号，对反馈信号为相减时取正号。 方法二： 若系统的传递函数方框图不同时满足以上两个条件， 则可通过相加点、分支点的前后移动等法则，将系统传递函数方 框图化为同时满足以上两个条件的形式，然后应用公式（ 2.3.1） 即可。 方法三：若系统的传递函数方框图不同时满足以上两个条件， 可通过相加点、分支点的前后移动等法则，将交叉消除，简化成 无交叉的多回路形式。然后由里到外进行变换直至变换成一个单 一回路或一个方框的形式，最后写出系统的传递函数。 在进行相加点或分支点前后移动时，应避免将相加点跨越分 支点或分支点跨越相加点，或将相加点和分支点的位置进行相互 交换，否则，方框图将更加复杂

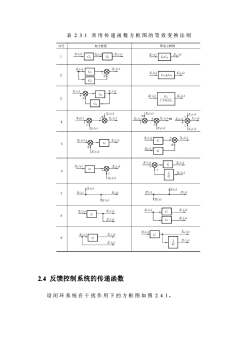
表2.3.1常用传递函数方框图的等效变换法则 序9 原方框衡 等效与框制 1 X Gh xi2 c.x Xa同X 2 唱9 X@±a9 3 8-回 ca☐ Xo 4 @-⑧ 8山 89@5号 X() “9⊙ 回-8@ @可 0o—⑧9 Gx. 同四 x() X⊙x型 回出 8起 回出 2.4反馈控制系统的传递函数 设闭环系统在干扰作用下的方框图如图2.4.1

表 2.3.1 常用传递函数方框图的等效变换法则 2.4 反馈控制系统的传递函数 设闭环系统在干扰作用下的方框图如图 2.4.1

8回态回￥ 回 图2.4.1闭环系统在干扰作用下的方框图 根据线性系统的叠加原理，系统输入与系统的干扰相互独立 地对系统起作用。 设输入X,(s)引起的输出为Xs),干扰N(9)引起的输出为Xx()。 令干扰N()为零，则可得系统在输入作用下的传递函数为 G,(s)G2(s) (2.4.1) 令输入X,(⑤)为零，则可得系统在干扰作用下的传递函数为 c-8o6w G(s) (2.4.2) 在上式中，若取G,(s)H(s>1,且G,(s)G,(s)Hs>1,则干扰所引 起的输出趋于0。因此，尽管系统在运行的过程中，干扰是不可 避免的，而对于反馈控制系统，只要系统参数选择适当，就可以 使系统具有很强的抗干扰能力。 从式(2.4.1)和式(2.4.2)可知，对于同一个闭环系统，当输入的 取法不同时，前向通道的传递函数不同，反馈回路的传递函数不 同，系统传递函数也不同，但传递函数的分母不变。这说明了系 统传递函数的分母确实反映了系统本身的固有特性，这个特性与 外界无关。而这一结论对开环系统并不适用。 相似系统（环节）：能用形式相同的数学模型来描述的物理系统 (环节)称为相似系统（环节）。 相似量：对于相似系统而言，在数学模型中占有相同位置的 物理量称为相似量。 系统传递函数或微分方程等数学模型表示的是系统的动态特 性，而与系统具体的物理构成无关。不同物理构成的相似系统可 以用相同形式的数学模型进行表示，它们具有相似的动态特性。 系统的相似性是进行系统模拟或系统仿真的基础

图 2.4.1 闭环系统在干扰作用下的方框图 根据线性系统的叠加原理，系统输入 与系统的干扰相互独立 地对系统起作用。 设输入 X i (s) 引起的输出为 X ox (s)，干 扰 N(s)引起的输出为 X oN (s)。 令干扰 N(s)为零，则可得系统在输入作用下的传递函数为 1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 2 1 2 G s G s H s G s G s X s X s G s i oX X + = = ( 2.4.1) 令输入 X i (s) 为零，则可得系统在干扰作用下的传递函数为 1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 2 2 G s G s H s G s N s X s G s oN N + = = ( 2.4.2) 在上式中，若取 G1 (s)H (s) >>1， 且 G1 (s)G2 (s)H (s) >>1，则干扰所引 起的输出趋于 0。 因此， 尽管系统在运行的过程中， 干扰是不可 避免的，而对于反馈控制系统，只要系统参数选择适当，就可以 使系统具有很强的抗干扰能力。 从 式 (2.4.1)和 式 (2.4.2)可知，对于同一个闭环系统，当输入的 取法不同时，前向通道的传递函数不同，反馈回路的传递函数不 同 ，系统传递函数也不同，但传递函数的分母不变。这说明了系 统传递函数的分母确实反映了系统本身的固有特性，这个特性与 外界无关。而这一结论对开环系统并不适用。 相似系统 (环 节 )：能用形式相同的数学模型来描述的物理系统 (环 节 )称为相似系统 (环 节 )。 相似量：对于相似系统而言，在数学 模型中占有相同位置的 物理量称为相似量。 系统传递函数或微分方程等数学模型 表示的是系统的动态特 性 ，而与系统具体的物理构成无关。不同物理构成的相似系统可 以用相同形式的数学模型进行表示，它们具有相似的动态特性。 系统的相似性是进行系统模拟或系统仿真的基础

基本要求、重点和难点 一、基本要求 ()了解数学模型的基本概念。能够运用动力学、电学及专 业知识，列写机械系统、电子网络的微分方程 (2)掌握传递函数的概念、特点，会求传递函数的零点、极 点及放大系数。 (3)能够用分析法求系统的传递函数。 (4)掌握各个典型环节的特点，传递函数的基本形式及相关 参数的物理意义。 (5)了解传递函数方框图的组成及意义：能够根据系统微分 方程，绘制系统传递函数方框图，并实现简化，从而求出系统传 递函数。 (6)掌握闭环系统中前向通道传递函数、开环传递函数、闭 环传递函数的定义及求法。掌握干扰作用下，系统的输出及传递 函数的求法和特点。 (7)了解相似原理的概念。 (8)了解系统的状态空间表示法，了解MATLAB中，数学模 型的几种表示法。 二、本章重点 (1)系统微分方程的列写。 (2)传递函数的概念、特点及求法；典型环节的传递函数。 (3)传递函数方框图的绘制及简化。 三、本章难点 (1)系统微分方程的列写。 (2)传递函数方框图的绘制及简化。 例题 例2.1设有一个倒摆装在只能沿x方向移动的小车上，如图

基本要求、重点和难点 一、 基本要求 (1)了解数学模型的基本概念。能够 运用动力学、电学及专 业知识，列写机械系统、电子网络的微分方程。 (2)掌握传递函数的概念、特点，会 求传递函数的零点、极 点及放大系数。 (3)能够用分析法求系统的传递函数。 (4)掌握各个典型环节的特点，传递 函数的基本形式及相关 参数的物理意义。 (5)了解传递函数方框图的组成及意 义；能够根据系统微分 方程，绘制系统传递函数方框图，并实现简化，从而求出系统传 递函数。 (6)掌握闭环系统中前向通道传递函 数、开环传递函数、闭 环传递函数的定义及求法。掌握干扰作用下，系统的输出及传递 函数的求法和特点。 (7)了解相似原理的概念。 (8)了解系统的状态空间表示法，了解 MATLAB 中，数学模 型的几种表示法。 二、本章重点 (1)系统微分方程的列写。 (2)传递函数的概念、特点及求法；典型环节的传递函数。 (3)传递函数方框图的绘制及简化。 三、本章难点 (1)系统微分方程的列写。 (2)传递函数方框图的绘制及简化。 例题 例 2.1 设有一个倒摆装在只能沿 x 方向移动的小车上， 如 图