《机械工程控制基础》课程教学资源（讲稿）第五章 系统的稳定性

第五章系统的稳定性 讲授内容 5.1系统稳定的初步概念 一、稳定性的定义 系统稳定性是指系统在干扰作用下偏离平衡位置，当干扰撒 除后，系统自动回到平衡位置的能力。 若系统在初始状态的影响下，由它所引起的系统的时间响应 随着时间的推移，逐渐衰减并趋向于零（即回到平衡位置），则 称系统为稳定的；反之，由它所引起的系统的时间响应随着时间 的推移而发散（即偏离平衡位置越来越远），则称系统为不稳定 的。 线性系统的稳定性是系统的固有特性，仅与系统的结构及参 数有关：而非线性系统的稳定性不仅与系统的结构及参数有关， 而且还与系统的输入有关。 二、系统稳定的充要条件 系统稳定的充要条件是的系统所有特征根的实部全都小于 零，或系统传递函数的所有极点均分布在5平面的左半平面内。 若系统传递函数的所有极点中，只有一个位于虚轴上，而其 它极点均分布在s平面的左半平面内，则系统临界稳定。而临界 稳定的系统极易因为系统的结构或参数的细微变化而变成不稳 定的系统。因此，临界稳定往往也归结为不稳定的一种

第五章 系统的稳定性 讲授内容 5.1 系统稳定的初步概念 一、稳定性的定义 系统稳定性是指系统在干扰作用下偏离平衡位置，当干扰撤 除后，系统自动回到平衡位置的能力。 若系统在初始状态的影响下，由它所引起的系统的时间响应 随着时间的推移，逐渐衰减并趋向于零（即回到平衡位置）， 则 称 系 统 为 稳 定 的 ；反 之 ，由 它 所 引 起 的 系 统 的 时 间 响 应 随 着 时 间 的 推 移 而 发 散 （ 即 偏 离 平 衡 位 置 越 来 越 远 ）， 则 称 系 统 为 不 稳 定 的 。 线性系统的稳定性是系统的固有特性，仅与系统的结构及参 数有关；而非线性系统的稳定性不仅与系统的结构及参数有关， 而且还与系统的输入有关。 二、系统稳定的充要条件 系统稳定的充要条件是的系统所有特征根的实部全都小于 零，或系统传递函数的所有极点均分布在 s 平面的左半平面内。 若系统传递函数的所有极点中，只有一个位于虚轴上，而其 它极点均分布在 s 平面的左半平面内，则系统临界稳定。而临界 稳定的系统极易因为系统的结构或 参数的细微变化而变成不稳 定的系统。因此，临界稳定往往也归结为不稳定的一种

5.2Rouh（劳斯)稳定判据 Roh判据是判别系统特征根分布的一个代数判据。 一、系统稳定的必要条件 要使系统稳定，即系统全部特征根均具有负实部，就必须满 足以下两个条件： 1)特征方程的各项系数都不等于零。 2)特征方程的各项系数的符号都相同。 此即系统稳定的必要条件。 按习惯，一般取最高阶次项的系数为正，上述两个条件可以 归结为一个必要条件，即系统特征方程的各项系数全大于零，且 不能为零 二、系统稳定的充要条件 系统稳定的充要条件是Rouh表的第一列元素全部大于零，且 不能等于零。 运用Roh判据还可以判定一个不稳定系统所包含的具有正 实部的特征根的个数为Rouh表第一列元素中符号改变的次数。 运用Rouh判据的关键在于建立Roh表。建立Rouh表的方法 请参阅相关的例题或教材。运用Rouh判据判定系统的稳定性， 需要知道系统闭环传递函数或系统的特征方程。 在应用Roh判据还应注意以下两种特殊的情况： 1.如果在Rouh表中任意一行的第一个元素为0，而其后各元不 全为0，则在计算下一行的第一个元时，该元将趋于无穷大。于 是Roh表的计算无法继续。为了克服这一困难，可以用一个很 小的正数s代替第一列等于0的元素，然后计算Roh表的其余各 元。若￡上下各元符号不变，切第一列元素符号均为正，则系统 特征根中存在共轭的虚根。此时，系统为临界稳定系统

5.2 Routh（劳斯）稳定判据 Routh 判据是判别系统特征根分布的一个代数判据。 一、系统稳定的必要条件 要使系统稳定， 即系统全部特征根均具有负实部， 就必须满 足以下两个条件： 1）特征方程的各项系数都不等于零。 2）特征方程的各项系数的符号都相同。 此即系统稳定的必要条件。 按习惯， 一般取最高阶次项的系数为正， 上述两个条件可以 归结为一个必要条件，即系统特征方程的各项系数全大于零，且 不能为零。 二、系统稳定的充要条件 系统稳定的充要条件是 表的第一列元素全部大于零，且 不能等于零。 Routh 运 用 判据还可以判定一个不稳定系统所包含的具有正 实部的特征根的个数为 表第一列元素中符号改变的次数。 Routh Routh 运 用 判据的关键在于建立 表。建立 表的方法 请参阅相关的例题或教材。运用 判据判定系统的稳定性， 需要知道系统闭环传递函数或系统的特征方程。 Routh Routh Routh Routh 在应用 Routh 判据还应注意以下两种特殊的情况： 1．如果在 表中任意一行的第一个元素为 0，而其后各元不 全 为 0， 则在计算下一行的第一个元时， 该元将趋于无穷大。 于 是 表的计算无法继续。为了克服这一 困难，可以用一个很 小的正数 Routh Routh ε 代替第一列等于 0 的元素，然后计算 表的其余各 元。若 Routh ε 上下各元符号不变，切第一列元素符号均为正，则系统 特征根中存在共轭的虚根。此时，系统为临界稳定系统

2.如果在Routh表中任意一行的所有元素均为0，Rouh表的计算 无法继续。此时，可以利用该行的上一行的元构成一个辅助多项 式，并用多项式方程的导数的系数组成Roh表的下一行。这样 Roh表中的其余各元就可以计算下去。出现上述情况，一般是 由于系统的特征根中，或存在两个符号相反的实根（系统自由响 应发散，系统不稳定)，或存在一对共轭复根（系统自由响应发 散，系统不稳定)，或存在一对共轭的纯虚根（即系统自由响应 会维持某一频率的等幅振荡，此时，系统临界稳定)，或是以上 几种根的组合等。这些特殊的使系统不稳定或临界稳定的特征根 可以通过求解辅助多项式方程得到。 三、相对稳定性的检验 对于稳定的系统，运用Rouh判据还可以检验系统的相对稳 定性，采用以下方法： 1)将s平面的虚轴向左移动某个数值，即令s=zσ（σ为正实数）， 代入系统特征方程，则得到关于z的特征方程。 2)利用Roh判据对新的特征方程进行稳定性判别。如新系统稳 定，则说明原系统特征方程所有的根均在新虚轴之左边，。越大， 系统相对稳定性越好。 5.3 Nyquis1（乃奎斯特)稳定判据 一、辅助函数及其与开环、闭环传递函数零点和极点的关系 如图5.3.1所示的闭环系统，其闭环传递函数为 G(s) G,)=1+G)H() (5.3.1) 开环传递函数为：

2．如果在 表中任意一行的所有元素均为 0， 表的计算 无法继续。此时，可以利用该行的上一行的元构成一个辅助多项 式 ， 并用多项式方程的导数的系数组成 表的下一行。 这样， 表中的其余各元就可以计算下去。出 现上述情况，一般是 由于系统的特征根中，或存在两个符号相反的实根（系统自由响 应发散，系统不稳定），或存在一对共轭复根（系统自由响应发 散，系统不稳定），或存在一对共轭的纯虚根（即系统自由响应 会维持某一频率的等幅振荡，此时，系统临界稳定），或是以上 几种根的组合等。这些特殊的使系统不稳定或临界稳定的特征根 可以通过求解辅助多项式方程得到。 Routh Routh Routh Routh 三、相对稳定性的检验 对于稳定的系统，运用 判据还可以检验系统的相对稳 定性，采用以下方法： Routh 1）将 s 平面的虚轴向左移动某个数值，即 令 s=z-σ (σ 为正实数）， 代入系统特征方程，则得到关于 z 的特征方程。 2） 利 用 判据对新的特征方程进行稳定性判别。 如新系统稳 定 ，则说明原系统特征方程所有的根均在新虚轴之左边，σ 越大， 系统相对稳定性越好。 Routh 5.3 Nyquist （乃奎斯特）稳定判据 一、辅助函数及其与开环、闭环传递函数零点和极点的关系 如 图 5.3.1 所示的闭环系统，其闭环传递函数为 1 ( ) ( ) ( ) ( ) G s H s G s G s B + = ； (5.3.1） 开环传递函数为：

Gx(s)=G(s)H(s): 令F(s)=1+Gs)Hs), (5.3.2) 图5.3.1 则G(s)、F(s)、Gx(s)三者的零点和极点之间存在如下关系： F(s)的零点与Ga(s)的极点重合：F(s)的极点与Gx(s)的极点重 合。 因此，系统稳定的充要条件由原来的G(s)的全部极点均位于 s平面的左半平面内，变成为F()的全部零点均位于s平面的左 半平面内，或F(s)在s平面的右半平面内无零点。 二、幅角原理 设F()函数在s平面上（除有限个奇点外）为单值的连续正则 函数。并设s平面上解析点s映射到F(s)平面上为点F(s),或为 原点指向此映射点的向量F(s)。若在s平面上任意选定一封闭曲 线L,只要此曲线不经过F(s)的奇点，就可将s平面上的封闭曲 线L,映射到F(s)平面上去，结果也是一条封闭曲线，记为Le。当 解析点s按顺时针方向沿L变化一周时，向量F(s)将按顺时针方 向旋转N周，即曲线L顺时针包围原点N次。若令：Z为包围于 L,内F(s)函数的零点数：P为包围于L,内F(s)函数的极点数，则存 N=Z-P (5.3.3) 其中，N>0,表示L顺时针包围原点N次： N<0,表示L=逆时针包围原点N次： N=0,表示L不包围原点

G (s) G(s)H(s) K = ； 令 F(s) = 1+ G(s)H(s)， （ 5.3.2） 图 5.3.1 则 GB (s)、 F(s)、 GK (s)三者的零点和极点之间存在如下关系： F(s)的零点与 的极点重合； 的极点与 的极点重 合 。 G (s) B F(s) G (s) K 因此，系统稳定的充要条件由原来的 的全部极点均位于 s 平面的左半平面内，变成为 的全部零点均位于 s 平面的左 半平面内，或 在 s 平面的右半平面内无零点。 G (s) B F(s) F(s) 二、幅角原理 设 函数在 s 平面上（除有限个奇点外）为单值的连续正则 函数。并设 s 平面上解析点 s 映射到 平面上为点 ，或为 原点指向此映射点的向量 。若在 s 平面上任意选定一封闭曲 线 ，只要此曲线不经过 的奇点，就可将 s 平面上的封闭曲 线 映射到 平面上去， 结果也是一条封闭曲线， 记 为 。 当 解析点 s 按顺时针方向沿 变化一周时，向量 将按顺时针方 向旋转 周 ， 即曲线 顺时针包围原点 次 。 若令： F(s) F(s) F(s) F(s) Ls F(s) Ls F(s) LF Ls F(s) N LF N Z 为包围于 Ls 内 F(s)函数的零点数；P 为包围于 内 函数的极点数，则 存 在 Ls F(s) N = Z − P （ 5.3.3） 其中， N >0,表 示 LF 顺时针包围原点 N 次 ； N <0, 表 示 LF 逆时针包围原点 N 次 ； N =0, 表 示 LF 不包围原点

根据式(5.3.3)有：Z=N+P。其中，N为L顺时针包围原 点的次数：P为F(s)包围于L,的极点数，亦即为G(s)包围于L,的 极点数：Z为包围于L,内的F(s)函数的零点数，亦即为G(s)包围 于L的极点数。 三、s平面封闭曲线的选取 要想判定系统是否稳定，只需合理选择5平面封闭曲线L, 判定该封闭曲线内是否包围F(s)的零点即可。根据系统稳定的条 件，若选取封闭曲线L,使其顺时针包围整个s平面的右半平面， 此时，若Z=0,则系统稳定：反之，系统不稳定。因此，封闭曲 线L,可以这样由以下两段组成：①整个虚轴（即o从-∞变化到 +∞)，②以原点为圆心，无穷大为半径的半圆弧。 四、F(s)、Gx(s)轨迹的关系 由式(5.3.2)有：Gx(s)=F(s)-1 即有Gx(s)的轨迹实质上是F(s)轨迹在实轴方向上左移一个 单位得到的。因此，F(s)绕原点旋转的圈数实质上是Gx(s)绕(-l,0) 旋转的圈数。这样一来，可以用Gx(s)的轨迹绕(~L0)旋转的圈数 代替F(s)的轨迹绕原点旋转的圈数N。 五、Gx(s)轨迹 Gx(s)轨迹由两部分组成： 一部分是s沿着整个虚轴移动，即s=j0且0从-0变化到+o

根据式（ 5.3.3）有： Z = N + P 。其中， 为 顺时针包围原 点的次数； N LF P 为 包围于 的极点数，亦即为 包围于 的 极点数； F(s) Ls G (s) K Ls Z 为包围于 内 的 函数的零点数，亦即为 包 围 于 的极点数。 Ls F(s) G (s) B Ls 三、s 平面封闭曲线的选取 要想判定系统是否稳定，只需合理选择 s 平面封闭曲线 ， 判定该封闭曲线内是否包围 的零点即可。 根据系统稳定的条 件 ，若选取封闭曲线 ，使其顺时针包围整个 s 平面的右半平面， 此时， 若 Ls F(s) Ls Z = 0， 则系统稳定； 反之， 系统不稳定。 因此， 封闭曲 线 Ls 可以这样由以下两段组成：①整个虚轴（即 ω 从 变化到 ），②以原点为圆心，无穷大为半径的半圆弧。 − ∞ + ∞ 四、F(s)、GK (s)轨迹的关系 由式（ 5.3.2）有： G (s)= -1 K F(s) 即 有 的轨迹实质上是 轨迹在实轴方向上左移一个 单位得到的。因 此 ， 绕原点旋转的圈数实质上是 绕 旋转的圈数。这样一来，可以用 的轨迹绕 G (s) K F(s) F(s) G (s) K (−1, j0) G (s) K (−1, j0)旋转的圈数 代 替 F(s)的轨迹绕原点旋转的圈数 N 。 五、GK (s)轨迹 G (s) K 轨迹由两部分组成： 一部分是 s 沿着整个虚轴移动，即 s = jω 且 ω 从 − ∞变化到 + ∞

时Gx(s)的轨迹。此时，Gx(s)的轨迹就是GkUo)的Nyquist轨迹，且 0从-o变化到+0。 另一部分是$沿着无穷大半圆的圆弧顺时针运动，此时 →∞，Gx(s)的轨迹为原点或某一定点。而这点显然不会影响整 个Gx(s)的轨迹顺时针包围(~10)点的圈数。因此，可以不予表示 因此，G(s)的轨迹可以简单地认为就是G(U)在o从-∞变化 到+o时的quist轨迹。可以证明，Gx(jo)在o从-o变化到0时的 Nyquist轨迹与Gx(Uo)在o从0变化到+o时的Nyquist轨迹是关于实 轴对称的，因此，作出Gx(jo)在o从0变化到+o时的Nyquist轨迹 后，就可以得到GxUo)在o从-o变化到0时的Nyquist轨迹。 在作Gx(Uo)在o从-o变化到+o时的quis轨迹时，要注意当 系统开环存在积分环节时，Go)在)从-∞变化到+0时的 qis1轨迹就会出现间断点。若v型开环系统属于最小相位系统 间断点处的轨迹可以通过以下法则连接：当s沿着小半圆从。=0 变化到。=0时，Mg轨迹将沿无穷大半径按顺时针方向从，子 转到受 六、Nyquist判据 设G(s)位于s平面的右半平面的极点数为P,GxUo)的Nyquis1 轨迹(0从-o变化到+)顺时针包围(-L,0)的圈数为N,则系 统稳定的充要条件是：N=-P。 Nqis判据可以根据系统开环频率特性的Nyquist图，判定闭环 系统的稳定性。事实上，其作用还在于应用该判据能很容易分析

时 GK (s)的轨迹。此时， GK (s)的轨迹就是 G ( jω) K 的 Nyquist 轨迹，且 ω 从 − ∞变化到 + ∞ 。 另一部分是 s 沿着无穷大半圆的圆弧顺时针运动，此时 s → ∞ ， 的轨迹为原点或某一定点。 而这点显然不会影响整 个 的轨迹顺时针包围 G (s) K G (s) K (−1, j0)点的圈数。因此，可以不予表示。 因 此 ，GK (s)的轨迹可以简单地认为就是 G ( jω) K 在 ω 从 变 化 到 时 的 轨迹。可以证明， − ∞ + ∞ Nyquist G ( jω) K 在 ω 从 − ∞变化到 0 时 的 Nyquist 轨迹与 G ( jω) K 在 ω 从 0 变化到 + ∞ 时 的 轨迹是关于实 轴对称的，因此，作出 Nyquist G ( jω) K 在 ω 从 0 变化到 + ∞ 时 的 轨 迹 后，就可以得到 Nyquist G ( jω) K 在 ω 从 − ∞变化到 0 时 的 Nyquist 轨迹。 在 作 G ( jω) K 在 ω 从 − ∞变化到 + ∞ 时 的 轨迹时，要注意当 系统开环存在积分环节时， Nyquist G ( jω) K 在 ω 从 − ∞ 变化到 时 的 轨迹就会出现间断点。若 型开环系统属于最小相位系统， 间断点处的轨迹可以通过以下法则连接：当 s 沿着小半圆从 变化到 时 ， 轨迹将沿无穷大半径按顺时针方向从 + ∞ Nyquist v − ω = 0 + ω = 0 Nyquist 2 π v 转 到 2 π − v 。 六、 Nyquist 判据 设 GK (s)位 于 s 平面的右半平面的极点数为 P ，G ( jω) K 的 轨迹（ Nyquist ω 从 − ∞ 变化到 + ∞ ）顺时针包围 (−1, j0) 的圈数为 ，则系 统稳定的充要条件是： N N = −P。 Nyquist 判据可以根据系统开环频率特性的 图 ，判定闭环 系统的稳定性。事实上，其作用还在于应用该判据能很容易分析 Nyquist

系统的结构与参数对系统稳定性的影响。 在利用Nyquist判据判定系统的稳定性时，要注意N、P、Z的 具体含义。 5.4Bode(伯德)稳定判据 一、Bode图与Nyquist图的对应关系 如图5.4.1所示，Bode图与Mgui图之间存在如下对应关系 1.极坐标图上的单位圆相当于Bode图上的0分贝线，即对数幅 频特性图的横坐标轴。 2.极坐标图上的负实轴线相当于Bod图上的-180°线，即对数相 频特性图的横坐标轴。 图中，o.为Nqui轨迹与单位圆交点处的频率，即对数幅频 特性曲线与横轴交点的频率，亦即输入与输出幅值相等时的频率 (开环输入与输出的量纲相同)，称为剪切频率或幅值穿越频率、 幅值交界频率： o.为Nyquis1轨迹与负实轴交点的频率，即对数相频特性曲线 与横轴交点的频率，称为相位穿越频率或相位交界频率。 20lg GH 图5.4.1

系统的结构与参数对系统稳定性的影响。 在利用 Nyquist 判据判定系统的稳定性时， 要注意 N 、 P 、 Z 的 具体含义。 5.4 Bode(伯德)稳定判据 一、Bode图与 Nyquist 图的对应关系 如 图 5.4.1 所示， Bode 图 与 Nyquist 图之间存在如下对应关系： 1．极坐标图上的单位圆相当于 图上的 0 分贝线，即对数幅 频特性图的横坐标轴。 Bode 2．极坐标图上的负实轴线相当于 Bode 图上的 -180 o 线，即对数相 频特性图的横坐标轴。 图中， ωc 为 轨迹与单位圆交点处的频率，即对数幅频 特性曲线与横轴交点的频率，亦即输入与输出幅值相等时的频率 （开环输入与输出的量纲相同），称为剪切频率或幅值穿越频率、 幅值交界频率； Nyquist ω g 为 轨迹与负实轴交点的频率 ，即对数相频特性曲线 与横轴交点的频率，称为相位穿越频率或相位交界频率。 Nyquist 图 5.4.1

二、穿越的概念 开环频率特性Mgui1轨迹在(-L,0)点以左穿越负实轴称为 “穿越”。若沿频率o增加的方向，开环qi1轨迹自上而下穿越 (-1,0)以左的负实轴称为正穿越；反之，称为负穿越。若沿频率。 增加的方向，开环Mgir轨迹自(-l,0)以左的负实轴开始向下称 为半次正穿越：反之，若沿频率o增加的方向，开环Nyquist轨迹 自(-1,0)以左的负实轴开始向上称为半次负穿越。 对应于Bod图上，在开环对数幅频特性为正值的频率范围 内，沿增加的方向，对数相频特性曲线自下而上穿越-180°线为 正穿越；反之，称为负穿越。若对数相频特性曲线自-180°线开 始向上，称为半次正穿越：反之，若对数相频特性曲线自-180°线 开始向下，称为半次负穿越。 三、Bode判据 设系统开环传递函数在[s]平面的右半平面的极点数为P,则 对应的闭环系统稳定性判据是：在Bode图上，当o由0变到+∞ 时，在开环对数幅频特性为正值的频率范围内，开环对数相频特 性对-180°线正穿越的次数与负穿越的次数之差为P以时，闭环系 统稳定：否则，闭环系统不稳定。 当系统开环稳定(P=0)时，若开环对数幅频特性比其对数 相频特性先交于横轴，即0。<®，则闭环系统稳定；若开环对数 相频特性比其对数幅频特性先交于横轴，即®。<⊙。，则闭环系统 不稳定：若0。=0。，则闭环系统临界稳定。 若开环对数幅频特性对横轴有多个剪切频率，则取最大的那 个来判定系统的稳定性

二、穿越的概念 开环频率特性 Nyquist 轨迹在 (−1, j0) 点以左穿越负实轴称为 “穿越”。若沿频率 ω 增加的方向，开 环 轨迹自上而下穿越 以左的负实轴称为正穿越；反之，称为负穿越。若沿频率 Nyquist (−1, j0) ω 增加的方向，开环 Nyquist 轨迹自 (−1, j0) 以左的负实轴开始向下 称 为半次正穿越；反之，若沿频率 ω 增加的方向，开环 轨 迹 自 以左的负实轴开始向上称为半次负穿越。 Nyquist (−1, j0) 对应于 图上，在开环对数幅频特性为正值的频率范围 内 ，沿 Bode ω 增加的方向，对数相频特性曲线自下而上穿越 -180 o线 为 正穿越；反之，称为负穿越。若对数相频特性曲线自 - 18 0o线 开 始向上，称为半次正穿越；反之，若对数相频特性曲线自 -180 o线 开始向下，称为半次负穿越。 三、Bode判据 设系统开环传递函数在 [s]平面的右半平面的极点数为 P ，则 对应的闭环系统稳定性判据是：在 Bode 图上，当 ω 由 0 变 到 + ∞ 时 ，在开环对数幅频特性为正值的频率范围内，开环对数相频特 性 对 −180°线正穿越的次数与负穿越的次数之差为 2 P 时，闭环系 统稳定；否则，闭环系统不稳定。 当系统开环稳定（ P = 0）时，若开环对数幅频特性比其 对 数 相频特性先交于横轴， 即 ωc < ω g ， 则闭环系统稳定； 若开环对数 相频特性比其对数幅频特性先交于横轴，即 ω g < ωc ，则闭环系统 不稳定；若 ω g = ωc ，则闭环系统临界稳定。 若开环对数幅频特性对横轴有多个剪 切频率，则取最大的那 个来判定系统的稳定性

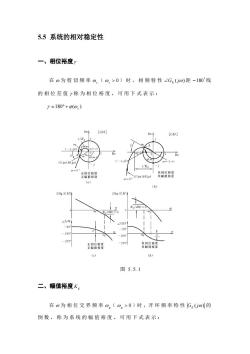
5.5系统的相对稳定性 一、相位裕度) 在o为剪切频率o。（0。>0)时，相频特性∠GxUo)距-180'线 的相位差值y称为相位裕度。可用下式表示： y=180°+p(o.) [GH] GH (e) 图5.5.1 二、幅值裕度K 在o为相位交界频率0。(0，>0)时，开环频率特性Gxo的 倒数，称为系统的幅值裕度。可用下式表示：

5.5 系统的相对稳定性 一、相位裕度γ 在 ω 为剪切频率 ωc（ ωc > 0 ） 时 ， 相频特性 G ( jω) ∠ K 距 线 的相位差值 ° −180 γ 称为相位裕度。可用下式表示： 180 ( ) ϕ ωc γ = ° + 图 5.5.1 二、幅值裕度Kg 在 ω 为相位交界频率 ω g（ ω g > 0 ）时 ，开环频率特性 G ( jω) K 的 倒数，称为系统的幅值裕度。可用下式表示：

K:-G Go. 在Bode图上，幅值裕度改以分贝表示为： 20lgK,=2018G (jo, -201gGx(J@,)AK.(dB). 因此，系统稳定的充要条件还可表述为：幅值裕度K。、相位 裕度y均大于零。 幅值裕度K。、相位裕度y在Nyquist图和Bode图上的表示如 图5.5.1所示。 基本要求、重点和难点 一、基本要求 1,了解系统稳定性的定义、系统稳定的条件： 2.掌握Rouh判据的必要条件和充要条件，学会应用Rouh判据判 定系统是否稳定，对于不稳定系统，能够指出系统包含不稳定的 特征根的个数： 3.掌握Nyquist判剧： 4,理解Nyquist图和Bode图之间的关系： 5.掌握Bode判剧： 6.理解系统相对稳定性的概念，会求相位裕度和幅值裕度，并 能够在Nyquist图和Bode图上加以表示。 二、本章重点 I.Routh判剧、Nyquist判剧和Bode判剧的应用： 2,系统相对稳定性；相位裕度和幅值裕度求法及其在Nyquist 图和Bode图的表示法

( ) 1 K g g G j K ω = 在 Bode 图上，幅值裕度改以分贝表示为： 20lg ( ) ( ). ( ) 1 20lg 20lg G j K dB G j K K g g K g g = = − ω ∆ ω 因此，系统稳定的充要条件还可表述为：幅值裕度 、相 位 裕 度 Kg γ 均大于零。 幅值裕度 Kg 、相位裕度 γ 在 Nyq uist 图 和 Bode 图上的表示如 图 5.5.1 所示。 基本要求、重点和难点 一、基本要求 1．了解系统稳定性的定义、系统稳定的条件； 2．掌 握 判据的必要条件和充要条件，学会应用 判据判 定系统是否稳定，对于不稳定系统，能够指出系统包含不稳定的 特征根的个数； Routh Routh 3．掌握 Nyquist 判剧； 4．理解 Nyquist 图 和 Bode 图之间的关系； 5．掌握 Bode 判剧； 6．理解系统相对稳定性的概念，会 求相位裕度和幅值裕度，并 能够在 Nyquist 图 和 Bode 图上加以表示。 二、本章重点 1． Routh 判剧、 Nyquist 判剧和 Bode 判剧的应用； 2．系统相对稳定性；相位裕度和幅 值裕度求法及其在 Nyquist 图 和 Bode 图的表示法