《机械工程控制基础》课程教学资源（讲稿）第三章 时间响应分析

第三章时间响应分析 讲授内容 3.1时间响应及其组成 一、时间响应 时间响应是指系统的响应（输出）在时域上的表现形式，或 系统的动力学方程在一定初始条件下的解。 二、时间响应的组成 对于一个n阶线性定常系统，输入x,)与输出x,)之间关系的微 分方程 ax。00+an-lx。"-(0+.+a)+ax.0） =6.“0+b0++60+6x0 (n2m) 设其特征根为s=12,),则系统的时间响应可表示成 x0=0+立A,e”+24,e” (3.1.1) 按响应的来源分为零状态响应和零输入响应。其中，零状态 响应是指初始状态为零时，由系统的输入引起的响应，即 B0+立A,”:零输入响应是指系统的输入为零时，由初始状态引 起的响应，即A”。在控制工程中，如无特别声明，所讲的响 应往往是零状态响应。 时间响应还可按其性质分为强迫响应项)，自由响应项

第三章 时间响应分析 讲授内容 3.1 时间响应及其组成 一、时间响应 时间响应是指系统的响应（输出）在 时域上的表现形式，或 系统的动力学方程在一定初始条件下的解。 二、时间响应的组成 对于一个 n阶线性定常系统，输 入 与输出 之间关系的微 分方程 x (t) i x (t) o ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 0 ( 1) 1 ( ) 1 0 ( 1) 1 ( ) b x t b x t b x t b x t a x t a x t a x t a x t i i m m i m m i o o n n o n n o = + + + + + + + + − − − − L & L & (n ≥ m) 设其特征根为 si (i =1,2,L, n)，则系统的时间响应可表示成 ∑ ∑ = = = + + n i s t i n i s t o i i i x t B t A e A e 1 2 1 1 ( ) ( ) （ 3.1.1） 按响应的来源分为零状态响应和零输入响应。其中，零状态 响应是指初始状态为零时，由系统的输入引起的响应，即 ； 零输入响应是指系统的输入为零时， 由初始状态引 起的响应， 即 ∑ 。 在 控制工程中， 如无特别声明， 所讲的响 应往往是零状态响应。 ∑= + n i s t i i B t A e 1 1 ( ) = n i s t i i A e 1 2 时间响应还可按其性质分为强迫响应项 B(t) ，自由响应项

空ev空uew 三、微分方程特征根的意义 由式(3.1.1)可知，若系统的所有特征根s=12,.,m)均具有负 实部，即Rs,0,则有其 自由响应项4，”+∑4，e“最终会趋于无穷大，即系统的自由响应 项发散。这种系统称为不稳定系统。若系统有一个特征根的实部 为0，而其余特征根的实部均为负数，则其自由响应项 立4，e”+立4，e"最终会变成一等幅振荡，这种系统称为临界稳定系 统。 因此，系统特征根的实部决定了系统的稳定与否。若系统特 征根的实部全部都小于零，则系统稳定：若系统特征根的实部不 全小于零，则系统不稳定。由系统特征根与系统传递函数极点之 间的对应关系，还可得系统稳定的另一判据：若系统传递函数的 所有极点均分布在[$]平面的左半平面内，则系统稳定：若系统传 递函数在[s]平面的右半平面内存在极点，则系统不稳定。 对于稳定系统，Rs,]绝对值的大小决定了它所对应的自由响 应项衰减的快慢。Rs,]绝对值越大，则它所对应的的自由响应项 衰减得越快；反之亦然。而系统特征根的虚部ms,]的分布情况在 很大程度上决定了系统自由响应的振荡情况，绝对值越大，则自 由响应项振荡频率越高，它决定了系统的响应在规定时间内接近 稳态响应的情况，这影响着系统响应的准确性

∑ ∑ = = + n i s t i n i s t i i i A e A e 1 2 1 1 。 三、微分方程特征根的意义 由 式（ 3.1.1）可知，若系统的所有特征根 s (i 1,2, , n) i = L 均具有负 实部，即 Re[si ] 0 ∑ ∑ = = + n i s t i n i s t i i i A e A e 1 2 1 1 ∑ ∑ = = + n i s t i n i s t i i i A e A e 1 2 1 1 因此，系统特征根的实部决定了系统 的稳定与否。若系统特 征根的实部全部都小于零，则系统稳定；若系统特征根的实部不 全小于零，则系统不稳定。由系统特征根与系统传递函数极点之 间的对应关系，还可得系统稳定的另一判据：若系统传递函数的 所有极点均分布在 [s]平面的左半平面内，则系统稳定；若系统传 递函数在 [s]平面的右半平面内存在极点，则系统不稳定。 对于稳定系统， 绝对值的大小决定了它所对应的自由响 应项衰减的快慢。 绝对值越大，则它所对应的的自由响应项 衰减得越快；反之亦然。而系统特征根的虚部 的分布情况在 很大程度上决定了系统自由响应的振荡情况，绝对值越大，则 自 由响应项振荡频率越高，它决定了系统的响应在规定时间内接近 稳态响应的情况，这影响着系统响应的准确性。 Re[ ]i s Re[ ]i s Im[ ]i s

3.2典型输入信号 在控制工程中，常用的输入信号有两大类。其一是系统正常 工作时的输入信号：其二是外加的测试信号，包括单位脉冲信号 单位阶跃信号、单位斜坡信号、正弦信号和某些随机信号等。输 入信号的选择要综合考虑系统的工作条件和实验的目的。 3.3一阶系统的时间响应 一、一阶系统 一阶系统传递函数的一般形式为 C 式中，T称为一阶系统的时间常数，K称为一阶系统的增益。 二、一阶系统的单位脉冲响应) 0=rxo=rK6o1=1-s立 (120) )只有瞬态项，而其稳态项为零。即一阶系统的单位脉冲 响应函数是一个递减的指数函数。 对一阶系统而言，将其单位脉冲响应曲线衰减到初值的2%之 前的过程定义为过渡过程，称此过程经历的时间为过渡过程时间 或调整时间，记为1，。经过计算可得一阶系统的调整时间为4T。 显然，系统的时间常数T愈小，其过渡过程的持续时间愈短，亦 即系统的惯性愈小，系统对输入信号反应的快速性愈好

3.2 典型输入信号 在控制工程中，常用的输入信号有两 大类。其一是系统正常 工作时的输入信号；其二是外加的测试信号，包括单位脉冲信号、 单位阶跃信号、单位斜坡信号、正弦信号和某些随机信号等。输 入信号的选择要综合考虑系统的工作条件和实验的目的。 3.3 一阶系统的时间响应 一、一阶系统 一阶系统传递函数的一般形式为 ( ) 1 ( ) ( ) + = = Ts K X s X s G s i o 式中， T 称为一阶系统的时间常数， K 称为一阶系统的增益。 二、一阶系统的单位脉冲响应w(t) ( ) [ ( )] 1 w t L X s o − = [ ( ) ( )] 1 L X s G s i = ⋅ − ] 1 [ 1 + = − Ts K L T t e T K − = ⋅ (t ≥ 0) w(t) 只有瞬态项，而其稳态项为零。即一阶系统的单位脉冲 响应函数是一个递减的指数函数。 对一阶系统而言，将其单位脉冲响应曲线衰减到初值的 之 前的过程定义为过渡过程，称此过程经历的时间为过渡过程时间 或调整时间，记为 。经过计算可得一阶系统的调整时间为 2% s t 4T 。 显然， 系统的时间常数 T 愈小， 其过渡过程的持续时间愈短， 亦 即系统的惯性愈小，系统对输入信号反应的快速性愈好

三、一阶系统的单位阶跃响应x() 20-.-G) =K0-e)u≥0) x)的瞬态项为-K片，其稳态项为K。即一阶系统的单位阶 跃响应函数是一个递增的指数函数。 对一阶系统而言，过渡过程还可定义为其阶跃响应增长到稳 态值的98%之前的过程，同样可算得相应的时间为4T。因此，时 间常数T确实反映了一阶系统的固有特性，其值愈小，系统的惯 性就愈小，系统的响应也就愈快。 四、线性系统输出与输入的关系 考察一阶系统的单位阶跃响应函数x()与单位脉冲响应函数 (),可知它们之间的关系为：元)=w),并且其输入的关系为： )=6)。事实上，对于任意线性系统而言，若一个输入A是另 一个输入B的导函数，则输入A所引起的输出就是输入B所引 起输出的导函数：同样地，若一个输入A是另一个输入B的积 分，则输入A所引起的输出就是输入B所引起输出的积分，但 是，如果积分是不定积分，则还需要确定积分常数。 3.4二阶系统的时间响应 一、二阶系统 二阶系统的传递函数有如下两种形式： 00克8+ (3.4.1)

三、一阶系统的单位阶跃响应 x (t) ou ( ) [ ( )] [ ( ) ( )] 1 1 x t L X s L G s X s ou o i = = ⋅ − − ] 1 1 [ 1 Ts s K L ⋅ + = − (1 ) T t K e − = − (t ≥ 0) x (t) ou 的瞬态项为 T t Ke − − ，其 稳态项为 K 。即一阶系统的单位阶 跃响应函数是一个递增的指数函数。 对一阶系统而言，过渡过程还可定义 为其阶跃响应增长到稳 态值的 98%之前的过程， 同样可算得相应的时间为 4T 。 因此， 时 间常数 T 确实反映了一阶系统的固有特性， 其值愈小， 系统的惯 性就愈小，系统的响应也就愈快。 四、线性系统输出与输入的关系 考察一阶系统的单位阶跃响应函数 与单位脉冲响应函数 ，可 知 它 们 之 间 的 关 系 为 ： x (t) ou w(t) x&ou (t) = w(t) ，并且其输入的关系为： u&(t) = δ (t) 。 事实上， 对于任意线性系统而言， 若一个输入 A 是 另 一个输入 B 的导函数，则输入 A 所引起的输出就是输入 B 所 引 起输出的导函数；同样地，若一个输入 A 是另一个输入 B 的 积 分，则输入 A 所引起的输出就是输入 B 所引起输出的积分，但 是，如果积分是不定积分，则还需要确定积分常数。 3.4 二阶系统的时间响应 一、二阶系统 二阶系统的传递函数有如下两种形式： 2 2 2 ( ) 2 ( ) ( ) n n n i o X s s s X s G s ξω ω ω + + = = （ 3.4.1）

或 G)=七国、 o2(s+四 (3.4.2) X,(s)）s2+250.5+m 其中，5是二阶系统的特征参数，它们表明二阶系统本身的与 外界无关的固有特性。一般将式(3.4.1)所示的系统称为无零点 的二阶系统或典型的二阶系统，而将式(3.4.2)所示的系统称为 有零点的二阶系统。在不特别声明的情况下，本章讨论的是典型 二阶系统的时间响应。 二阶系统的特征方程是 s2+250n3+o2=0, 此方程的两个特征根是 S2=-50n±onVE-l (3.4.3) 由式(3.4.3)可见，随着阻尼比取值的不同，二阶系统的特 征根分布不同，亦即二阶系统传递函数的极点分布不同，其分布 情况如图(3.4.1)所示。不同的极点分布情况，决定了二阶系统 在不同的阻尼情况下，其自由响应项不同。由图(3.4.1)可知， 当<0时，即二阶系统出现负阻尼时，其传递函数的两个极点分 布在[s]平面的右半平面内，系统不稳定。因此，这里只讨论≥0 时，二阶系统的响应情况。 [] 0<< =1 (6》 (c) 图(3.4.1)

或 2 2 2 2 ( ) ( ) ( ) ( ) n n n i o s s s X s X s G s ξω ω α α ω + + + = = （ 3.4.2） 其中， ω n ,ξ 是二阶系统的特征参数，它们表明二阶系统本身的与 外界无关的固有特性。一般将式（ 3.4.1）所示的系统称为无零点 的二阶系统或典型的二阶系统，而将式（ 3.4.2）所示的系统称为 有零点的二阶系统。在不特别声明的情况下，本章讨论的是典型 二阶系统的时间响应。 二阶系统的特征方程是 2 0, 2 2 s + ξω n s +ω n = 此方程的两个特征根是 1 2 s1,2 = −ξω n ±ω n ξ − （ 3.4.3） 由 式 （ 3.4.3） 可见， 随着阻尼比取值的不同， 二阶系统的特 征根分布不同，亦即二阶系统传递函数的极点分布不同，其分布 情况如图（ 3.4.1）所示。不同的极点分布情况，决定了二阶系统 在不同的阻尼情况下，其自由响应项不同。由图（ 3.4.1）可知， 当 ξ < 0 时 ，即二阶系统出现负阻尼时，其传递函数的两个极点分 布 在 [s]平面的右半平面内，系统不稳定。因此，这里只讨论 ξ ≥ 0 时，二阶系统的响应情况。 图 （ 3.4.1）

二、二阶系统的单位脉冲响应)和单位阶跃响应 在不同阻尼系数下，二阶系统的单位脉冲响应和单位阶 跃响应如表3.4.1所示。 表3.4.1二阶系统的单位脉冲响应w)和单位阶跃响应 阻尼系数 单位脉冲响应() 单位阶跃响应 5=0 x()=1-cos0,1 无阻尼 w(t)=@,sin@t 01 x0= x(0=1 o。ee 过阻尼 2g9- 其中，o4=0nV-2，称o。为二阶系统的有阻尼固有频率： 5=-(5+V2-1)m:52=-(5-V2-1)m。 当取值不同时，二阶欠阻尼系统的单位脉冲响应曲线如图 3.42所示。由图可知，欠阻尼系统的单位脉冲响应曲线是减幅 的正弦振荡曲线，且5愈小，衰减愈慢，振荡频率四愈大。故欠 阻尼系统又称为二阶振荡系统，其幅值衰诚的快慢取决于和。 （光称为时间衰减常数，记为。)：

二、二阶系统的单位脉冲响应w(t)和单位阶跃响应 在不同阻尼系数下，二阶系统的单位脉冲响应 和单位阶 跃响应如表 3.4.1 所示。 w(t) 表 3.4.1 二阶系统的单位脉冲响应 w(t) 和单位阶跃响应 阻尼系数 单位脉冲响应w(t) 单位阶跃响应 ξ = 0 无阻尼 w t t ω n ω n ( ) = sin x t t o ω n ( ) = 1− cos 0 1 过阻尼 ( ) 2 1 ( ) 2 1 2 n s t s t o x t e − e − = ξ ω ( ) 2 1 ( ) 1 1 2 2 1 2 s e s e x t s t s t n o − − − − = + ξ ω 其中， 2 ω d = ω n 1−ξ ， 称 ω d 为二阶系统的有阻尼固有频率； n s (ξ ξ 1)ω 2 1 = − + − ； n s (ξ ξ 1)ω 2 2 = − − − 。 当 ξ 取值不同时，二阶欠阻尼系统的单 位脉冲响应曲线如图 3.4.2 所示。由图可知，欠阻尼系统的单位脉 冲响应曲线是减幅 的正弦振荡曲线， 且 ξ 愈小， 衰减愈慢， 振荡频率 ω d 愈大。 故 欠 阻尼系统又称为二阶振荡系统，其 幅值衰减的快慢取决于 ξω n （ ξω n 1 称为时间衰减常数，记为 σ ）

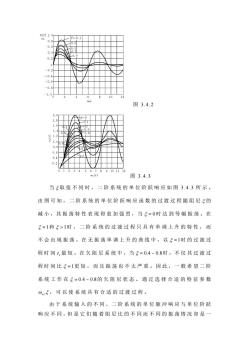
图3.4.2 912345 89101112 图3.4.3 当5取值不同时，二阶系统的单位阶跃响应如图3.4.3所示。 由图可知，二阶系统的单位阶跃响应函数的过渡过程随阻尼的 减小，其振荡特性表现得愈加强烈，当5-0时达到等幅振荡。在 5=1和>1时，二阶系统的过渡过程只具有单调上升的特性，而 不会出现振荡。在无振荡单调上升的曲线中，以5=1时的过渡过 程时间1，最短。在欠阻尼系统中，当5=0.4~0.8时，不仅其过渡过 程时间比=1更短，而且振荡也不太严重。因此，一般希望二阶 系统工作在ξ=0.4~0.8的欠阻尼状态。通过选择合适的特征参数 ⊙，5，可以使系统具有合适的过渡过程。 由于系统输入的不同，二阶系统的单位脉冲响应与单位阶跃 响应不同，但是它们随着阻尼比的不同而不同的振荡情况却是

图 3.4.2 图 3.4.3 当 ξ 取值不同时，二阶系统的单位阶跃响应如图 3.4.3 所示。 由图可知，二阶系统的单位阶跃响应 函数的过渡过程随阻尼 ξ 的 减小，其振荡特性表现得愈加强烈，当 ξ = 0 时达到等幅振荡。在 ξ = 1和 ξ > 1时，二阶系统的过渡过程只具有单 调上升的特性，而 不会出现振荡。 在无振荡单调上升的曲线中， 以 ξ = 1时的过渡过 程时间 ts 最短。在欠阻尼系统中，当 ξ = 0.4 ~ 0.8时 ，不仅其过渡过 程时间比 ξ = 1更短， 而且振荡也不太严重。 因此， 一般希望二阶 系统工作在 ξ = 0.4 ~ 0.8的欠阻尼状态。通过选择合适的特征参数 ω n ,ξ ，可以使系统具有合适的过渡过程。 由于系统输入的不同，二阶系统的单位脉冲响应与单位阶跃 响应不同，但是它们随着阻尼比的不同而不同的振荡情况却是一

致的。当系统为无阻尼系统时，均为等幅振荡；当系统为欠阻尼 系统时，均为减幅振荡：而当系统为临界阻尼或过阻尼系统时， 均不会出现振荡。 三、二阶欠阻尼系统响应的性能指标 二阶欠阻尼系统的单位阶跃响应曲线如图3.4.4所示，其瞬 态性能指标包括上升时间，、峰值时间。、最大超调量M。、调整 时间1，、振荡次数N等。 1,上升时间(，：响应曲线从原工作状态出发，第一次达到输出 稳态值所需的时间定义为上升时间。 -arctan 1,= 当5一定时，0n增大，1，就减小；当o。一定时，5增大，1，就 增大。 r.( M/不 允许误差 0.05成002 图3.4.4 2,峰值时间t。：响应曲线达到第一个峰值所需的时间定义为峰 值时间。 6品 当5一定时，on增大，1，就减小；当0，一定时，增大，1n就 增大

致的。当系统为无阻尼系统时，均为等幅振荡；当系统为欠阻尼 系统时，均为减幅振荡；而当系统为临界阻尼或过阻尼系统时， 均不会出现振荡。 三、二阶欠阻尼系统响应的性能指标 二阶欠阻尼系统的单位阶跃响应曲线如图 3.4.4 所示，其瞬 态性能指标包括上升时间 、峰值时间 、最大超调量 、调 整 时 间 、振荡次数 等 。 r t p t M p s t N 1．上升时间 ：响应曲线从原工作状态出发，第一次达到输出 稳态值所需的时间定义为上升时间。 r t d r t ω ξ ξ π 2 1 arctan − − = 当 ξ 一定时， ω n 增大， tr 就减小；当 ω n 一定时， ξ 增大， 就 增大。 r t 图 3.4.4 2．峰值时间 ：响应曲线达到第一个峰值所需的时间定义为峰 值时间。 p t d p t ω π = 当 ξ 一定时， ω n 增大， t p 就减小；当 ω n 一定时， ξ 增大， 就 增大。 p t

3,最大超调量M。：一般用下式定义系统的最大超调量，即 M,=,)-四x10% x(co) 亦即 Mp=exp(-5r/V1-52)x100%. 因此，M,与0.无关，而只与5有关。增大，M,就减小；反 之亦然。 4.调整时间1，：在过渡过程中，x()取的值满足下面不等式时所 需要的时间，定义为调整时间。不等式为 x()-x(o≤△·x(o) (121,) 4+ln- 1 5+ln- 当A=2%时，4,260。 V1-5.当△=5%时，1,2之 若0<501，上述关系变成*和*品 3 当一定时，0增大，1，就减小；当0。一定时，增大，1，也 减小。 5.振荡次数N:在过渡过程时间内，x)穿越其稳态值x(o)的 次数的一半定义为振荡次数。即 N-210 当0<5<07,4=2%时，N=21-F π5 当0<5<07,4=5%时，N.15-型 振荡次数N随着的增大而减小，它的大小直接反映了系统 的阻尼特性。 从二阶系统的瞬态性能指标与其特征参数之间的关系中可

3．最大超调量 M p ：一般用下式定义系统的最大超调量，即 100%. ( ) ( ) ( ) × ∞ − ∞ = o o p o p x x t x M 亦 即 exp( / 1 ) 100%. 2 M p = −ξπ −ξ × 因此， M p 与 ω n 无关， 而只与 ξ 有关。 ξ 增大， 就减小； 反 之亦然。 M p 4．调整时间 ：在过渡过程中， 取的值满足下面不等式时所 需要的时间，定义为调整时间。不等式为 s t x (t) o ( ) − (∞) ≤ ∆ ⋅ (∞) o o o x t x x （ t ≥ ts ） 当 ∆ = 2%时 ， n s t ξω ξ2 1 1 4 ln − + ≥ ； 当 ∆ = 5% 时 ， n s t ξω ξ2 1 1 5 ln − + ≥ 若 0 < ξ < 0.7，上述关系变成 n s t ξω 4 ≈ 和 n s t ξω 3 ≈ 当 ξ 一定时， ω n 增大， ts 就减小；当 ω n 一定时， ξ 增大， 也 减小。 s t 5．振荡次数 ：在过渡过程时间内， 穿越其稳态值 的 次数的一半定义为振荡次数。即 N x (t) o (∞) o x d s t N 2π /ω = 当 0 < ξ < 0.7， ∆ = 2%时 ， πξ ξ2 2 1− N = ； 当 0 < ξ < 0.7， ∆ = 5% 时 ， πξ ξ2 1.5 1− N = 。 振荡次数 N 随 着 ξ 的增大而减小，它的大小直接反映了系统 的阻尼特性。 从二阶系统的瞬态性能指标 与其特征参数之间的关系中可

以看出： ()系统性能指标的矛盾性。一般说来，系统的上升时间1，、 峰值时间‘。等反映系统响应快速性的性能指标与最大超调量 M。、振荡次数N等指标是相互矛盾的。 (2)为了使二阶系统具有满意的动态特性，必须合理选择系 统的阻尼比5和无阻尼固有频率。一般的做法是先根据最大超 调量M。、振荡次数N等要求选择系统的阻尼比：，然后再根据上 升时间4、峰值时间。、调整时间1，等要求，确定系统无阻尼固 有频率D。 需要说明的是，以上各个性能指标的公式是从典型二阶欠系 统的阶跃响应中推导出米的。如果系统是具有零点的二阶系统， 这些公式是不能直接应用的。但是，其性能指标同二阶系统特征 参数之间的变化趋势却保持不变。 3.5高阶系统的响应分析 一个高阶系统的时间响应可以由若干个一阶系统和二阶系 统的时间响应叠加而成。结合本章第一节的结论，还可以得到主 导极点的概念。 若在系统传递函数的极点分布中，其中一对共轭极点离虚轴 的距离较近，而其它所有极点离虚轴距离是该对共轭极点离虚轴 距离的5倍以上，且这对极点附近没有零点，则称此对极点为系 统的主导极点。在研究高阶系统的过渡过程时可以将系统的过渡 过程近似地由主导极点所决定的二阶振荡系统的过渡过程代替

以看出： (1)系统性能指标的矛盾性。一般说来，系统的上升时间 、 峰值时间 等反映系统响应快速性的性能指标与最大超调量 、振荡次数 等指标是相互矛盾的。 r t p t M p N (2)为了使二阶系统具有满意的动态 特性，必须合理选择系 统的阻尼比 ξ 和无阻尼固有频率 ω n 。 一般的做法是先根据最大超 调 量 M p 、振荡次数 N 等要求选择系统的阻尼比 ξ ，然后再根据上 升时间 、峰值时间 、调整时间 等要求，确定系统无阻尼固 有频率 r t p t s t ω n 。 需要说明的是，以上各个性能指标的公式是从典型二阶欠系 统的阶跃响应中推导出来的。如果系统是具有零点的二阶系统， 这些公式是不能直接应用的。但是，其性能指标同二阶系统特征 参数之间的变化趋势却保持不变。 3.5 高阶系统的响应分析 一个高阶系统的时间响应可 以由若干个一阶系统和二阶系 统的时间响应叠加而成。结合本章第一节的结论，还可以得到主 导极点的概念。 若在系统传递函数的极点分布中，其中一对共轭极点离虚轴 的距离较近，而其它所有极点离虚轴距离是该对共轭极点离虚轴 距离的 5 倍以上，且这对极点附近没有零点，则称此对极点为系 统的主导极点。在研究高阶系统的过渡过程时可以将系统的过渡 过程近似地由主导极点所决定的二阶振荡系统的过渡过程代替