《机械控制工程基础》课程教学资源（PPT课件）第四章 频率特性分析

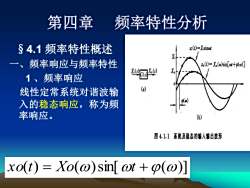
第四章 频率特性分析 §4.1频率特性概述 (t)=Xisinat 一、 频率响应与频率特性 0)=X(sin[t+)] 1、频率响应 酒型 线性定常系统对谐波输 (a 入的稳态响应，称为频 率响应。 (b 图4.1.1系统及稳态的输人输出被形 xo(t)=Xo(o)sin[ot+o(@)]

第四章 频率特性分析 §4.1 频率特性概述 一、频率响应与频率特性 1 、频率响应 线性定常系统对谐波输 入的稳态响应，称为频 率响应。 x o(t) = Xo()sin[t +()]

K 例1设传递函数为 G(S)= Ts+1 x;(t)=X;si ot 设输入信号为 X,(S)= X,0 s2+0 2 则输出为 K X,0 X(s)=G(s)X,(S)= Ts+1 s2+@2 X,KT@ X K x,(t)= ●e-tlT sin(ot -arctan To) 1+T2o2 V1+T2@2 系统的稳态响应 X K x,(t)= sin(ot-arctan To) v+T@2

例1 设传递函数为 1 ( ) + = Ts K G s 设输入信号为 2 2 ( ) ( ) sin    + = = s X X s x t X t i i i i 则输出为 2 2 1 ( ) ( ) ( )   + • + = = s X Ts K X s G s X s i o i sin( arctan ) 1 1 ( ) 2 2 / 2 2      t T T X K e T X KT x t i t T i o − + • + + = − 系统的稳态响应 sin( arctan ) 1 ( ) 2 2    t T T X K x t i o − + =

系统输出的幅值 XK X(o)三 V1+T202 系统输出的相位 p(o) =-arctan To 频率响应只是时间响应的一个特例。当谐波 频率不同时，其输出的幅值与相位也不同

系统输出的幅值 2 2 1 ( )   T X K X i o + = 系统输出的相位 () = −arctan T 频率响应只是时间响应的一个特例。当谐波 频率不同时，其输出的幅值与相位也不同

2频率特性 幅频特性：线性系统在谐波输入作用下，其稳定输出与输 入的幅值比，即 Xo(@) A(⊙)= X 相频特性：稳态输出信号与输入信号的相位差。 相位逆时针为正，顺时针为负。 相位超前为正，相位滞后为负。 A(o)·∠p(o) 对物理系统相位一般都是滞后的。 幅频特性和相频特性总称为频率特性。 A(o)e()

2 频率特性 幅频特性：线性系统在谐波输入作用下，其稳定输出与输 入的幅值比，即 相频特性：稳态输出信号与输入信号的相位差。 相位逆时针为正，顺时针为负。 相位超前为正，相位滞后为负。 对物理系统相位一般都是滞后的。 幅频特性和相频特性总称为频率特性。 Xi Xo A ( ) ( )   = 记作 A() • () 或 ( ) ( )    j A e

二频率特性与传递函数的关系 设系统的微分方程为： a,x(t)+axmD(t)+.+a&(t)+aoxo(t) =bmxm)(t)+bm1xm-少()）+.+b,()+box,() 系统传递函数为 G(S)= Y(s)_bns"+bm-1sm1+.+b3+b。 X,(s) anS”+an-1s++a1S+a。 当输入信号为 x;(t)=X,si ot 即 Xω X,(S)= s2+2

二 频率特性与传递函数的关系 设系统的微分方程为： ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 0 ( 1) 1 ( ) 1 0 ( 1) 1 ( ) b x t b x t b x t b x t a x t a x t a x t a x t i i m m i m m i o o n n o n n o = + + + + + + + + − − − −     系统传递函数为 o n n n n o m m m m i o a s a s a s a b s b s b s b X s X s G s + + + + + + + + = = − − − − 1 1 1 1 1 1 ( ) ( ) ( )   当输入信号为 x t X t i ( ) = i sin  即 2 2 ( )   + = s X X s i i

系统的输出 X。(s)=G(s)X,(s)= bns+bm-s-1++bs+b2。X,0 ans”+an-s-+.+a4+a。s2+ 2 若系统无重极点 X)=2 B ,B s-S s-jo s+ja x(1)=>A,e+(Belo+B*e-jo) i=1 稳态响应为 x(t)=Bejo+B*e-jor

系统的输出 2 2 1 1 1 1 1 1 ( ) ( ) ( )   + • + + + + + + + + = = − − − − s X a s a s a s a b s b s b s b X s G s X s i o n n n n o m m m m o i   若系统无重极点 ( ) ( ) * 1  s j B s j B s s A X s n i i i o + + − + − = = ( ) ( * ) 1 j t j t n i s t o i x t A e Be B e i  −  = =  + + 稳态响应为 j t j t o x t Be B e  −  ( ) = + *

若系统含有k重极点，则输出含 te(U=1,2,.k-1) 对于稳定系统，由于s的实部为负， 的增长没有 e 的衰减快。所以te 随着t→o0 也趋于零。 X,⊙ B-G(5)(s-joXs+j0) s-j0) =G(S) X,0 s=jo (s+j0)s=j0 Go.-G(jpm. 2j X -2j ,()=G(jo)X elo+GUo-eo+ZG(jo) 则稳态响应为 2j =G(j@)X;sin[@t+ZG(j@)]

若系统含有k重极点，则输出含 t e ( j = 1,2, k −1) k s t j  对于稳定系统，由于sj的实部为负， k t 的增长没有 s t j e 的衰减快。所以 k s t j t e 随着 t →  也趋于零。 j X G j e j X G j s j X s j G s s j s j X B G s i j G j i s j i s j i 2 ( ) 2 ( ) ( ) ( ) ( ) ( )( ) ( ) ( ) = • = • + − = − + =  = =            j X G j e j X B G j i j G j i 2 ( ) 2 * ( ) ( ) − = • − = − • −     则稳态响应为 ( ) sin[ ( )] 2 ( ) ( ) [ ( )] [ ( )]         G j X t G j j e e x t G j X i j t G j j t G j o i = +  − = + − +

系统的幅频和相频特性分别为 A(0)= Xo(0) =G(jo川 Xi p(o)=∠G(jo) 故 G(jo)G(Ujo)川eGUo) 就是系统的频率特性。量纲同传递函数。 由于Gω)是一个复变函数，可以写成实部和虚部之和， 即 G(j@)=Re[G(j@)]+Im[G(j@)]=u(@)+jv@) 实频特性 v(@) 虚频特性

系统的幅频和相频特性分别为      =  = = ( ) ( ) | ( ) | ( ) ( )       G j G j Xi Xo A 故 ( ) ( ) | ( ) |    j G j G j G j e  = 就是系统的频率特性。量纲同传递函数。 由于G(jω)是一个复变函数，可以写成实部和虚部之和， 即 G(j) = Re[G(j)]+ Im[G(j)] = u() + jv() u() 实频特性 v() 虚频特性

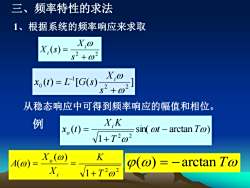
三、频率特性的求法 1、根据系统的频率响应来求取 X,0 X,(s)= s2+02 xo(t)=L[G(s) X,0 从稳态响应中可得到频率响应的幅值和相位。 例 x(t)= XK sin(ot -arctan To) V1+T2o K A(0)= X.(@) (@)=-arctan To X V1+T2@

三、频率特性的求法 1、根据系统的频率响应来求取 2 2 ( )   + = s X X s i i ( ) [ ( ) ] 2 2 1 0   + = − s X x t L G s i 从稳态响应中可得到频率响应的幅值和相位。 sin( arctan ) 1 ( ) 2 2    t T T X K x t i o − + 例 = 2 2 1 ( ) ( )    T K X X A i o + = = () = −arctan T

2、将传递函数中的s换为jω(sj)来求取 将系统的传递函数G(s)中的s换为j四， 即为系统的频率特性。 G(j@)=G(s)s-J0 K K ejarctanTo 1+iTo v1+T2@2 K A()= X.(@) p(⊙) =-arctan To X V1+T202 x (t)=X G(s)sin[@t+G(s)] X,K sin(ot-arctan To) v1+T2@

2、 将传递函数中的s 换为jω（s=jω）来求取 将系统的传递函数G(s)中的s换为jω， 即为系统的频率特性。      j T s j e T K j T K G j G s arctan 2 2 1 1 ( ) ( ) − = + = + = = 2 2 1 ( ) ( )    T K X X A i o + = = () = −arctan T sin( arctan ) 1 ( ) ( ) sin[ ( )] 2 2     t T T X K x t X G s t G s i o i − + = = + 