《机械控制工程基础》课程教学资源（PPT课件）第五章 系统的稳定性

第五章 系统的稳定性 5.1系统稳定性的初 步概念 一、系统不稳定现象 的发生 y(r) B 负载 活塞

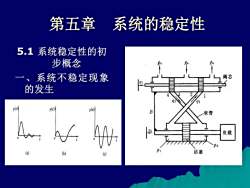
第五章 系统的稳定性 5.1 系统稳定性的初 步概念 一、系统不稳定现象 的发生

◆首先，线性系统不稳定现象发生与否，取 决于系统内部条件，而与输入无关。 ◆其次，系统发生不稳定现象必有适当的反 馈作用。 ◆第三，控制理论所讨论的稳定性其实都是 指自由振荡下的稳定性

◆首先，线性系统不稳定现象发生与否，取 决于系统内部条件，而与输入无关。 ◆其次，系统发生不稳定现象必有适当的反 馈作用。 ◆第三，控制理论所讨论的稳定性其实都是 指自由振荡下的稳定性

二、稳定的定义和条件 若系统在初始状态（不论是无输入时的初态，还是输 入引起的初态)的影响下，由它所引起的系统的时间 响应随着时间的推移，逐渐衰减并趋向于零，则该系 统为稳定的。 方法(1) 对于阶定常线性系统微分方程，拉氏变换后得到 X(s)= M X,(s)+ N(s) M(s) D(s) =G(s)为系统的传递函数 D(s) D(s) N(s)是与初始条件x(0)有关的s多项式，而x(0) 是输出x,(t)及其各阶导数x,)(t)在输入作用前t=0时刻 的值，即系统在输入前的初始状态

二、稳定的定义和条件 若系统在初始状态（不论是无输入时的初态，还是输 入引起的初态）的影响下，由它所引起的系统的时间 响应随着时间的推移，逐渐衰减并趋向于零，则该系 统为稳定的。 方法（1） 对于n阶定常线性系统微分方程，拉氏变换后得到 ( ) ( ) ( ) ( ) ( ) ( ) D s N s X s D s M s X s o = i + ( )为系统的传递函数 ( ) ( ) G s D s M s = 的值，即系统在输入前的初始状态。 是输出 及其各阶导数 在输入作用前 时刻 是与初始条件 有关的 多项式，而 ( ) ( ) 0 ( ) (0 ) s (0 ) ( ) ( ) ( ) = − − x t x t t N s x x k o o k o k o

稳定性就是研究初始状态下的输出情况。系统在初始 状态下的输出为 N(s) X(s)= D(s) 当特征方程的根各不相同时，系统的输出为 0=L'x,（s=t ]=∑Ae4 若系统的特征方程的根实部均为负值，即Re[si]<0, 则零输入响应最终将衰减为零。这样系统就是稳定的。 系统的输入项参数对系统稳定性没有影响，即传递函数 的零点对系统的稳定性无影响

稳定性就是研究初始状态下的输出情况。系统在初始 状态下的输出为 ( ) ( ) ( ) D s N s X s o = 当特征方程的根各不相同时，系统的输出为 s t n i o o i i A e D s N s x t L X s L = − − = = = 1 1 1 ] ( ) ( ) ( ) [ ( )] [ 若系统的特征方程的根实部均为负值，即Re[si]<0， 则零输入响应最终将衰减为零。这样系统就是稳定的。 系统的输入项参数对系统稳定性没有影响，即传递函数 的零点对系统的稳定性无影响

方法(2) 若对线性系统在初始状态为零时输入单位脉冲函数，单 位脉冲响应的形式于零输入响应形式相同。所以当单位 脉冲响应趋于零时，系统则稳定。 综上所述，系统稳定的充要条件：系统的全部特征跟 都具有负实部。即系统传递函数的全部极点均位于[s] 平面的左半平面，系统则稳定

方法（2） 若对线性系统在初始状态为零时输入单位脉冲函数，单 位脉冲响应的形式于零输入响应形式相同。所以当单位 脉冲响应趋于零时，系统则稳定。 s t n i i i A e D s M s w t L G s L = − − = = = 1 1 1 ] ( ) ( ) ( ) [ ( )] [ 综上所述，系统稳定的充要条件：系统的全部特征跟 都具有负实部。即系统传递函数的全部极点均位于[s] 平面的左半平面，系统则稳定

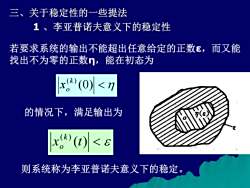
三、关于稳定性的一些提法 1、李亚普诺夫意义下的稳定性 若要求系统的输出不能超出任意给定的正数E,而又能 找出不为零的正数n,能在初态为 x(0)<7 的情况下，满足输出为 x(t)<a 则系统称为李亚普诺夫意义下的稳定

三、关于稳定性的一些提法 1 、李亚普诺夫意义下的稳定性 若要求系统的输出不能超出任意给定的正数ε，而又能 找出不为零的正数η，能在初态为 (0)  (k ) o x 的情况下，满足输出为 ( )   ( ) x t k o 则系统称为李亚普诺夫意义下的稳定

2、渐近稳定性 渐近稳定就是线性系统稳定性的定义。系统若是渐近 稳定，就一定是李亚普诺夫意义下的稳定，反之不然。 3、“小偏差”稳定性 “小偏差”稳定性又称“局部稳定性”。系统一般都 具有非线性，在小范围内系统是稳定的，在大范围 内系统就不一定稳定

2 、渐近稳定性 3、 “小偏差”稳定性 渐近稳定就是线性系统稳定性的定义。系统若是渐近 稳定，就一定是李亚普诺夫意义下的稳定，反之不然。 “小偏差”稳定性又称“局部稳定性”。系统一般都 具有非线性，在小范围内系统是稳定的，在大范围 内系统就不一定稳定

§5.2 Routh(劳斯)稳定判据 一、系统稳定的必要条件 D(s)=ans”+an-1s"+.+a,s+a,=0 +an-ls+.+ s”+ a5+0=(s-5s-52)s-3) a an an -0-6-)=r-位r1+(2s,+-8 0 an-2 an i=1,j=2 i<i

§5.2 Routh（劳斯）稳定判据 一、 系统稳定的必要条件 i n i n n n i j i j i j n n n i i n n i n i n n n i j i j i j n n i i n n n n n n n n n n n n n s a a s s a a s a a s s s s s s s s s s s s s s s s s s s a a s a a s a a s D s a s a s a s a 1 0 1, 2 2 1 1 1 2 1, 2 1 1 1 2 1 2 1 1 1 0 1 0 1 1 ( 1) ( ) ( ) ( )( ) ( ) ( ) ( ) ( 1) ( )( ) ( ) ( ) 0 =  = = − = − = −  = = − = − − − − = −  = = − − − − = − + − + −  + + + + = − − − = + + + + =          

要使全部特征根均具有负实部，必须满足两 个条件，即必要条件： 1)特征方程的各项系数ai都不为零。因为 若有一系数为零，则必出现实部为零的特 征根或实部有正有负的特征根，此时系统 为临界稳定或不稳定。 2)特征方程的各项系数ai的符号都相同

要使全部特征根均具有负实部，必须满足两 个条件，即必要条件： 1）特征方程的各项系数ai都不为零。因为 若有一系数为零，则必出现实部为零的特 征根或实部有正有负的特征根，此时系统 为临界稳定或不稳定。 2）特征方程的各项系数ai的符号都相同