《经济数学基础》课程PPT教学课件（线性代数）第一章 行列式（2/2）

五.行列式按行（列）展开 对于三阶行列式，容易验证： 01112 13 22 L23 21 21 23 L21 L22 L23 二32 2 33 31 33 33 L31 L32 L33 可见一个三阶行列式可以转化成三个二阶行列式的计算。 问题：一个n阶行列式是否可以转化为若干个n一1阶行列式 来计算？

1 五. 行列式按行（列）展开 对于三阶行列式，容易验证： 31 32 33 21 22 23 11 12 13 a a a a a a a a a 3 1 3 3 2 1 2 3 1 3 3 1 3 3 2 1 2 3 1 2 3 2 3 3 2 2 2 3 1 1 a a a a a a a a a a a a a a = a − + 可见一个三阶行列式可以转化成三个二阶行列式的计算。 问题：一个n 阶行列式是否可以转化为若干个n－1 阶行列式 来计算？

定义1：在n阶行列式中，把元素4， 所在的第i行和 第j列划去后，余下的n一1阶行列式叫做元素 a的余子式。记为M 称A=（-1)M 为元素，的代数余子式。 12 3 14 L11 L12 014 例如：D= 21.2223.24 M23= 31 L32 L34 31 32 33 L34 an L42 L44 041 42 d43 L44 A23=(-1)2*3M23=-M23· 2

2 定义1： 在 n 阶行列式中，把元素 ij a 所在的第 i 行和 第 j 列划去后，余下的n－1 阶行列式叫做元素 ij a 的 余子式。记为 Mij 称 ( ) ij i j Aij M + = − 1 为元素 ij a 的代数余子式。 例如： 41 42 43 44 31 32 33 34 21 22 23 24 11 12 13 14 a a a a a a a a a a a a a a a a D = 41 42 44 31 32 34 11 12 14 23 a a a a a a a a a M = ( ) 23 2 3 A23 1 M + = − . = −M23

L21 L23 L24 D M2= 31 L33 L34 as L43 L44 A2=(-1)2M1F-M2 L12 13 M44= L21 L22 023 L31 L32 L33 A4=（-1)4M4=M4 注：行列式的每个元素都分别对应着一个余子式和一个 代数余子式。 3

3 41 42 43 44 31 32 33 34 21 22 23 24 11 12 13 14 a a a a a a a a a a a a a a a a D = 41 43 44 31 33 34 21 23 24 12 a a a a a a a a a M = ( ) 12 1 2 A12 1 M + = − = −M12 31 32 33 21 22 23 11 12 13 44 a a a a a a a a a M = ( ) 44 44 4 4 A44 = − 1 M = M + 注：行列式的每个元素都分别对应着一个余子式和一个 代数余子式

定理1： 行列式等于它的任一行（列）的各元素与其对应 的代数余子式乘积之和，即 D=a1A1+2A2+.+anAm（i=1,2,n) 证明： (先特殊，再一般) 分三种情况讨论，我们只对行来证明此定理。 (I) 假定行列式D的第一行除41外都是0。 0 0 D L21 2 @2n Am An2 (rn 4

4 行列式等于它的任一行（列）的各元素与其对应 的代数余子式乘积之和，即 D = ai1Ai1 + ai 2Ai 2 ++ ainAin (i = 1,2,  ,n) 定理1： 证明： （先特殊，再一般） 分三种情况讨论，我们只对行来证明此定理。 (1) 假定行列式D的第一行除 11 a 外都是 0 。 n n nn n a a a a a a a D       1 2 21 22 2 11 0 0 =

由行列式定义，D中仅含下面形式的项 (-1)）r.a142,43y.0. =a1(-l)）raha>a2aa3h.0 其中（-1)6'a方.0.恰是M1的一般项。 所以，D=M1 =4(-1)+1M =41A1

5 由行列式定义，D 中仅含下面形式的项 n n j j nj j j j a a a a  2 3 2 3 11 2 3 (1, , , , ) ( 1)  − n n j j nj j j j a a a a  2 3 2 3 2 3 (1, , , , ) 11 ( 1)  = − 其中 n n j j nj j j j a a a  2 3 2 3 2 3 (1, , , , ) ( 1)  − 恰是 M11 的一般项。 所以， D = a11M11 11 1 1 11 a ( 1) M + = − = a11A11

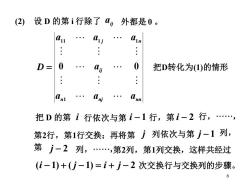
(2) 设D的第i行除了外都是0。 j : D= 0 0 把D转化为(1)的情形 : 。 把D的第i行依次与第i-1行，第i-2行，.， 第2行，第1行交换；再将第j列依次与第j-1列， 第j-2列，.，第2列，第1列交换，这样共经过 (i-1)+(j-1)=i+j-2次交换行与交换列的步骤。 6

6 (2) 设 D 的第 i 行除了 ij a 外都是 0 。 n nj nn ij j n a a a a a a a D             1 11 1 1 = 0 0 把D转化为(1)的情形 把 D 的第 i 行依次与第 i − 1 行，第 i − 2 行，······， 第2行，第1行交换；再将第 j 列依次与第 j − 1 列， 第 j − 2 列，······，第2列，第1列交换，这样共经过 (i − 1) + ( j − 1) = i + j − 2 次交换行与交换列的步骤

由性质2，行列式互换两行（列）行列式变号， 得， 0 0 : D=(-1)+i- Ai-1,j li-1, .: : 心d 0n,j-1 nn =(-1)+aM,=(-1)+A

7 由性质2，行列式互换两行（列）行列式变号， 得， nj n j nn i j i j i n i j i j a a a a a a a D             , 1 1, 1, 1 1, 2 0 0 ( 1) − − − − − + − = − ij i j ij ij i j a M A + + = (−1) = (−1)

(3) 一般情形 12 n .: D= n n m . Am Am2 11 2 =41+0+.+00+42+.+0 0+.+0+4m : 2 n 8

8 (3) 一般情形 n n nn i i in n a a a a a a a a a D            1 2 1 2 11 12 1 = n n nn i i i n n a a a a a a a a a               1 2 1 2 11 12 1 = + 0 + + 0 0 + + + 0 0 + + 0 +

2 . n 2 : : : .: ·: 0 0 0 Ap 0 +.十 0 0 Ain : : . 4n2 =a1A1+a2A2+.+0nAm (i=1,2,.,n) 证毕。 -3-53 例如，行列式D= 0-1 0 按第一行展开，得 72 -10 722 0 D=-3 +5

9 n n nn i n a a a a a a a            1 2 1 11 12 1 = 0 0 n n nn i n a a a a a a a            1 2 2 11 12 1 + 0 0 n n nn in n a a a a a a a             1 2 11 12 1 + + 0 0 = ai1Ai1 + ai 2Ai 2 ++ ainAin (i = 1,2,  ,n) 例如，行列式 7 7 2 0 1 0 3 5 3 − − − D = 7 2 1 0 3 − D = − 按第一行展开，得 7 2 0 0 + 5 7 7 0 1 3 − + 证毕

定理2： 行列式任一行（列)的元素与另一行（列）的对应 元素的代数余子式乘积之和等于零，即 k1A1+0k2A2+.+0An=0,k≠i. 证明： 由定理1，行列式等于某一行的元素分别与它们 代数余子式的乘积之和。 12 da (l2 Ain 在D= 中，如果令第i行的元素等于 Qki Ak2 kn 另外一行，譬如第k行的元素 0m2 Cnn 10

10 行列式任一行（列）的元素与另一行（列）的对应 元素的代数余子式乘积之和等于零，即 0, . 1 1 2 2 a A a A a A k i k i + k i ++ kn i n =  定理2： 证明： 由定理1，行列式等于某一行的元素分别与它们 代数余子式的乘积之和。 在 n n nn k k kn i i in n a a a a a a a a a a a a D                 1 2 1 2 1 2 11 12 1 = 中，如果令第i 行的元素等于 另外一行，譬如第k 行的元素