《经济数学基础》课程PPT教学课件（微积分）第6章 定积分的应用

第6章定积分的应用 6.1定积分的几何应用 6.2定积分在经济问题中的应用 结束

6.1 定积分的几何应用 6.2 定积分在经济问题中的应用 第6章 定积分的应用 结束

6.1定积分的几何应用 6.1.1微元法： 以曲边梯形面积为例如图曲边梯形 1.选取一个变量为积分变量，并确定其变化区间4，b], 在区间上任取一小区间并记为[x,x+dx] 2.以点x处的函数值为高，以[x,x+dx]为底的矩形面 积做为△A的近似值△4≈f由x)dx称为面积微 元，记为 dA=f(x)压是面积为 A=JdA=∫fw)dx ax x+dx b 此方法称为微元法或积分元素法， 前页后页结束

前页 后页 结束 2.以点x处的函数值为高,以[x,x+dx]为底的矩形面 积做为△A的近似值 ,其中f(x)dx 称为面积微 元,记为 , 于是面积为 1.选取一个变量为积分变量，并确定其变化区间[a,b], 在区间上任取一小区间并记为 . 此方法称为微元法或积分元素法. [ d ] x, x + x 6.1.1 微元法:   A f x x ( )d d ( )d A f x x = d ( )d b b a a A A f x x = =   a x x x + d b A 6.1 定积分的几何应用 以曲边梯形面积为例,如图曲边梯形

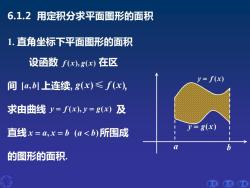
6.1.2用定积分求平面图形的面积 1.直角坐标下平面图形的面积 设函数f(x),g(x)在区 y=f(x) 间【a,b]上连续，g(x)≤f(x), 求由曲线y=f(x),y=g(x)及 直线x=a,x=b(a<b)所围成 y=8(x) 的图形的面积. 前页后页结束

前页 后页 结束 设函数 在区 间 上连续, , 求由曲线 及 直线 所围成 的图形的面积. 1. 直角坐标下平面图形的面积 6.1.2 用定积分求平面图形的面积 f x g x ( ), ( ) [ , ] a b g x f x ( ) ( ) ≤ y f x y g x = = ( ), ( ) x a x b a b = =  , ( ) y f x = ( ) y g x = ( ) a b

分)在区间 旺取小区间 ,设此☒间上的面 积为，它近似于高为 ,底为 的短形面积从雨得 面积微元为 dA=[f(x)-g(x)ldx. (2)以【f(x)-g为罅积表达式，在区间 作定积分 就是所座形的面恐)dx 在这个公式中，无论曲线 y=f(x) 在x轴的上方或下方都成立，只 要y=g(x)在曲线y=f(x)的下方 即可。 =8(x) a xx+dx b 前页后页结求

前页 后页 结束 (2) 以 为被积表达式,在区间 作定积分 就是所求图形的面积. (1) 在区间 上任取小区间 ,设此小区间上的面 积为 ,它近似于高为 ,底为 的小矩形面积,从而得 面积微元为 d [ ( ) ( )]d . A f x g x x = − [ ( ) ( )]d b a A f x g x x = −  分析 [ , ] a b [ , d ] x x x + A f x g x ( ) − ( ) dx [ ( ) ( )] d f x g x x − [ , ] a b 在这个公式中，无论曲线 在x 轴的上方或下方都成立，只 要 在曲线 的下方 即可。 y g x = ( ) y f x = ( ) y f x = ( ) y g x = ( ) a x x dx + b dA

f(x)>0 f(x)<0 8(x)<0 8(x)<0 前页后页结束

前页 后页 结束 f x( ) 0  g x( ) 0  f x( ) 0  g x( ) 0 

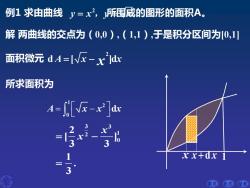
例1求由曲线y=x,围成的图形的面积A。 解两曲线的交点为(0,0)，（1,1)，于是积分区间为0,1] 面积微元dA=V-xdx 所求面积为 A-[-x]dx xx+dx 1 前页后页结束

前页 后页 结束 3 3 2 1 0 2 [ ] 3 3 1 . 3 x = − x = 1 2 0 A x x x = −  d    2 d [ ]d A x x = − x 例1 求由曲线 y x y x = = 2 ， 所围成的图形的面积A。 解 两曲线的交点为（0,0）,（1,1）,于是积分区间为[0,1] 面积微元 所求面积为 x x x + d 1

同理，设函数)，y,（在区间【c,连续， W(y)≤w2y) 求由曲线x=yy,x=y,(y)及直线y=c,y=d(c<d)所 围成的图形的面积！ 在区间【年取小区间 设此区间上的 面积为△则近似于高为dy,底 为y,y)-的矩形面积 (y） 从而得面积微元为 y+dy d4=y2)-4,y)dc. 于是所求面积为 A=[Ψ2(y)-4,(y川dy 前页后页结束

前页 后页 结束 面积为 ,则近似于高为dy,底 同理，设函数 在区间 上连续， 为 的小矩形面积, 在区间 上任取小区间 ,设此小区间上的 求由曲线 及直线 所 围成的图形的面积. 2 1 = −  [ ( ) ( )]d   d c A y y y 1 2   ( ), ( ) y y [ , ] c d 1 2   ( ) ( ) y y  1 2 x y x y = =   ( ), ( ) y c y d c d = =  , ( ) y y + d c d 2  1 ( ) y  ( ) y y [ , d ] y y y + 2 1 d [ ( ) ( )]d . A y y x = −   [ , ] c d A 2 1   ( ) ( ) y y − 于是所求面积为 从而得面积微元为

例2求抛物线2y2与直线 x围成的图形的面积. 解 由 解得交点A(2,-1),B8,2) x=4+2) 取为积分变量，于是，所求面积为： 4=∫2y+4-2yd B(8,2) A(2,-1), 前页后页结来

前页 后页 结束 2 2 1 2 2 3 1 (2 4 2 )d 2 = 4 3 9. A y y y y y y − − = + −   + −     =  解 由 解得交点A(2,-1),B(8,2) 例2 求抛物线 与直线 所围成的图形的面积. 2 2 y x = x y − = 2 4 2 4 2 x y x y  =   = + A(2,-1), B(8,2) 取y为积分变量,于是,所求面积为:

(2)极坐标下平面图形的面积 设曲线的极坐标方程r=r(0),r(0在【a,B]上连续， 且r(0)>0求此曲线与射线0=a,0=B所围成的曲边 扇形的面积. 在区间[a,]上任取一小区间I0,0+d01,设此小区间 上曲边扇形的面积为△A,则△4A近似于半径为r(),中心 角为de的扇形面积， r=r(0) 从而得到面积微元为d4=r2a8, 2 从而可得面积为 0+d9 前页后页结束

前页 后页 结束 且 求此曲线与射线 所围成的曲边 扇形的面积. (2)极坐标下平面图形的面积 设曲线的极坐标方程 r r r = ( ) ( )   ， 在 [ , ]   上连续, r( ) 0       = = ， r r = ( )     r   + d 在区间 上任取一小区间 ,设此小区间 上曲边扇形的面积为 ,则 近似于半径为 ,中心 [ , ]   [ , d ]    + A A r( )  角为 d 的扇形面积, 1 2 d d 2 A r = ， 1 1 2 ( )d . 2 2 A r   =    从而可得面积为 从而得到面积微元为

例3求心形线r=a(1+c0s) 所围成的面积. 解当0从0变到π时，得r=a(1+cosx的图形为上半 部分，心形线所围图形的面积A为极轴上方部分的两倍，即 A-2(+ =a2[(1+2cos9+cos20)d8 2 =82n9+n29l 前页后页结束

前页 后页 结束 π 2 2 0 1 2 (1 cos ) d 2 = +    A a π 2 2 0 = + + (1 2cos cos )d     a π 2 0 3 1 ( 2cos cos2 )d 2 2 = + +     a π 2 0 2 3 1 2sin sin2 2 4 3 π . 2 a a      = + +     = 例3 求心形线 r a = + (1 cos )  所围成的面积. 解 当 从0变到 时,得 的图形为上半 部分,心形线所围图形的面积A为极轴上方部分的两倍,即   r a x = + (1 cos )