《线性代数》课程PPT教学课件（同济第五版）第三章 矩阵的初等变换与线性方程组 第三节 线性方程组的解

第三节线性方程组的解 线性代教

第三节 线性方程组的解

设有n个未知数m个方程的线性方程 0X+0,+.+0.Xn=b, 0,+0a,+.+0.Xn=b2, (3) axtax+.+ax=b 由第二章第哺知3)可以写成向量方程 Ax=b (4 今后线性方程组)与向量方程4)将混同使用而不加区 解 解向量 在名称上不加区别

设有n个未知数m个方程的线性方程 (3) , , 1 1 2 2 , 2 1 1 2 2 2 2 2 1 1 1 1 2 2 1 1        + + + = + + + = + + + = m m m n n m n n n n a x a x a x b a x a x a x b a x a x a x b     (4) 3 Ax = b 由第二章第四节 知（ ）可以写成向量方程 今后线性方程组(3)与向量方程(4)将混同使用而不加区分， 解 解向量 在名称上不加区别

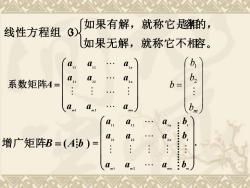
如果有解，就称它的， 线性方程组 6) 如果无解，就称它不镕。 系数矩阵A= b= b 增广矩阵B=(Ab)= N- b

 如果无解，就称它不相容。 如果有解，就称它是相容的， 线性方程组（3）   = m m m nnn a a a a a a a a a A       1 2 2 1 2 2 2 1 1 1 2 1 系数矩阵   = bmbb b 21 增广矩阵B = ( A b ) . 1 2 2 1 2 2 2 2 1 1 1 2 1 1   = m m m n m nn a a a b a a a b a a a b       

、线性方程组有解的判定条件 问题：如何利用系数矩阵A和增广矩阵B的秩， 讨论线性方程组Ax=b的解. 定理趣n元齐次线性方程组nx=b (1)无解的充分必要条件是4)<R(B)=R(A,b): (2)有惟一解的充分必要条件是R(A=R(A,b)=n, (3)有无限多解的充分腰骅是 R()=R(A,b)<n.(n为未知数的个娄

定理3 一、线性方程组有解的判定条件 无解的充分必要条件是R(A)  R(B) = R(A,b)； 有无限多解的充分必要条件是 讨论线性方程组 的解． 如何利用系数矩阵 和增广矩阵 的秩， Ax b A B = 问题： ⑵ ⑴ ⑶ （n为未知数的个数） n 元齐次线性方程组Amn x = b R(A) = R(A,b)  n

证明 (要证充分必要条件，必要性和充分性两 本定理只需证充分铟为 ()中条件的必要怃解→R(A)<R(A,b), (2)中条件的充分性(A)=R(A,b)=n→有惟一解 (3)中条件的充分R(A)=R(A,b)Kn→有无限解 (2),(3)两结论的逆否无解→R(A)<R(A,b) ()中条件的必要性 由此可)，(3)条件中的充分性脑命题就是1) 中条件的必链同理 (2)中条件的必要是(1)3)条件的充分性櫛否命题

证明 (要证充分必要条件，需证必要性和充分性两部分 。 本定理只需证充分性， (1)中条件的必要性: (2)中条件的充分性：R(A) = R(A,b) n有无限多解， (2),(3)两结论的逆否命: (1)中条件的必要性 由此可知(2),(3)条件中的充分性的逆否命题 中条件的必要性. 无解R(A)  R(A,b), (3)中条件的充分性: R(A) =R(A,b ) = n有惟一解， 因为无解R(A)  R(A,b) 就是(1) 同理， (2)中条件的必要性是(1)(3) 条件的充分性的逆否命题

3)中条件的必要恤2)条件的充分性否命题 下面我们来证此定理的分性 首先由所学内容下述结论 方程组Ar气，同解A=方（方程组 增广矩椰=(A,b)之B=(A,(增广矩阵 例如 x1+X2-3x3-x4=1, 对于方程组3x,-x2-3x3+4x4=4, x1+5x2-9x3-8x4=0

(3)中条件的必要性是(1)(2)条件的充分性的逆否命题。 下面我们来证此定理的充分性， 首先由所学内容可得下述结论: 方程组Ax = b, 增广矩阵B = (A,b) Ax = b (方程组) ～ r B = (A,b) ～ ～ ～ ～ ～ (增广矩阵) 同解 例如      + − − = − − + = + − − = 5 9 8 0. 3 3 4 4, 3 1, 1 2 3 4 1 2 3 4 1 2 3 4 x x x x x x x x x x x x 对于方程组

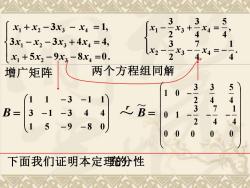
3 3 5 x1+x2-3x3-X4=1, x3+ 2 3x1-X2-3x3+4x4=4, 3 X3 2 一X4 x1+5x2-9x3-8x4=0. 4 增广矩阵 两个方程组同解 3 3 0 5 11-3-11 2 / 4 B= 3-1-3 4 人B= 3 4 01 15 2 -9 -80 00 0 下面我们证明本定理的纷性

     + − − = − − + = + − − = 5 9 8 0. 3 3 4 4, 3 1, 1 2 3 4 1 2 3 4 1 2 3 4 x x x x x x x x x x x x 增广矩阵 B =           − − − − − − 1 5 9 8 0 3 1 3 4 4 1 1 3 1 1 ～ r B =                 − − − − 0 0 0 0 0 4 1 4 7 2 3 0 1 4 5 4 3 2 3 1 0 ～     − − = − . 4 1 4 7 2 3 x2 x3 x4     − + = , 4 5 4 3 2 3 1 3 4 x x x 两个方程组同解 下面我们证明本定理的充分性

设R(A)=r.为叙述方便无妨设=(A,b)的行最简形 b11 bi.n-r d 0 b21 b2.n-r d B 人B= 0 b ,n-r dr 0 0 0 0 d r+1 0 0 0

设R(A) = r.为叙述方便无妨设B = (A,b)的行最简形为                           + − − − 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 1 0 0 1 1 , 2 1 2, 2 1 1 1, 1                         r r r n r r n r n r d b b d b b d b b d B ～ r B ～ =

看0的茹B州则B中的d+1=1, 于是B的第r+1行对应矛盾方翻=1， 故方程4)无解。 (2) 着20的充勋鹅=r=n,则B中的dr+1=0 (或d,+1不出现，且b都不出现 与B对应的方程组是 x=d, x,=d, 故方程4)有惟一解。 x.=d

⑴ 1, 则 B中的 d r + 1 = ～ 于 是B的 第 r + 1行对应矛盾方程0 = 1， ⑵ 则 B中的 d r + 1 = 0 且bij都不出现，  === , 2 2 1 1 xn d n x d x d  故 方 程(4)有惟一解。 ～ ～ 若看(R1()的充分性 A)  R(B), 故方程(4)无解。 ( ), 或dr+1 不出现 若看(R 2 ( )的充分性 A ) = R ( B ) = r = n , 与 B对应的方程组是 ～

(3) 藉来看承的充分性<，则B中的d =0 (或d+1不出现此时对应的方程组为 x1+b11xr+1++b1,n-rxn=1, X2+b21七r+1++b2,m-rxn=2, (⑤) xr+brxr++brn-rxn=dr2 即 x1=-b11x+1-b,n-rxn+1, x2=-b21xr+1-b2,-rxn+2, xr=-br1xr+1-brn-rxn+dr

⑶ 若R(A) = R(A) = r  n, 此 时B对应的方程组为 (5) , , , 1 1 , 2 2 1 1 2, 2 1 1 1 1 1, 1        + + + = + + + = + + + = + − + − + − r r r r n r n r r n r n r n r n x b x b x d x b x b x d x b x b x d     再来看(3)的充分性 则B中的dr+1 = 0 ( ) 或dr+1 不出现 即 (6) , , , 1 1 , 2 2 1 1 2, 2 1 1 1 1 1, 1        = − − − + = − − − + = − − − + + − + − + − r r r r n r n r r n r n r n r n x b x b x d x b x b x d x b x b x d     ～