克拉玛依职业技术学院：《复变函数与积分变换》课程教学授课教案

克拉玛依职业技术学院教案 教案序号： 01课型：理论授课时间：2021-9-3 班级：测控2141班 教材：《复变函数与积分变换》 网络学习条件：安静的环境，网络通畅学生人数：30 教学设备安全情况： 教学安全要求： 一、课题： 第一章复数与复平面 §1-1 复数 二、教学目的 1.理解和掌握复数概念及其四则运算、复数的几何表示； 2熟练掌握复数概念及其四则运算、复数的几何表示 三、教学重点和疑、难点： 重点：(1)复数概念 (2)复数的四则运算(3)复数的几何表示 难点：(1)复数概念 〈2〉复数的四则运算〈3)复数的几何表示. 四。教学过程及教学内容安排 教学内容 时间分配 一、思想教育 10分 二、新课内容 75 (一)复数概念 (二)复数的四则运算 5分 15分 (三)复数的几何表示 55分 三、课堂小结 布置作业 5分

克拉玛依职业技术学院教案 教案序号： 01 课型： 理论 授课时间： 2021-9-3_ 班级： 测控 2141 班 教材： 《复变函数与积分变换》 网络学习条件： 安静的环境，网络通畅 学生人数：_30_ 教学设备安全情况：_ 教学安全要求：_ _ 一、课题： 第一章 复数与复平面 §1-1 复数 二、教学目的： 1. 理解和掌握复数概念及其四则运算、复数的几何表示 ； 2. 熟练掌握复数概念及其四则运算、复数的几何表示. 三、教学重点和疑、难点： 重点：〈1〉复数概念 〈2〉复数的四则运算〈3〉复数的几何表示. 难点：〈1〉复数概念 〈2〉复数的四则运算〈3〉复数的几何表示. 四．教学过程及教学内容安排 教学内 容 时间分配 一、思想教育 二、新课内容 （一）复数概念 （二）复数的四则运算 （三）复数的几何表示 10 分 75 分 5 分 15 分 55 分 三、 课堂小结 布置作业 5 分

容 一、思想教育：复数的产生，数学家华罗庚 二、新课内容： (一)复数的概念：x,y为实数 2=x+y =Re(r)】 特殊： 数 =Im(=) Complex Number 虚数单 纯虚数y≠0) 两个复数相等：设=x+少， =+少2，则=32一=,片= 思考：已知x+i=(2x-)+y,求=x+ 共轭复数(Complex Conjugate):设，=x+y,共轭复数为三=x-%,x的共轭复数为x （二)复数的四则运算：设=x+，32=3+ 加法与减法：1±2=(x±x2)+±)， 乘法：52=(x+x2+%2), 2=-1 特别：2=(x+yx-例）=x2+y 除法：互=+=店+=-伍+=)，0 ++-) 复数的模：：Vx2+y2 共轭复数运算性质：士5=5:)=-三：1H: 2Re()=+;2iIm()= 思考：22=1(：≠0) 例1：计算 I-i 答案：(0- 22 2i3 )5-5-1 案：时 例2：证明等式上，++，-=2+，并对此等式作出几何解释。 (结论：平行四边形的对角线的平方和等于四条边的平方和 (三)复数的几何表示： y(lmaginary Axis) 1、复平面(z平面) z=x+yi →x(Real Axis =x- 2、模与辐角 向量的：模r=O-l:辐角(gumont)记rg;0的辐角不确定

内 容 一、思想教育：复数的产生，数学家华罗庚的 二、新课内容： （一）复数的概念： x, y 为实数 两个复数相等：设 , , 1 1 1 2 2 2 z = x +iy z = x +iy 则 1 2 1 2 1 2 z = z  x = x , y = y 思考：已知 x yi x y i 2 + = (2 −1) + ，求 z = x + yi 共轭复数（Complex Conjugate）：设 1 1 1 z = x +iy ，共轭复数为 1 1 1 z = x −iy . x 的共轭复数为 x （二）复数的四则运算：设 , , 1 1 1 2 2 2 z = x +iy z = x +iy 加法与减法： ( ) ( ), 1 2 1 2 1 2 z  z = x  x +i y  y 乘法: ( )( ), 1 2 z1 z2 = x1 +iy1 x2 +iy2 i = − 特别： 2 2 zz = (x +iy)(x −iy) = x + y 除法： ( )( ) ( )( ) ( )( ) ( ) ( ) , 2 0 2 2 2 2 1 1 2 2 2 2 2 2 1 1 2 2 2 2 1 1 2 1  + + − = + − + − = + + = z x y x iy x iy x iy x iy x iy x iy x iy x iy z z 复数的模： 2 2 | z |= x + y 共轭复数运算性质： _ 2 _ 1 _ 1 2 z  z = z  z ； ( ) _ 2 _ 1 _ 1 2 z z = z z ； _ 2 _ 1 _ 2 1 z z z z =        ； | z|=| z | ； 2Re(z) = z + z;2iIm(z) = z − z 思考： 1( 0) 1  =  − z z z 例 1：计算： i i i i − + − 1 1 (1) 答案： i 2 1 2 3 (1) − − ； i i 2 3 2 3 (2) − + 答案： i 13 12 13 5 (2) − + 3 1 3 3 2 (3) − − −i i i 答案： i 4 5 3 4 1 (3) + 例 2：证明等式 ( ) 2 1 2 2 1 2 2 z1 + z2 + z − z = 2 z + z ，并对此等式作出几何解释。 （结论：平行四边形的对角线的平方和等于四条边的平方和） （三）复数的几何表示： 2、模与辐角 向量的模： r OP z  = = → ；辐角（Argument）记 Argz ；0 的辐角不确定。 x （Real Axis） y (Imaginary Axis） P 1、复平面（ 平面） i z = x +iy 复 数 Complex Number      = = i虚数单位 y z x z Im( ) Re( ) 特殊： 实数 x 纯虚数 yi(y  0) z = x − yi O

辐角主值：记arg:,范围-π0,y>0, 第一、四象限 xx0 第二象限 arctan2-x0.v=0 x正半轴 x0 y正半轴 x=0y<0 y负半轴 arg 复数的三角形式：z=x+yi=r(cos0+isin0):x=rcos0,y=rsin0. 复数的指数形式：z=re 例3：将复数：=1-√31分别化为三角表达式和指数表达式 (==2 cos(- 写+2a)+1sm(-+2ka)2ek=0412) 复平面上任意两点间的距离：与-=V任-x)+0-2尸 3、复数三角表示作乘除法 =(cos0 +isin ),=(cos0,+isin), 乘法：三，·3，=r5[cos(0+0,)+isin(0+0,)】 推广：，=(cos0+isin0)i=12,3 5233=r5[cos(0+0+6)+isim(0+6,+0】 除法：1-[cos(8-,)+i5in(8-,】(≠0) 2、r 例4：化简-V5(cos0+1sn0) (1-i)(cos0-isin0) 答案，co20-+ism2- 乘方：z"=[r(cos+isin8)=r(cosn0+isin ne -1 三、课堂小结： 布置作业：作业： 五.课后小结：

辐角主值：记 arg z ，范围− 0  ， Argz = arg z + 2k(k = 0,1,2, ) 当 z  0 时， z 的辐角主值如下：                  − =  =   =  = −   +       = 0, 0 2 0, 0 2 0, 0 0 0, 0 arctan 0, 0 arctan 0, 0 0, 0 0, 0, arctan arg x y x y x y x y x y x y x y x y x y x y x y z      复数的三角形式： z = x + yi = r(cos +isin) ； x = r cos, y = rsin . 复数的指数形式： i z = re 例 3：将复数 z =1− 3i 分别化为三角表达式和指数表达式。 （ i k i z k i k e       2 3 2 ) 2 3 2 ) sin( 3 2 cos( − + =      = − + + − + (k = 0,1,2, ) ） 复平面上任意两点间的距离： 2 1 2 2 1 2 1 2 z − z = (x − x ) + ( y − y ) 3、复数三角表示作乘除法 设 (cos sin ) 1 1 1 1 z = r +i ， (cos sin ) 2 2 2 2 z = r +i ， 乘法： [cos( ) sin( )] 1 2 = 1 2 1 +2 + 1 +2 z z rr i 推广 zi = ri (cosi +isini ) i =1,2,3 [cos( ) sin( )] 1 2 3 = 1 2 1 +2 +3 + 1 +2 +3 z z z rr i 除法： [cos( ) sin( )] 1 2 1 2 2 1 2 1 =  − + i  − r r z z ( 0) r2  例 4：化简 (1 )(cos sin ) (1 3 )(cos sin )     i i i i − − − + 答案：       − + − ) 12 ) sin(2 12 2 cos(2     i 乘方： z [r(cos isin)] r (cosn isin n) n n n = + = + 例 5：设 n 为正整数，试证明 1 2 1 3 2 1 3 3 1 3 1 = −         − − +         − + n+ n+ i i 三、课堂小结： 本次课重点在于讲复数的概念及四则运算和复数的几何表示。 布置作业：作业： 完成《复变函数与积分变换》学生工作任务单（1） 五．课后小结： 第一、四象限 第二象限 第三象限 x 正半轴 x 负半轴 y 正半轴 y 负半轴 arg z x y z x y arctan O x y arctan O arg z y z x y arctan x

克拉玛依职业技术学院教案 教案序号： 02课型： 理论授课时间：2022-9-5 班级：测控2141班 教材：《复变函数与积分变换》 网络学习条件：安静的环境，网络通畅学生人数：28 教学设备安全情况： 教学安全要求： 一、课题： 第一章 复数与复平面 §1-2 复平面上的点集 二、教学目的： 1.理解和掌握复数的乘除法与开方及复球面的概念 2.。熟练掌握复数的乘除法与开方及复球面的概念。 三、教学重点和疑、难点： 重点：(1)复数的乘除法与开方(2)复球面 难点：(1)复数的乘除法与开方(2)复球面 四.教学过程及教学内容安排 教学内容 时间分配 一、思想教育与复习 10分 二、新课内容 75 (一)复数的乘除法与开方 (二)复球面 0分 25分 三、课堂小结 布置作业 5分

克拉玛依职业技术学院教案 教案序号： 02 课型： 理论 授课时间： 2022- 9 -5 班级： 测控 2141 班 教材： 《复变函数与积分变换》 网络学习条件：安静的环境，网络通畅 学生人数：_28_ 教学设备安全情况：_ 教学安全要求：_ _ 一、课题： 第一章 复数与复平面 §1-2 复平面上的点集 二、教学目的： 1. 理解和掌握复数的乘除法与开方及复球面的概念； 2. 熟练掌握复数的乘除法与开方及复球面的概念。 三、教学重点和疑、难点： 重点：〈1〉复数的乘除法与开方〈2〉复球面 难点：〈1〉复数的乘除法与开方〈2〉复球面 四．教学过程及教学内容安排 教学内 容 时间分配 一、思想教育与复习 二、新课内容 （一） 复数的乘除法与开方 （二） 复球面 10 分 75 分 50 分 25 分 三、 课堂小结 布置作业 5 分

容 一、思想教育：数学家祖冲之 二、新课内容： (一)复数三角表示作乘除法 设：=r(cos6+isin),-2=5(cos8,+isin8),， 乘法 -2=r5lcos8+8,)+isin(8+】 推广-，=r(cos8+isin8)i=1,2,3 253=r5[cos(8+6,+8)+isin(8+8+8】 降法手=c0日-8)+1sm日-816+0) 例1：化简L-V30c0sB+1sn9) (1-i)(cos0-isin0) 答案：co0-+ism(20- 乘方：：”=[r(cos0+isin0)r=r"(cosn0+isinn0) 例2：设n为正整数。试证明-1+5）- =-1 2 +2 (二)复数的开方 设：=(cos0+isin),0=p(cosp+isin)若a=(n>L,neZ),称o为：的n次方 根。记E,)”-p(cosnp+isinno),求方根的运算叫开方。 p=听，：4dg0=0=0+2krk=0t12.) 说明：(1)当k=0,12,n-1时，得n个相异的值。，0,2，0 2）每两个相邻辐角的差为2红 例1：求(1)折 (2)+i 据：601=o0+2n）1m0+2n.=cs2+1sm21k=012. 3 四个根为： nded)

内 容 一、思想教育：数学家祖冲之的 二、新课内容： （一）复数三角表示作乘除法 设 (cos sin ) 1 1 1 1 z = r +i ， (cos sin ) 2 2 2 2 z = r +i ， 乘法： [cos( ) sin( )] 1 2 = 1 2 1 +2 + 1 +2 z z rr i 推广 zi = ri (cosi +isini ) i =1,2,3 [cos( ) sin( )] 1 2 3 = 1 2 1 +2 +3 + 1 +2 +3 z z z rr i 除法： [cos( ) sin( )] 1 2 1 2 2 1 2 1 =  − + i  − r r z z ( 0) r2  例 1：化简 (1 )(cos sin ) (1 3 )(cos sin )     i i i i − − − + 答案：       − + − ) 12 ) sin(2 12 2 cos(2     i 乘方： z [r(cos isin)] r (cosn isin n) n n n = + = + 例 2：设 n 为正整数，试证明 1 2 1 3 2 1 3 3 1 3 1 = −         − − +         − + n+ n+ i i （二）复数的开方 设 z = r(cos +isin) ，  = (cos +isin) 若 z(n 1,n Z) n  =   ,称  为 z 的 n 次方 根。记 n z ，  (cosn isin n) n n = + ，求方根的运算叫开方。 n  = r ，: ( 0, 1, 2, ) 2 =    + = = k n k Arg     说明：（1）当 k = 0,1,2,  ,n−1 时，得 n 个相异的值。 0 1 2 1 , , , ,     n− （2）每两个相邻辐角的差为 n 2 例 1：求（1） 3 1 （2） 4 1+i 解:(1) 1= cos(0+ 2k )+isin(0+ 2k ), | 0,1,2} 3 2 sin 3 2 1 {cos 3 = + k = k i k  , 三个根为： i i 2 3 2 1 , 2 3 2 1 1 , − + − − （2） 2 , 4 2 isin 4 1 2 cos              + +      + = +     i k k        =       + +      + = + 0,1,2,3 4 16 2 sin 4 16 2 1 2 cos 4 8 k k i k i     ， 四个根为：       + 16 sin 16 2 cos 8   i ，       + 16 9 sin 16 9 2 cos 8   i       − 16 15 sin 16 15 2 cos 8   i ,       − 16 7 sin 16 7 2 cos 8   i （三）复球面(Complex Sphere):复平面上加点  后称为扩充复平面(Extended) 模为有限的复数，称为有限复数，除去  的复平面称为有限复平面

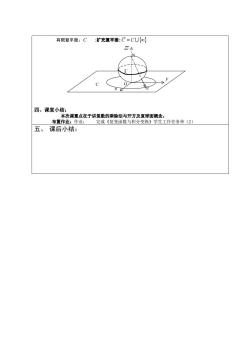
有限复平面：C:扩充复平面：C=CU{o 三A 四、课堂小结： 次课重点在于讲复数的乘除法上 开方及复 布置 作业 五、课后小结：

有限复平面：C ;扩充复平面: C =C 四、课堂小结： 本次课重点在于讲复数的乘除法与开方及复球面概念。 布置作业：作业： 完成《复变函数与积分变换》学生工作任务单（2） 五、 课后小结： C x y Q O N z

克拉玛依职业技术学院教案 教案序号：03课型：理论授课时间：2022-9-19 班级： 测控2141班 教材：《复变函数与积分变换》 网络学习条件：安静的环境，网络通畅学生人数： 29 教学设备安全情况： 教学安全要求： 一、课题： 第一章 复数与复平面 §1-2 复平面上的点集 二、教学目的 1.理解和掌握复平面上的点集的基本概念与平面曲线： 2.熟练掌握复平面上的点集的与平面曲线。 三、教学重点和疑、难点： 重点：(1)复平面上的点集〈2)平面曲线 难点：1〉复平面上的点集(2)平面曲线 四.教学过程及教学内容安排 教学内容 时间分配 一、思想教育与复习 10分 二、新课内容 75分 (一)复平面上的点集 (30分) (一)平面曲线 (25分) (三) 复变函数的概念 (20分) 三、课堂小结 5分 布置作业

克拉玛依职业技术学院教案 教案序号： 03 课型： 理论 授课时间： 2022- 9 -19 班级： 测控 2141 班 教材： 《复变函数与积分变换》 网络学习条件：安静的环境，网络通畅 学生人数：_29_ 教学设备安全情况：_ 教学安全要求：_ _ 一、课题： 第一章 复数与复平面 §1-2 复平面上的点集 二、教学目的： 1. 理解和掌握复平面上的点集的基本概念与平面曲线； 2. 熟练掌握复平面上的点集的与平面曲线。 三、教学重点和疑、难点： 重点：〈1〉复平面上的点集〈2〉平面曲线 难点：〈1〉复平面上的点集 〈2〉平面曲线 四．教学过程及教学内容安排 教学内 容 时间分配 一、思想教育与复习 二、新课内容 （一）复平面上的点集 （二） 平面曲线 （三） 复变函数的概念 10 分 75 分 （30 分） （25 分） （20 分） 三、 课堂小结 布置作业 5 分

内 容 一、思想教育：数学家陈景润 复习：复数的三角形式和指数形式，复数的开方 二、新课内容： 一)复平面上的点地 1、基本概念：的6-领域，记N,(5o),上-0)，的去心6-领域01,Im(e)>0 (3)片I (2)2+≤2+ H<1.Re)s号 0

内 容 一、思想教育：数学家陈景润 复习：复数的三角形式和指数形式，复数的开方 二、新课内容： （一）复平面上的点集 1、基本概念： 0 z 的  −领域，记 ( )0 N z  ， ( 0) z − z0     ， 0 z 的去心  −领域 0  z − z0   内点（Interior Point）:若点集 D 的点 0 z 有一领域全含于 D 内，则称 0 z 为 D 的内点。 开集（Open Set）:若点集 D 的点全为内点，则称 D 为开集。 边界点（Boundary Point）:若在点 0 z 的任意邻域内，同时有属于 D 的点和不属于 D 的点则称 0 z 为 D 的边界点，所有 D 的边界点够成的点集称为 D 的边界，记 D. 余集：平面上不属于点集 D 的点的全体称为 D 的余集。记 c D 。 闭集：开集的余集称为闭集。 一个集合是开集  集合中的每一点都是它的内点。 孤立点：设 , z0 D 若在 0 z 的某一领域内除 0 z 外不含 D 的其他点，则称 0 z 为 D 的孤立点。 有界集：若有正数 M ,对于点集 D 内的点 z ，都满足 z  M ,即若 D 全含于某一圆内，则称 D 为有界集，否则就称 D 为无界集。 连通：如果开集 S 内的任意一对点 1 2 z ,z 都能被含于 S 内的折线连接起来，则称 S 是连通的。 区域（Domain）：若非空点集 D 即是开集又具有连通性，则 D 称为区域。 闭区域：区域 D + D= D 例 1：指出下列点集是否为区域、闭区域；是有界集还是无界集？ （1） z 平面上以圆点为圆心， R 为半径的圆形区域。 z  R ，闭区域 z  R （2） z 1,Im(z)  0 （3） 1 2 y  Im(z)  y （4） r  z  R 连续曲线(Continuous Curve)：如果曲线 :z = x(t) +iy(t) (  t  ) 的实部与虚部均为 t 的连续函数，则曲线  为连续曲线。连续曲线没有重点，称为简单曲线。当 z() = z() 连续曲线 称为简单闭曲线。 光滑曲线：如果连续曲线  =   : ( )( ) z z t t   在给定区间上存在连续的 x t y t   ( ), ( ) ，且二者 不同时为 0，即曲线  上每点均有切线且切线方向是连续变化的，则称这种曲线为光滑曲线。 逐段光滑曲线：由有限段光滑曲线连接而成的连续曲线称为逐段光滑曲线。 约当定理：简单闭曲线把扩充复平面分成两个部分，一部分不含  的点集，称为该曲线的内 部；另一部分是含  的点集，称为该曲线的外部；这两个区域都以已给的简单闭曲线作为边界。 单连通区域：在复平面上，如果区域 D 内任意一条简单曲线的内部都含于区域 D 内，则称 D 为单连通区域。否则就称为多连通区域。 例 1：指出下列不等式中点 z 在怎样的点集内变动？它们是单连通区域吗？是否有界？ 2 1 (1) Re(z)  (2) z + i  2 + i 2 1 (3) z 1, Re(z)  x x y o x y O 2 1 y O

三、课堂小结：本次课重点在于讲复平面上的点集。 布置作业： 完成《复变函数与积分变换》学生工作任务单(4) 五.课后小结

三、课堂小结：本次课重点在于讲复平面上的点集。 布置作业： 完成《复变函数与积分变换》学生工作任务单（4） 五．课后小结：

克拉玛依职业技术学院教案 教案序号： 04课型： 理论授课时间：2022-9-26 班级：测控2141班 教材：《复变函数与积分变换》 网络学习条件：安静的环境，网络通畅学生人数：26 教学设备安全情况： 教学安全要求： 一、课题： 第二章解析函数 §2-1复变函数的概念极限与连续 二、教学目的： 1.理解和掌握复变函数的概念、极限与连续的概念、解析函数的概念 2。熟练掌握复变函数的概念、极限与连续的概念、解析函数的概念。 三、教学重点和疑、难点： 重点：(1)复变函数的概念、极限与连续的概念： (2》解析函数的概念 难点：1)解析函数的概念 四.教学过程及教学内容安排 教学内容 时间分配 思想教育与复习 三、新为 10分 75分 (一）复变函数的概念 (10分) 30分〉 (35分) 三、课堂小结 5分 布置作业

克拉玛依职业技术学院教案 教案序号： 04 课型： 理论 授课时间： 2022-9 -26 班级： 测控 2141 班 教材： 《复变函数与积分变换》 网络学习条件：安静的环境，网络通畅 学生人数：_26_ 教学设备安全情况：_ 教学安全要求：_ _ 一、课题： 第二章 解析函数 §2-1 复变函数的概念 极限与连续 二、教学目的： 1. 理解和掌握复变函数的概念、极限与连续的概念、解析函数的概念。 2. 熟练掌握复变函数的概念、极限与连续的概念、解析函数的概念。 三、教学重点和疑、难点： 重点：〈1〉复变函数的概念、极限与连续的概念； 〈2〉解析函数的概念。 难点：〈1〉解析函数的概念 四．教学过程及教学内容安排 教学内 容 时间分配 一、 思想教育与复习 二、新课内容 （一）复变函数的概念 （二）复变函数的极限与连续 （三）解析函数 10 分 75 分 （10 分） （30 分） （35 分） 三、 课堂小结 布置作业 5 分