《线性代数》课程PPT教学课件（同济第五版）第一章 行列式 第五节 行列式性质

第五节行列式性质 线性代教

第五节 行列式性质

行列式的性质 记 l12 41T D 0h2 021 D 4m2 m 行列式D'称为行列式D的转置行列式. 性质1 行列式与它的转置行列式相等

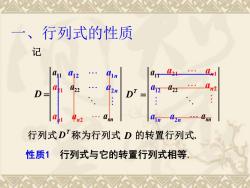
一、行列式的性质 性质1 行列式与它的转置行列式相等. 行列式 称为行列式 的转置行列式. T D D 记 nn a a a  22 11    n n a a a 2 12 1   1 2 21 n n a a a D =    2 21 1 n n a a a   n n a a a 1 2 12 = T D nn a a a  22 11

证明 记D=det(a,的转置行列式 bu b12 b22 bn2 .bnn 即b=a(,j=1,2,n,按定义 DT=∑(1ヅhnb,.bm,=∑(1an14p2.apn 又因为行列式D可表示为 D=∑(1yap,14ph2.pn

证明 记 D = det(aij)的转置行列式, 1 2 21 22 2 11 12 1 n n nn n n T b b b b b b b b b D     = b a (i, j 1,2, ,n), 即 ij = ij =  按定义 ( 1) ( 1) . =  − 1 1 2 2 =  − p11 p2 2 p n t p p np T t n n D b b b a a a 又因为行列式D可表示为 ( 1) . =  − p11 p2 2 p n t n D a a a

故」 D=D". 证毕 说明行列式中行与列具有同等的地位，因此行列 式的性质凡是对行成立的对列也同样成立， 性质2】 互换行列式的两行（列），行列式变号， 第行（列)与第j行（列）交换记为分r(c:分c) 证明 设行列式 bu D1= b22 b20 bn2 是由行列式D=det(a:)变换i,j两行得到的

故 . T D = D 证毕 性质2 互换行列式的两行（列）,行列式变号. 证明 设行列式 , 1 2 21 22 2 11 12 1 1 n n nn n n b b b b b b b b b D     = 说明 行列式中行与列具有同等的地位,因此行列 式的性质凡是对行成立的对列也同样成立. 是由行列式 D = det(aij) 变换 两行得到的, i, j 第i行（列）与第j行（列）交换记为 ( ) i j i j r  r c  c

即当k≠i,j时，bp=kp；当k=i,j时， bp=ap’bp=ap, 于是 D,=∑(-lbn.bp,bpbp. =∑(1an.,.0p,.m. =∑(1ya.0p,aim0p.’， 其中1.i.j.n为自然排列 为排列p.P,.p.pn的逆序数 设排列p1.Pp:.p.pn的逆序数为，则有

于是 ( ) i j npn p ip jp t D b b b b 1 1 1 =  − 1 ( ) i j npn p ip jp t a a a a 1 1 =  − 1 ( 1) , 1 1 j i npn p ip jp t =  − a a a a 其中1i jn为自然排列, . t为排列 p1 pi pj pn 的逆序数 , 1 1 p p p p t 设排列  i  j  n 的逆序数为 则有 即当 时, k  i, j ; bkp = akp 当 k i j 时, = , , , bip = ajp bjp = aip

(-1y=-(-1, 故D=-∑(1少4n,0p,.am.0. =-D证毕 例如 17 5 17 5 17 5 715 2=-3 5 1←→C2 6 6 8 66 2 三一 6 6 2. 3 5 8 6 62 35 8 5 3 8 推论 如果行列式有两行（列）完全相同，则 此行列式为零 证明互换相同的两行，有D=一D, .D=0

例如 推论 如果行列式有两行（列）完全相同，则 此行列式为零. 证明 互换相同的两行，有  D = 0. D = −D, ( 1) ( 1) , 1 t t − = − − 故 ( 1) . 1 1 D1 a1 a a a D j i npn p ip jp t = − −    = − 证毕 , 1 7 5 1 7 5 6 6 2 = − 3 5 8 . 8 2 5 8 2 5 = − 3 6 1 5 6 7 5 6 7 3 6 1 6 6 2 3 5 8 2 3 r  r 1 2 c  c

性质3行列式的某一行（列） 中所有的元素都 乘以同一数k，等于用数k乘此行列式 11 L12 11 L12 n kai kai2 kain =k ai Qi2 Qin nn 第i行（或列）乘以k,记作r×k(或C,×k) 推论行列式的某一行（列)中所有元素的公因 子可以提到行列式符号的外面. 第行（或列）提出公因子k,记作÷k(或C,÷k)

性质3 行列式的某一行（列）中所有的元素都 乘以同一数 k ，等于用数 k 乘此行列式. n n nn i i in n a a a ka ka ka a a a      1 2 1 2 11 12 1 n n nn i i in n a a a a a a a a a k      1 2 1 2 11 12 1 = 推论 行列式的某一行（列）中所有元素的公因 子可以提到行列式符号的外面． 第i行(或列）乘以k,记作 r k( c k). i  或 i  第i行(或列）提出公因子k,记作 r k( c k). i  或 i 

举例说明性质3及其推论 2 23 23 0 -1 -1 4 二0 -1 1 2 -3 4 -3 -3 4 8 -12 16 (一个数 对列也有相同的运算，同学们可以试一试。 实际计算时常用推论的形式，比如 1 2 3 ”÷4 2 3 0 0 -1 8 -1216 2 -3 第三行有公因子4

举例说明性质3及其推论 , 2 3 4 0 1 1 1 2 3 − − (一个数) 2 3 4 0 1 1 1 2 3 − 4 − = = 2 3 4 0 4 4 1 2 3 − − 8 12 16 0 1 1 1 2 3 − − 对列也有相同的运算，同学们可以试一试。 实际计算时常用推论的形式，比如 8 12 16 0 1 1 1 2 3 − − r 3  4 4 2 3 4 0 1 1 1 2 3 − − 第三行有公因子4

性质4 行列式中如果有两行（列)元素成比 例，则此行列式为零. 证明 11 L12 n 12 。 n 1 ai2 迎 u Ai2 。· in K =0. kai kai2 KQin ai Ai2 in An2 (nl (n2 a nn

性质４ 行列式中如果有两行（列）元素成比 例，则此行列式为零． 证明 n n nn i i in i i in n a a a ka ka ka a a a a a a        1 2 1 2 1 2 11 12 1 n n nn i i in i i in n a a a a a a a a a a a a k        1 2 1 2 1 2 11 12 1 = = 0

性质5 若行列式的某一列（行）的元素都是两 数之和. 11 L12 ·. (av ali) in 例如 D 021 L22 (azi+azi) An2 (ani+a) (nn 则D等于下列两个行列式之和： 11 Avi .1n L11 .n D= L21 Azi .·l2n L21 d .l2n ni i .Qnn

性质5 若行列式的某一列（行）的元素都是两 数之和. n n ni ni nn i i n i i n a a a a a a a a a a a a a a a D           ( ) ( ) ( ) 1 2 2 1 2 2 2 2 2 1 1 1 2 1 1 1 +  +  +  = 则D等于下列两个行列式之和： n ni nn i n i n n ni nn i n i n a a a a a a a a a a a a a a a a a a D                        = + 1 2 1 2 2 1 1 1 1 1 2 1 2 2 1 1 1 1 例如