《线性代数》课程PPT教学课件（同济第五版）第二章 矩阵及其运算 第四节 矩阵的分块法

第四节矩阵的分块法 一、 矩阵的分块 二、分块矩阵的运算法则 三、小结 上一项不页返向首项

第四节 矩阵的分块法 一、矩阵的分块 二、分块矩阵的运算法则 三、小结 上一页 下一页 返回首页

一、矩阵的分块 对于行数和列数较高的矩阵A,为了 简化运算，经常采用分块法，使大矩阵的 运算化成小矩阵的运算.具体做法是：将 矩阵A用若干条纵线和横线分成许多个小 矩阵，每一个小矩阵称为A的子块，以子 块为元素的形式上的矩阵为分块矩阵： 看下面的例子 上一页入不页返回首页

一、矩阵的分块 上一页 下一页 返回首页 对于行数和列数较高的矩阵 A ，为了 简化运算，经常采用分块法，使大矩阵的 运算化成小矩阵的运算.具体做法是：将 矩阵A用若干条纵线和横线分成许多个小 矩阵，每一个小矩阵称为A的子块，以子 块为元素的形式上的矩阵为分块矩阵. 看下面的例子

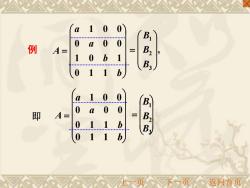
a 10 0 0 a 0 0 B 例 A= 1 b 0 1 B: 11 b 10 0 mmunnnaennmmunaunaunsneesuMMan B 即 0a0 0 A= 011b 011 b 上一页不页返回首页

, 3 2 1           = B B B               = b b a a A 0 1 1 1 0 1 0 0 0 1 0 0 例               A = a 1 0 0 b a 0 1 1 0 0 0 0 1 1 b           = B1 B2 B3 即 上一页 下一页 返回首页

0 0 0 a 0 0 C2 A= 1 0 b 1 0 1 1 b a 1 0 0 即 0 0 A= 0 C 0 b 1 0 b 上一页G入不页返向首页

              = b b a a A 0 1 1 1 0 1 0 0 0 1 0 0 , 3 4 1 2       = C C C C       =               A = a 1 C1 0 0 C2 0 1 1 0 0 a C3 b b 1 1 0 0 C4 即 上一页 下一页 返回首页

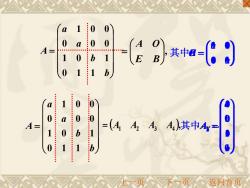
a 1 0 0 0 0 0 A 1 0 b 1 任g*aG9 0 1 1 b 1 0 0 a 0 A= 1 0 b 0 1 1 01.5: =(44,AA)其中4 上一页入不页返回首页

,      = E B A O ( ), = A1 A2 A3 A4               = b b a a A 0 1 1 1 0 1 0 0 0 1 0 0               = b b a a A 0 1 1 1 0 1 0 0 0 1 0 0       = a a A 0 1 其中       = b b B 1 1       = 0 1 1 0 E       = 0 0 0 0 O               = 0 1 0 1 a 其中A               = 1 0 1 2 a A               = 1 0 0 3 b A               = b A 1 0 0 4 上一页 下一页 返回首页

二、分块矩阵的运算规则 (1)设矩阵A与B的行数相同，列数相同，采用 相同的分块法，有 A如 A A- B= A B 其中A,与B的行数相同，列数相同，那末 A1+B1 A1,+B1 4+B= 人A1+B1. A+Bs 上一页G不页返向首页

( ) 相同的分块法 有 设矩阵 与 的行数相同 列数相同 采用 , 1 A B , , 其中Aij与Bij的行数相同,列数相同,那末 . 1 1 1 1 1 1 1 1           + + + + + = s s sr sr r r A B A B A B A B A B     二、分块矩阵的运算规则           =           = s sr r s sr r B B B B B A A A A A         1 1 1 1 1 1 1 1 , 上一页 下一页 返回首页

·Ar (2)设A= ,2为数，那末 A A 2A11 AAir 几A= MA. 入上一页不页返回首项

(2)设 , 为数,那末 1 1 1 1            = s sr r A A A A A     . 1 1 1 1           = s sr r A A A A A          上一页 下一页 返回首页

2 3 例九=2， A= 3 2 1 4 5 6 12 3 4- 412 Au 32 A42= 1 421=(45) A22=(6） 2A1 2A12 1×2 2×23×2 4 4 2A212A22 3×2 2×21×2 64 2 4×25×26×2 810 12 下页返回首页

例           = 4 5 6 3 2 1 1 2 3  = 2, A 2 2 2 2           = 4 5 6 3 2 1 1 2 3 2 . 8 10 12 6 4 2 4 4 6           上一页 下一页 返回首页         = 21 22 11 12 A A A A A         = 3 2 1 2 A11         = 1 3 A12 (4 5) A21 = (6) A22 = A = 21 11 A A 22 12 A A         2 2 2 2 2 2 2 2 2 =

3)设A为mx矩阵B为l×n矩阵，分块成 An B11 。 A八 B 其中41，A2,A的列数分别等于B,B2,B。 的行数，那末 C11 AB= 其中C=∑AkB(=1,.,5j=1,） 入上页入不页返同首页

(3)设A为ml矩阵,B为l n矩阵,分块成 , , 1 1 1 1 1 1 1 1           =           = t tr r s st t B B B B B A A A A A         的行数 那末 其中 的列数分别等于 , , , , , , , Ai1 Ai2  Ai t B1 j B2 j  Bt j           = s sr r C C C C AB     1 11 1 ( 1, , ; 1, , ). 1 C A B i s j r k j t k i j =  i k =  =  = 其 中 上一页 下一页 返回首页

(4)设A= 则AT= A (S)设A为n阶矩阵，若A的分块矩阵只有在主对角线 上有非零子块，其余子块都为零矩阵，且非零子块都 是方阵即 A= 其中A(i=1,2,.S)都是方阵，那么称A为分块对角 矩阵 入上一页不页返向首页

( ) 是方阵 即 上有非零子块 其余子块都为零矩阵 且非零子块都 设 为 阶矩阵 若 的分块矩阵只有在主对角线 . , , 5 A n , A , 2 1   = As A A A  O O (4) , 1 1   = Asr A A     设 A 1 r A s 1 T A s 1 T A 1 r . 11   = T sr T T A A A     则 上一页 下一页 返回首页 A (i s) 其中 i =1,2, 都是方阵，那么称 A 为分块对角 矩阵