《线性代数》课程PPT教学课件（同济第五版）第三章 矩阵的初等变换与线性方程组（习题课）

第三章习题课 线性代教

第三章 习题课

本章主要概念 初等行（列）变换， 二、矩阵的行（列）等价及等价， 三、行阶梯矩阵， 行最简形矩阵， 四、矩阵的子式，最高阶非零子式 矩阵的秩， 五、矩阵秩的一些基本性质， 六、关于方程组AX=b解的结论， 七、关于方程组AX=0解的结论

一、初等行（列）变换， 四、矩阵的子式，最高阶非零子式， 二、矩阵的行（列）等价及等价， 三、行阶梯矩阵，行最简形矩阵， 本章主要概念 矩阵的秩， 五、矩阵秩的一些基本性质， 六、关于方程组AX=b解的结论， 七、关于方程组AX=0解的结论

典型题型 求矩阵的秩 求矩阵的一个最高阶非零子式 求逆矩阵的初等变换法 三、解矩阵方程的初等变换法 四、求解线性方程组

一、求矩阵的秩 四、求解线性方程组 二、求逆矩阵的初等变换法 三、解矩阵方程的初等变换法 典 型 题 型 求矩阵的一个最高阶非零子式

一、 求矩阵的秩 求矩阵的秩有下列基本方法 (1)计算矩阵的各阶子式从阶数最高的子式开始， 找到不等于零的子式中阶数最大的一个子式，则 则这个子式的阶数就是矩阵的秩. (2)用初等变换.即用矩阵的初等行（或列）变换 把所给矩阵化为阶梯形矩阵，由于阶梯形矩阵的秩 就是其非零行（或列）的个数，而初等变换不改变 矩阵的秩，所以化得的阶梯形矩阵中非零行（或列 的个数就是原矩阵的秩

求矩阵的秩有下列基本方法 （１）计算矩阵的各阶子式， 一、求矩阵的秩 从阶数最高的子式开始， 找到不等于零的子式中阶数最大的一个子式，则 则这个子式的阶数就是矩阵的秩． （２）用初等变换．即用矩阵的初等行（或列）变换， 把所给矩阵化为阶梯形矩阵，由于阶梯形矩阵的秩 就是其非零行（或列）的个数，而初等变换不改变 矩阵的秩，所以化得的阶梯形矩阵中非零行（或列） 的个数就是原矩阵的秩．

第一种方法当矩阵的行数与列数较高时，计 算量很大， 第二种方法则较为简单实用. 例1 求下列矩阵的秩，并求它的一个最高罹式： 2 0 6 2 10 A= 1 11 3 6 16 -19 -7-14 -34 解对A施行初等行变换化为阶梯形矩阵

第一种方法当矩阵的行数与列数较高时，计 算量很大， 第二种方法则较为简单实用． 例１ 求下列矩阵的秩， . 1 19 7 14 34 1 11 3 6 16 0 6 2 4 10 1 2 0 0 1               − − − − A = 并求它的一个最高阶非零子式。 解 对 A 施行初等行变换化为阶梯形矩阵

2 0 0 1 0 6 2 10 A= 1 11 3 6 16 化知 -19 -7 -14 -34 1 2 0 0 1 0 6 2 4 10 0 9 3 6 15 0-21 -7-14 -35

              − − − − = 1 19 7 14 34 1 11 3 6 16 0 6 2 4 10 1 2 0 0 1 A           0 − 21 − 7 −14 − 35 0 9 3 6 15 0 6 2 4 10 1 2 0 0 1 ～ r 化为0

2 0 0 2 01 0 6 2 4 10 r 0 3 125 =B 0 9 3 6 15 0 0 0 00 0 -21 -7 -14 -35 0 0 00 因此，R(A)=R(B)=2. 注意在求矩阵的秩时，初等行、列变换可 以同时兼用，但一般多用初等行变换把矩阵化成 阶梯形

              0 0 0 0 0 0 0 0 0 0 0 3 1 2 5 1 2 0 0 1 ~ 因此,R(A) = R(B) = 2. 注意 在求矩阵的秩时，初等行、列变换可 以同时兼用，但一般多用初等行变换把矩阵化成 阶梯形． r = B           0 − 21 − 7 −14 − 35 0 9 3 6 15 0 6 2 4 10 1 2 0 0 1

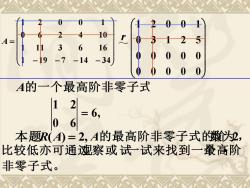
10 5 11 3 16 9 7 -14 -34 A的一个最高阶非零子式 1 2 06 本题R(A)=2,A的最高阶非零子式嫩， 比较低亦可通邈察或试一试来找到一最高阶 非零子式

              − − − − = 1 19 7 14 34 1 11 3 6 16 0 6 2 4 10 1 2 0 0 1 A ～ r               0 0 0 0 0 0 0 0 0 0 0 3 1 2 5 1 2 0 0 1 A的一个最高阶非零子式 0 6 1 2 = 6, 本题R(A) = 2, A的最高阶非零子式的阶数 为2， 比较低亦可通过观察或试一试来找到一个最高阶• 非零子式

例2设矩阵 -2 0 2 -6 -1 A 的秩。 3 2 7 1 -1 -6 -1 b 解 1 1 -2 3 0 1 1 -23 0 2 1 -6 4 -1 0 -1 -2 -2-1 A= 3 2 a 7 -1 0 -1 a+6 -2-1 -1 -6 -1 b 0-2 -4 -4 b 1 -2 3 0 (1)当a=-8,b=-2时，R()=2 (2) 当a=-8,b≠-2时R()=3 0 -1 -2 -2 -1 0 0 (3) 当a≠-8，b=-2时，R(A)=3 0 a+8 0 (4) 当a≠-8，b≠-2时，R(A)=4 0 0 0 0 b+2

例 2 设矩阵   − − − − − − − = b a A 1 1 6 1 3 2 7 1 2 1 6 4 1 1 1 2 3 0 的秩。 解   − − − − − − − = b a A 1 1 6 1 3 2 7 1 2 1 6 4 1 1 1 2 3 0 ～ r   − − − − + − − − − − − − b a 0 2 4 4 0 1 6 2 1 0 1 2 2 1 1 1 2 3 0 ～r   + + − − − − − 0 0 0 0 2 0 0 8 0 0 0 1 2 2 1 1 1 2 3 0 b a ⑴ 当 a = − 8 , b = − 2时， R ( A ) = 2 ⑵ 当 a = − 8 , b  − 2 时 R ( A ) = 3 ⑶ 当 a  − 8 , b = − 2 时, R ( A ) = 3 ⑷ 当 a  − 8 , b  − 2 时, R ( A ) = 4

二、求逆矩阵的初等变换法 要求可逆矩阵A的逆矩阵，只需对分块矩阵 (AE)施行初等行变换，当把A变成E时，原来的E就 变成了A1. 或者对分块矩阵 施行初等列变换，当把A 变成E时，原来的E就变成了A1

. ( ) , , , 1 A A E A E E A 变成了 − 施行初等行变换 当把 变成 时 原来的 就 要求可逆矩阵 的逆矩阵 只需对分块矩阵 , . , 1 E E A A E A −       变成 时 原来的 就变成了 或者对分块矩阵 施行初等列变换 当把 二、求逆矩阵的初等变换法