《经济数学基础》课程PPT教学课件（微积分）第3章 中值定理、导数应用

第3章中值定理、导数应用 3.1中值定理 3.2洛必达法则 3.3函数的单调性与极值 3.4函数图形的描绘 3.6导数在经济中的应用 结束

3.1 中值定理 3.2 洛必达法则 3.3 函数的单调性与极值 3.4 函数图形的描绘 3.6 导数在经济中的应用 结束 第3章 中值定理、导数应用

3.1.1 罗尔定理 定理1设函数f(x)满足下列条件 (1)在闭区间[a,b]上连续； (2)在开区间(a,b)内可导； (3)f(a)=f(b) 则在内至少存在一点5， 使得f()=0 前页后页结束

前页 后页 结束 定理1 设函数 f (x) 满足下列条件 (3) f (a) = f (b) (1) 在闭区间 [a,b] 上连续； (2) 在开区间 (a,b) 内可导; 则在内至少存在一点  ，  3.1.1 罗尔定理 a b 使得 f () = 0

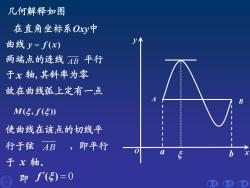
几何解释如图 在直角坐标系Oxy中 曲线y=f(x) 两端，点的连线AB平行 于x轴，其斜率为零 故在曲线孤上定有一点 M(5,f(5) 使曲线在该点的切线平 行于弦AB,即平行 b 于x轴。 即f'(5)=0 前页后页结来

前页 后页 结束  几何解释如图 A B a b 在直角坐标系Oxy 中 曲线 两端点的连线 平行 于x 轴,其斜率为零 y f x = ( ) AB 故在曲线弧上定有一点 使曲线在该点的切线平 行于弦 ，即平行 于 轴。 AB M f ( , ( ))  x f ( )  = 0 O x y 即

3.1.2 拉格朗日中值定理 定理2 设函数f(x)满足下列条件 (1)在闭区间【a,b] 上连续； (2)在开区间 (a,b) 内可导； 则在区间(a,b)内至少存在 一点专，使得 M J-10@ b-a y=f(x) 前页后页结束

前页 后页 结束 则在区间 (a,b) 内至少存在 (1) 在闭区间 [a,b] 上连续； (2) 在开区间 (a,b) 内可导； 定理2 设函数 f (x) 满足下列条件 y = f (x) M A B a  b T ( ) ( ) ( ) f b f a f b a  −  = − 一点  ，使得 3.1.2 拉格朗日中值定理

如图 在直角坐标系Oxy 曲线y=f(x)处处有不垂直 于x轴的切线 端，点连线AB的斜率为 f(b)-f() b-a M R 所以定理实际是说存在 =f(x) 点5，使曲线在该点的 切线T平行于弦AB。 即 e f()=I(b)-f(a) b-a 前页后页结来

前页 后页 结束 曲线 处处有不垂直 于 轴的切线 如图 在直角坐标系Oxy y f x = ( ) x 端点连线AB的斜率为 f b f a ( ) ( ) b a − − 所以定理实际是说存在 点 ，使曲线在该点的 切线T平行于弦AB。  y f x = ( ) M A B a  b T o x y ( ) ( ) ( ) f b f a f b a  −  = − 即

3.1.3 柯西中值定理 定理3 Cauchy中值定理 设函数f(x)与g(x)满足如下条件： 1.在闭区间【a,b]上连续； 2.在开区间(a,b)内可导， 则在区间(a,b)内定有点5 使得 f'(5)_f(b)-f(a g'(5) 3(b)-g(a) 前页后页结束

前页 后页 结束 2.在开区间 (a,b) 内可导， 1.在闭区间 [a,b] 上连续； 定理3 Cauchy中值定理 则在区间 (a,b) 内定有点  ( ) ( ) ( ) ( ) ( ) ( ) g b g a f b f a g f − − =     使得 3.1.3 柯西中值定理 设函数 f x( ) 与 g(x) 满足如下条件：

三个中值定理的关系 Ro11e定理是Lagrange定理的特例： 在Lagrange中值定理中如果f(b)-f(a 则Lagrange中值定理变成Ro1le定理； Cauchy定量是Lagrange定理的推广 在Cauchy中值定理中如果g(x)=x, 则Cauchy化为Lagrange中值定理。 前页后页结束

前页 后页 结束 Rolle定理是Lagrange定理的特例: 在Lagrange中值定理中如果 则Lagrange中值定理变成Rolle定理； Cauchy定量是Lagrange定理的推广 在Cauchy中值定理中如果 ， 则Cauchy化为Lagrange中值定理。 f (b) − f (a) g(x) = x 三个中值定理的关系

3.2洛必达法则 如果在某极限过程下，函数f(x)与g心)同时趋于零或 者同时趋于无穷大，通常把四的极限称为未定式的极 g(x) 限，洛必达法则就是解决这类极限的工具。 一般分为三种类型讨论： 1. 型不定式 00 2. 型不定式。 3.其它型不定式 前页后页结束

前页 后页 结束 如果在某极限过程下,函数f ( x)与g(x)同时趋于零或 者同时趋于无穷大，通常把 的极限称为未定式的极 限，洛必达法则就是解决这类极限的工具。 一般分为三种类型讨论： ( ) ( ) g x f x 3.2 洛必达法则 0 0 1． 型不定式   2． 型不定式． 3．其它型不定式

型未定式 定理1 设函数与在的某空心邻域内有定义，且 满足如下条件： 1) lim f(x)=limg(x)=0 (2)f'(x)和g(x)在该邻域内都存在且 g'(x)≠0； (3) lim f'(x) 存在 （或为 x→a g'(x) 则 lim f(x) lim f(x) →g(x) x-a g'(x) 前页后页结束

前页 后页 结束 定理1 设函数与在的某空心邻域内有定义，且 满足如下条件： 0 0 (1) lim ( ) = lim ( ) = 0 → → f x g x x a x a (2) f (x)和 g (x) 在该邻域内都存在， 且 g (x)  0 ; . ( ) ( ) lim ( ) ( ) lim g x f x g x f x x a x a   = → → 则 （ ）   → ( ) ( ) (3) lim g x f x x a 存在 或为 1． 型未定式．

例1求lim (1+x)2-1 (0为任意实数） x->0 x 解 lim (1+x)°-1 lim a+x”=a x→0 x x2 1 例2求 In(1+x) lim x>0 In(1+x) 解 lim lim 1+x x→0 x2 x-→0 2.x li =00 x-→02x(1+x) 前页后页结束

前页 后页 结束 例1 求 （ 为任意实数） x x x (1 ) 1 lim 0 + − →      = + = + − − → → 1 (1 ) lim (1 ) 1 lim 1 0 2 a x x x 解 x x 例2 求 2 0 ln(1 ) lim x x x + → x x x x x x 2 1 1 lim ln(1 ) lim 0 2 0 + = + 解 → → =  + = → 2 (1 ) 1 lim x 0 x x