同济大学：《复变函数和积分变换》课程教学资源（PPT课件讲稿）2-5-Cauchy型积分公式

01 Cauchy-Goursat公式 目录》 02 Cauchy积分公式 CONTENTS 03 Cauchy高阶导数公式

01 Cauchy-Goursat公式 目 录 CONTENTS 02 Cauchy 积分公式 03 Cauchy 高阶导数公式

01 PART Cauchy-Goursat公式

Cauchy-Goursat 公式 01 PART

Cauchy-Goursat公式 定理设D为有界区域，其边界∂D由有限条互不相交的逐段光滑的简 单闭曲线构成，函数f在D内解析并连续到边界，则 f(z)dz=0, JaD 这里0D取正向. 推论若函数f在单连通区域内解析，则f在该区域内的复积分与路径 无关，从而f在该区域内存在原函数. 证明因单连通区域内的任何一条简单闭曲线，其内部区域必包含于该单 连通区域内，故由Cauchy-Goursat公式，f沿该区域内任何闭曲线 的积分为零，从而结论成立·

Cauchy-Goursat 公式 定理 设 𝐷 为有界区域，其边界 𝜕𝐷 由有限条互不相交的逐段光滑的简 单闭曲线构成，函数 𝑓 在 𝐷 内解析并连续到边界，则 න 𝜕𝐷 𝑓 𝑧 d𝑧 = 0， 这里 𝜕𝐷 取正向． 推论 若函数 𝑓 在单连通区域内解析，则 𝑓 在该区域内的复积分与路径 无关，从而 𝑓 在该区域内存在原函数． 证明 因单连通区域内的任何一条简单闭曲线，其内部区域必包含于该单 连通区域内，故由 Cauchy-Goursat 公式， 𝑓 沿该区域内任何闭曲线 的积分为零，从而结论成立．

注解 注若f(z)的导数连续，则根据Green公式以及Cauchy-Riemann方 程，有 nFro出=ad-时+itr+ad ap aD =-厂a,+owa+ia-d=0. Goursat证明了导数连续的条件是不需要的，该证明超出本课程范围， 略去

注解 注 若 𝑓 𝑧 的导数连续，则根据 Green 公式以及 Cauchy-Riemann 方 程，有 න 𝜕𝐷 𝑓 𝑧 d𝑧 = න 𝜕𝐷 𝑢d𝑥 − 𝑣d𝑦 + 𝑖 න 𝜕𝐷 𝑣d𝑥 + 𝑢d𝑦 = − න 𝐷 (𝑢𝑦+𝑣𝑥)d𝑥d𝑦 + 𝑖 න 𝐷 𝑢𝑥 − 𝑣𝑦 d𝑥d𝑦 = 0． Goursat 证明了导数连续的条件是不需要的，该证明超出本课程范围， 略去．

02 PART Cauchy积分公式

Cauchy 积分公式 02 PART

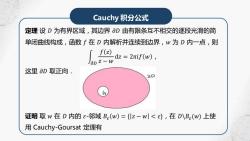
Cauchy积分公式 定理设D为有界区域，其边界∂D由有限条互不相交的逐段光滑的简 单闭曲线构成，函数f在D内解析并连续到边界，w为D内一点，则 f(2) dz=2πif(w), Jad Z-w 这里∂D取正向· D 证明取w在D内的ε-邻域Be(w)=Iz-w|<e},在D叭Be(w上使 用Cauchy-Goursat定理有

Cauchy 积分公式 定理 设 𝐷 为有界区域，其边界 𝜕𝐷 由有限条互不相交的逐段光滑的简 单闭曲线构成，函数 𝑓 在 𝐷 内解析并连续到边界，𝑤 为 𝐷 内一点，则 න 𝜕𝐷 𝑓 𝑧 𝑧 − 𝑤 d𝑧 = 2𝜋𝑖𝑓 𝑤 ， 这里 𝜕𝐷 取正向． 证明 取 𝑤 在 𝐷 内的 𝜀-邻域 𝐵𝜀 𝑤 = { 𝑧 − 𝑤 < 𝜀}，在 𝐷\𝐵𝜀 (𝑤) 上使 用 Cauchy-Goursat 定理有

Cauchy积分公式的证明 f②dz=0, Ja(D八B(w)z-w 于是 f②d 另一方面，利用圆周的参数方程，得 2π 令ε→0，得 )0-m) 2π JaD Z-W

Cauchy 积分公式的证明 න 𝜕(𝐷\𝐵𝜀 𝑤 ) 𝑓 𝑧 𝑧 − 𝑤 d𝑧 = 0， 于是 න 𝜕𝐷 𝑓 𝑧 𝑧 − 𝑤 d𝑧 = න 𝑧−𝑤 =𝜀 𝑓 𝑧 𝑧 − 𝑤 d𝑧 ． 另一方面，利用圆周的参数方程，得 න 𝑧−𝑤 =𝜀 𝑓 𝑧 𝑧 − 𝑤 d𝑧 = න 0 2𝜋 𝑓 𝑤 + 𝜀𝑒 𝑖𝜃 𝜀𝑒 𝑖𝜃 d(𝑤 + 𝜀𝑒 𝑖𝜃 ) = න 0 2𝜋 𝑓 𝑤 + 𝜀𝑒 𝑖𝜃 𝑖d𝜃 ， 令 𝜀 → 0，得 න 𝜕𝐷 𝑓 𝑧 𝑧 − 𝑤 d𝑧 = න 0 2𝜋 𝑓 𝑤 𝑖d𝜃 = 2𝜋𝑖𝑓(𝑤)．

03 PART Cauchy高阶导数公式

Cauchy 高阶导数公式 03 PART

Cauchy高阶导数公式 定理设D为有界区域，其边界∂D由有限条互不相交的逐段光滑的简 单闭曲线构成，函数f在D内解析并连续到边界，w为D内一点，n 为正整数，则 n也=2anfo6w） f() n! 这里aD取正向. 注由高阶导数公式知，解析函数存在任意阶导数！特别，解析函数的导 数也是解析的 推论若复变函数f在区域内存在原函数，则f必在该区域内解析·

Cauchy 高阶导数公式 定理 设 𝐷 为有界区域，其边界 𝜕𝐷 由有限条互不相交的逐段光滑的简 单闭曲线构成，函数 𝑓 在 𝐷 内解析并连续到边界，𝑤 为 𝐷 内一点，𝑛 为正整数，则 න 𝜕𝐷 𝑓 𝑧 𝑧 − 𝑤 𝑛+1 d𝑧 = 2𝜋𝑖 𝑓 𝑛 𝑤 𝑛! ， 这里 𝜕𝐷 取正向． 注 由高阶导数公式知，解析函数存在任意阶导数！特别，解析函数的导 数也是解析的． 推论 若复变函数 𝑓 在区域内存在原函数，则 𝑓 必在该区域内解析．

高阶导数公式的证明 证明在Cauchy积分公式 dz=2πif(w) 两边关于w求n阶导数，得到 2mw=n(2也=na， 将！移至左侧即完成证明

高阶导数公式的证明 证明 在 Cauchy 积分公式 න 𝜕𝐷 𝑓 𝑧 𝑧 − 𝑤 d𝑧 = 2𝜋𝑖𝑓 𝑤 两边关于 𝑤 求 𝑛 阶导数，得到 2𝜋𝑖𝑓 𝑛 𝑤 = න 𝜕𝐷 d 𝑛 d𝑤𝑛 𝑓 𝑧 𝑧 − 𝑤 d𝑧 = න 𝜕𝐷 𝑛! 𝑓 𝑧 𝑧 − 𝑤 𝑛+1 d𝑧 ， 将 𝑛! 移至左侧即完成证明．