同济大学：《数值分析》课程教学资源（讲义）第六章 数值积分 Numerical Quadrature

Numerical Quadrature →Introduction ●Riemann Integration .Composite Trapezoid Rule Composite Simpson's Rule ●Gaussian Quadrature Copyright©2011NA⊙Yin 2

Numerical Quadrature ⇒ Introduction • Riemann Integration • Composite Trapezoid Rule • Composite Simpson’s Rule • Gaussian Quadrature Copyright c 2011 NAYin 2

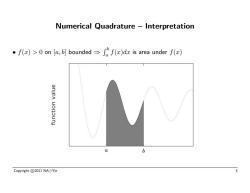
Numerical Quadrature -Interpretation f()>on [a,]boundedf()da is area under f() anjen uonounj b Copyright©2011NA⊙Yin 3

Numerical Quadrature – Interpretation • f(x) > 0 on [a, b] bounded ⇒ R b a f(x)dx is area under f(x) Copyright c 2011 NAYin 3

Motivation Analytical solution-rare rπ/ sin(c)dr=-cosx6/2=-(0-1)=1 ●In general: π/2 (1-a2sin20)1/3d0 o e da Need general numerical technique Copyright 2011 NAOYin 4

Motivation • Analytical solution – rare Z π/2 0 sin(x)dx = − cos x| π/2 0 = −(0 − 1) = 1 • In general: Z π/2 0 (1 − a 2 sin2 θ) 1/3 dθ Z 1 0 e −x 2 dx Need general numerical technique Copyright c 2011 NAYin 4

Definitions ●Mesh:P≡{a=xo<x1<·<xn=b},n subintervals(n+1 points) ●Infima and superma: m=inf{f(c):xa≤x≤x+1} M≡sup{f(x):x≤x≤c+1} Two methods(i.e.,integral estimates):lower and upper sums n1 f,P)=∑m,(1-x) i=0 Copyright©2011NA⊙Yin 5

Definitions • Mesh: P ≡ {a = x0 < x1 < · · · < xn = b}, n subintervals (n + 1 points) • Infima and superma: mi ≡ inf{f(x) : xi ≤ x ≤ xi+1} Mi ≡ sup{f(x) : xi ≤ x ≤ xi+1} • Two methods (i.e., integral estimates): lower and upper sums L(f, P) ≡ n X−1 i=0 mi(xi+1 − xi) Copyright c 2011 NAYin 5

n-1 U(f,P)≡ Mi(xi+1-xi) i=0 ●For example Copyright©2011NA⊙Yin 6

U(f, P) ≡ n X−1 i=0 Mi(xi+1 − xi) • For example Copyright c 2011 NAYin 6

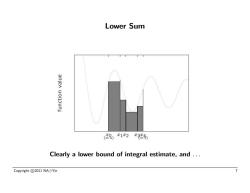
Lower Sum anjen uollunj 9)x1x2r4) Clearly a lower bound of integral estimate,and... Copyright©2011NA⊙Yin 7

Lower Sum Clearly a lower bound of integral estimate, and . . . Copyright c 2011 NAYin 7

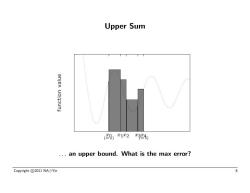
Upper Sum anjen uoloun 9x12r4 ..an upper bound.What is the max error? Copyright©2011NA⊙Yin 8

Upper Sum . . . an upper bound. What is the max error? Copyright c 2011 NAYin 8

Example Third method.use lower and upper sums:(L+U)/2 ●f(x)=x2,[a,b=[0,1andP={0,,2,,1} ·L=品，U=2 ·(L+U)/2=是(actual) .naive approach:still error of ●Max error:(U-L)/2= Is this good enough? Copyright©2011NA⊙Yin

Example • Third method. use lower and upper sums: (L + U)/2 • f(x) = x 2 , [a, b] = [0, 1] and P = {0, 1 4 , 1 2 , 3 4 , 1} • L = 7 32, U = 15 32 • (L + U)/2 = 11 32 (actual 1 3 ) • naive approach: still error of 1 96. • Max error: (U − L)/2 = 1 8 Is this good enough? Copyright c 2011 NAYin 9

Rethinking Perhaps lower and upper sums are enough? error seems small work seems small as well But:estimate of max error was not small ( ·Do they converge to integral as n→o? Will the extrema always be easy to calculate?Accurately?(Probably not!) Proceed in theoretical and practical directions. Copyright©2011NA⊙Yin 10

Rethinking • Perhaps lower and upper sums are enough? ∗ error seems small ∗ work seems small as well • But: estimate of max error was not small (1 8 ) • Do they converge to integral as n → ∞? • Will the extrema always be easy to calculate? Accurately? (Probably not!) Proceed in theoretical and practical directions. Copyright c 2011 NAYin 10

Numerical Quadrature ·Introduction →Riemann Integration Composite Trapezoid Rule Composite Simpson's Rule ●Gaussian Quadrature Copyright©2011NA⊙Yin 11

Numerical Quadrature • Introduction ⇒ Riemann Integration • Composite Trapezoid Rule • Composite Simpson’s Rule • Gaussian Quadrature Copyright c 2011 NAYin 11