同济大学：《概率论与数理统计》课程教学资源（讲稿）Chapter 4 Mathematics

Mathematics Probability and Statistics

Mathematics Probability and Statistics

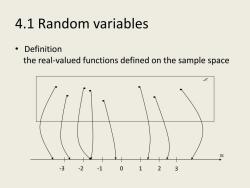
4.1 Random variables 。Definition the real-valued functions defined on the sample space -2 -1 0 3

4.1 Random variables • Definition the real-valued functions defined on the sample space  -3 -2 -1 0 1 2 3 

Random variables can be: Discrete random variables have a countable number of outcomes Examples:Dead/alive,treatment/placebo,dice,counts, etc. Continuous random variables have an infinite continuum of possible values. Examples:blood pressure,weight,the speed of a car,the real numbers from 1 to 6

Random variables can be: • Discrete random variables have a countable number of outcomes – Examples: Dead/alive, treatment/placebo, dice, counts, etc. • Continuous random variables have an infinite continuum of possible values. – Examples: blood pressure, weight, the speed of a car, the real numbers from 1 to 6

Example 1a roll of a die Probability mass function (p.m.f.) X p(x) 1 pX=1=1/6 p(x) 2 PX=2上=1/16 3 pX=31/6 1/6 4 P(X=4)116 1 ll 123456 5 pX=5上1/6 6 pX=6F1/6 ∑P(x)=1 all x

Probability mass function (p.m.f.) x p(x) 1 p(x=1)=1/6 2 p(x=2)=1/6 3 p(x=3)=1/6 4 p(x=4)=1/6 5 p(x=5)=1/6 6 p(x=6)=1/6 x p(x) 1/6 1 2 3 4 5 6 ∑ = all x P(x) 1 Example 1a roll of a die

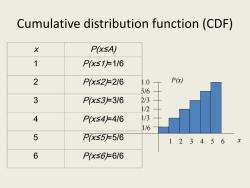
Cumulative distribution function(CDF) X P(xsA) 1 PX≤1F1/6 2 PX≤2F2/6 1.0 P() 5/6 3 PX≤3上=3/6 2/3 1/2 4 P(XS4F416 1/3 6 5 P(xS5516 123456 6 PX≤66/6

Cumulative distribution function (CDF) x P(x) 1/6 1 2 3 4 5 6 1/3 1/2 2/3 5/6 1.0 x P(x≤A) 1 P(x≤1)=1/6 2 P(x≤2)=2/6 3 P(x≤3)=3/6 4 P(x≤4)=4/6 5 P(x≤5)=5/6 6 P(x≤6)=6/6

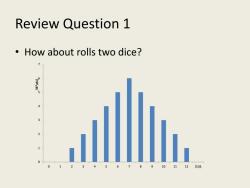
Review Question 1 How about rolls two dice? 12其他

Review Question 1 • How about rolls two dice? 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 8 9 10 11 12 其他 36*p(x)

Review Question 2 Two dice are rolled and the sum of the face values is six.What is the probability that at least one of the dice came up a 3? a. 1/5 b. 2/3 How can you get a 6 on two dice?1- C. 1/2 5,5-1,2-4,4-2,3-3 d 5/6 One of these five has a 3. e. 1.0 .1/5

Review Question 2 Two dice are rolled and the sum of the face values is six. What is the probability that at least one of the dice came up a 3? a. 1/5 b. 2/3 c. 1/2 d. 5/6 e. 1.0 How can you get a 6 on two dice? 1- 5, 5-1, 2-4, 4-2, 3-3 One of these five has a 3. ∴1/5

Example1b(P133) Three balls are to be randomly selected without replacement from an urn containing 20 balls numbered 1 through 20.If we bet that at least one of the drawn balls has a number as large as or larger than 17,what is the probability that we win the bet? ·Solution:0.508

Example1b(P133) • Three balls are to be randomly selected without replacement from an urn containing 20 balls numbered 1 through 20. If we bet that at least one of the drawn balls has a number as large as or larger than 17, what is the probability that we win the bet? • Solution:0.508

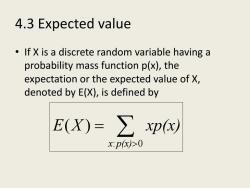
4.3 Expected value If X is a discrete random variable having a probability mass function p(x),the expectation or the expected value of X, denoted by E(X),is defined by E(X)=∑xpy x:p(x)>0

4.3 Expected value • If X is a discrete random variable having a probability mass function p(x), the expectation or the expected value of X, denoted by E(X), is defined by : 0 ( ) x p(x) E X xp(x) > = ∑

Example 3a Find E(X)where X is the outcome when we roll a fair die ·Solution:3.5

Example 3a • Find E(X) where X is the outcome when we roll a fair die • Solution:3.5