同济大学：《概率论与数理统计》课程教学资源（讲稿）Chapter 5 Continuous Random Variables

Chapter 5 Continuous Random Variables

Chapter 5 Continuous Random Variables

5.1 Introduction Examples: (1)The time that a train arrives at a specified stop. (2)The lifetime of a transistor

5.1 Introduction Examples: (1) The time that a train arrives at a specified stop. (2) The lifetime of a transistor

汝Definition We say that X is a continous random variables if there exsists a nonnegative funtions f,defined for all real xE(-,+o),having the property that for any set B of real numbers P({X∈B)=∫f(x) The funtionf is called the probability density funtion of the random var iable X

Definition , ( , ), ({ We say that X is a random variables if there exsists a nonnegative funtions f defined for all real x having the property that for any set B of real num co ber ntinous s P ∈ −∞ +∞ }) ( ) var . B probab X B f x dx The funtion f is called the ility density funt of t io he random i X n able ∈ = ∫

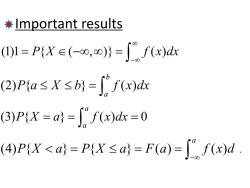
*Important results (1)1=PiXe(0,)=f(x)dx (2)P{a≤X≤b}=∫f(x)d (3)P{X=a}=f(x)d=0 (4)P(X<a=P{Xsa)=F(a)="f(x)d

Important results (1)1 { ( , )} ( ) P X f x dx ∞ −∞ = ∈ −∞ ∞ = ∫ (2) { } ( ) b a P a X b f x dx ≤≤= ∫ (3) { } ( ) 0 a a P X a f x dx = = = ∫ (4) { } { } ( ) ( ) a PX a PX a Fa f xdx −∞ <= ≤= = ∫

Example 1a Suppose that X is a continous random variable whose probability density function is given by f(x)= C(4x-2x2)01)

Example 1a 2 (4 2 ) 0 2 () 0 () ? ( ) ( 1) Suppose that X is a continous random variable whose probability density function is given by Cx x x f x otherwise a what is the value of C b Find P X  −

Example 1b The amount of time,in hours,that a computer functions before breaking down is a continous random var iable with probability density function given by eo0x≥0 f-0 x<0 What is the probabilty that (a)a compupter will funtion between 50 and 150 hours before breaking down; (b)it will funtion less than 100 hours?

Example 1b - /100 , , var 0 () 0 x The amount of time in hours that a computer functions before breaking down is a continous random iable with probability density function given by e x f x λ ≥ = 0 ( ) 50 150 ; ( ) 100 ? x What is the probabilty that a a compupter will funtion between and hours before breaking down b it will funtion less than hours    <

Expectation and variance of continuous random variables If X is a continuous random variable having probability density function f(x),then as f(x)dk≈P{x≤X≤x+dx}for dx smal Define the expected value of X by E(X)=xf(x)dx

Expectation and variance of continuous random variables ( ), ( ) { } If X is a continuous random variable having probability density function f x then as f x dx P x X x dx for dx smal ≈ ≤ ≤+ ( ) () . Define the expected value of X by E X xf x dx ∞ −∞ = ∫

Example 2a Find E(X)when the density function of X is m-“8

Example 2a ( ) 2 0 1 () 0 Find E X when the density function of X is x if x f x otherwise  ≤ ≤ =  

Example 2b The density function of X is given by - f0≤x≤1 otherwise Find E(e)

Example 2b 1 0 1 () 0 ( ). x The density function of X is given by if x f x otherwise Find E e  ≤ ≤ =  

Proposition 2.1 If X is a continuous random variable with probability density function f(x),then for any real-valued funtion g, ELg(x】=g(x)f(x)dx

Proposition 2.1 ( ), - , [ ( )] ( ) ( ) If X is a continuous random variable with probability density function f x then for any real valued funtion g Egx gx f xdx ∞ −∞ = ∫