同济大学：《常微分方程》课程教学资源（讲义）高阶线性微分方程

2.Linear Differential Equations of Higher Order 4口卡0y4主，元，2只0

2. Linear Differential Equations of Higher Order Second-Order Linear Equations Recall a general second-order differential equation G(x, y, y 0 , y 00 ) = 0 It is linear provided that G is linear in the dependent variable y and y 0 , y 00 . A(x)y 00 +B(x)y 0 +C(x)y = F(x) Example e x y 00 + (cos x)y 0 + (1+x)y = tan −1 x y 00 = yy 0 y 00 +3(y 0 ) 2 +4y 3 = 0

2.Linear Differential Equations of Higher Order Second-Order Linear Equations Recall a general second-order differential equation G(x,y,y,y")=0 It is linear provided that G is linear in the dependent variable y and y,y". A(x)y"+B(x)y+C(x)y=F(x) Example e'y"+(cosx)y/+(1+x)y=tan-Ix y"=yy y"+36y)2+4y3=0

2. Linear Differential Equations of Higher Order Second-Order Linear Equations Recall a general second-order differential equation G(x, y, y 0 , y 00) = 0 It is linear provided that G is linear in the dependent variable y and y 0 , y 00 . A(x)y 00 +B(x)y 0 +C(x)y = F(x) Example e x y 00 + (cos x)y 0 + (1+x)y = tan−1 x y 00 = yy 0 y 00 +3(y 0 ) 2 +4y 3 = 0

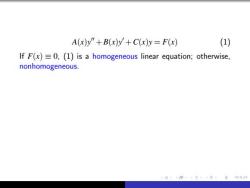
A(x)y"+B(x)y+C(x)y=F(x) (1) If F(x)=0,(1)is a homogeneous linear equation;otherwise, nonhomogeneous. 4日1①y至，无2000

A(x)y 00 +B(x)y 0 +C(x)y = F(x) (1) If F(x) ≡ 0, (1) is a homogeneous linear equation; otherwise, nonhomogeneous. Example x 2 y 00 +2xy 0 +3y−cos x = 0 (nonhomogenous) x 2 y 00 +2xy 0 +3y = 0 (homogeneous)

A(x)y"+B(x)y+C(x)y=F(x) (1) If F(x)=0,(1)is a homogeneous linear equation;otherwise, nonhomogeneous. Example x2y"+2xy+3y-cosx =0 4日10y至，无2000

A(x)y 00 +B(x)y 0 +C(x)y = F(x) (1) If F(x) ≡ 0, (1) is a homogeneous linear equation; otherwise, nonhomogeneous. Example x 2 y 00 +2xy 0 +3y−cos x = 0 (nonhomogenous) x 2 y 00 +2xy 0 +3y = 0 (homogeneous)

A(x)y"+B(x)y+C(x)y=F(x) (1) If F(x)=0,(1)is a homogeneous linear equation;otherwise, nonhomogeneous. Example x2y"+2xy +3y-cosx =0 (nonhomogenous) 4日10y至，无2000

A(x)y 00 +B(x)y 0 +C(x)y = F(x) (1) If F(x) ≡ 0, (1) is a homogeneous linear equation; otherwise, nonhomogeneous. Example x 2 y 00 +2xy 0 +3y−cos x = 0 (nonhomogenous) x 2 y 00 +2xy 0 +3y = 0 (homogeneous)

A(x)y"+B(x)y+C(x)y=F(x) (1) If F(x)=0,(1)is a homogeneous linear equation;otherwise, nonhomogeneous. Example x2y"+2xy+3y-cosx=0 (nonhomogenous) x2y"+2y+3y=0 4日10y至，无2000

A(x)y 00 +B(x)y 0 +C(x)y = F(x) (1) If F(x) ≡ 0, (1) is a homogeneous linear equation; otherwise, nonhomogeneous. Example x 2 y 00 +2xy 0 +3y−cos x = 0 (nonhomogenous) x 2 y 00 +2xy 0 +3y = 0 (homogeneous)

A(x)y"+B(x)y+C(x)y=F(x) (1) If F(x)=0,(1)is a homogeneous linear equation;otherwise, nonhomogeneous. Example x2y"+2xy+3y-cosx=0 (nonhomogenous) x2y"+2xy+3y=0 (homogeneous) 4日10y至，无2000

A(x)y 00 +B(x)y 0 +C(x)y = F(x) (1) If F(x) ≡ 0, (1) is a homogeneous linear equation; otherwise, nonhomogeneous. Example x 2 y 00 +2xy 0 +3y−cos x = 0 (nonhomogenous) x 2 y 00 +2xy 0 +3y = 0 (homogeneous)

A Typical Application In case the differential equation models a physical system, the nonhomogenous term F(x)frequently corresponds to some external influence on the system. 4口1日，1元2000

A Typical Application In case the differential equation models a physical system, the nonhomogenous term F(x) frequently corresponds to some external influence on the system. Suppose that a mass m is attached both to a spring that exerts on it a force FS and to a dashpot (shock absorber) that exerts a force FR on the mass. Assume that the restoring force FS of the spring is proportional to the displacement x (positive to the right, negative to the left) of the mass from equilibrium, and that the dashpot force FR is proportional to the velocity v = dx/dt of the mass. Then we have FS = −kx and FR = −cv (k, c > 0)

A Typical Application In case the differential equation models a physical system, the nonhomogenous term F(x)frequently corresponds to some external influence on the system. Suppose that a mass m is attached both to a spring that exerts on it a force Fs and to a dashpot(shock absorber)that exerts a force FR on the mass. 1口1日，元卡20只0

A Typical Application In case the differential equation models a physical system, the nonhomogenous term F(x) frequently corresponds to some external influence on the system. Suppose that a mass m is attached both to a spring that exerts on it a force FS and to a dashpot (shock absorber) that exerts a force FR on the mass. Assume that the restoring force FS of the spring is proportional to the displacement x (positive to the right, negative to the left) of the mass from equilibrium, and that the dashpot force FR is proportional to the velocity v = dx/dt of the mass. Then we have FS = −kx and FR = −cv (k, c > 0)

A Typical Application In case the differential equation models a physical system, the nonhomogenous term F(x)frequently corresponds to some external influence on the system. Suppose that a mass m is attached both to a spring that exerts on it a force Fs and to a dashpot (shock absorber)that exerts a force FR on the mass.Assume that the restoring force Fs of the spring is proportional to the displacement x(positive to the right,negative to the left)of the mass from equilibrium, 4口①，t元2月00

A Typical Application In case the differential equation models a physical system, the nonhomogenous term F(x) frequently corresponds to some external influence on the system. Suppose that a mass m is attached both to a spring that exerts on it a force FS and to a dashpot (shock absorber) that exerts a force FR on the mass. Assume that the restoring force FS of the spring is proportional to the displacement x (positive to the right, negative to the left) of the mass from equilibrium, and that the dashpot force FR is proportional to the velocity v = dx/dt of the mass. Then we have FS = −kx and FR = −cv (k, c > 0)