华南农业大学：《工程力学》课程教学资源（课件讲稿）第8章 弯曲内力 8.2 剪力和弯矩

问题的引出 梁为什么做成变截面的？ 树枝会在哪儿断呢？

问题的引出 梁为什么做成变截面的？ 树枝会在哪儿断呢？

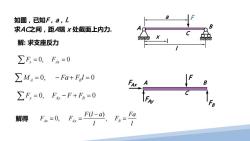
如图，已知F,a,人 求AC之间，距A端X处截面上内力. 解：求支座反力 ∑F=0,Fx=0 ∑MA=0,-Fa+Fl=0 FAx A ∑E,=0,F-F+FB=0 解得 Fs=0,5,F0-a Fa ,F1

如图，已知F，a，l. 求AC之间，距A端 x 处截面上内力. 解: 求支座反力 FAy FAx F B A B F C 0, 0 ∑F F x = = Ax ( ) 0, , Ax Ay B F l a Fa FF F l l − 解得 = = = 0, 0 ∑ M Fa F l A B = −+ = 0, 0 ∑F F FF y = −+ = Ay B A B a l F C x

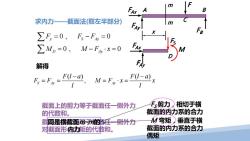
m FAx A 求内力 截面法（取左半部分） ∑F=0，F、-Fw=0 ∑MD=0,M-Fx=0 解得 F(-a).M=Fw3-F(-ax 截面上的剪力等于截面任一侧外力 E剪力)相切于横 的代数和。 截面的内力系的合力 截同是横截面筋的年任一侧外力 M弯矩，垂直于横 对截面形内力矩的代数和。 截面的内力系的合力 偶矩

截面上的弯矩等于截面任一侧外力 对截面形心力矩的代数和。 FS 剪力，相切于横 截面的内力系的合力 M 弯矩，垂直于横 截面的内力系的合力 偶矩 同是横截面m-m的 内力 截面上的剪力等于截面任一侧外力 的代数和。 FAy FAx F B A B m F m x 求内力——截面法 C (取左半部分) 0 , 0 0 , 0 y S Ay D Ay F FF M MF x = −= = − ⋅= ∑ ∑ M FAy F S D FAx 解得 ( ) ( ) , S Ay Ay Fl a Fl a F F MFx x l l − − = = = ⋅=

以右两部分为研究对象也可求出F A 和M,且数值相等但方向相反。 (正负的规定)》 剪力对梁上任意一点的矩为顺 时针转向时，剪力为正；反之 + Fs 为负。 左上右下为正； 反之为负 截面上的弯矩使得梁呈凹形 月M 为正；反之为负。 左顺右逆为正； 反之为负

剪力对梁上任意一点的矩为顺 时针转向时，剪力为正；反之 为负。 截面上的弯矩使得梁呈凹形 为正；反之为负。 左上右下为正； 反之为负 左顺右逆为正； 反之为负 以右两部分为研究对象也可求出Fs 和M，且数值相等但方向相反。 （正负的规定） + _ FS FS FS FS + M M M M _ F F B F S D M M FAy F S D FAx

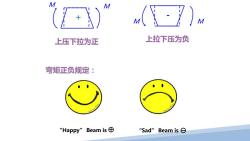
M 上压下拉为正 上拉下压为负 弯矩正负规定： “Happy"Beam is⊕ “Sad"Beam is

上压下拉为正 + M M 上拉下压为负 - M M 弯矩正负规定： “Happy” Beam is ⊕ “Sad” Beam is 

例1.求图示简支梁E截面的内力 求E截面的内力 解：1.确定支反力 Me=Fa ∑M=0 -F3a+2F.2a+F.a=0 1.5aC D ∑M4=0 F·3a+Fa-2F·a=0 2.用截面法研究内力 5F F 3 3 ∑F,=0 2F+FSE=FAy FSE=- F 3 ∑。-02F号+M:=E 3a ME= Fa 2

FAy 解：1. 确定支反力 FAy F By 0 ∑ MB = 3 22 0 − ⋅ + ⋅ + ⋅= F a F a Fa Ay ∑ M A = 0 3 20 F a Fa F a By ⋅ + − ⋅= 3 By F F = 5 3 Ay F 2. 用截面法研究内力 F = FSE ME ∑Fy = 0 2FF F + = SE Ay 0 ∑ MO = 3 2 2 2 E Ay a a F MF ⋅+ = ⋅ 例1.求图示简支梁 E 截面的内力 O

Me=Fa 若分析右段，得到： SE ∑F,=0FE+F,=0 F Fse=-Foy=-3 ∑M。=0 Mg=FRy'2 ME= 3Fa 2

F By FSE ME O 若分析右段，得到： ∑Fy = 0 FSE + FBy = 0 0 ∑ MO = Fa a ME = FBy ⋅ + 2 3

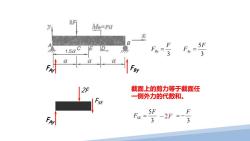
2F Me=Fa F 5F 1.5aC 3 3 By 截面上的剪力等于截面任 一侧外力的代数和。 5F FSE= 3 -2F=- 3

FAy F By 3F FBy = 35F FAy = 截面上的剪力等于截面任 一侧外力的代数和。 35F FSE = FAy FSE 2F 3F = −

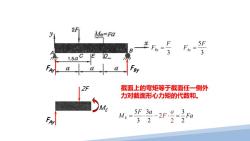
2F Me=Fa F时 F 5F 3 3 1.5aC a 2F 截面上的弯矩等于截面任一侧外 力对截面形心力矩的代数和。 5F 3a Mg= -2F.0=3 Fa 32 22

FAy F By 3 F FBy = 3 5F FAy = 截面上的弯矩等于截面任一侧外 力对截面形心力矩的代数和。 2 3 3 5F a ME = ⋅ Fa 2 3 = ME FAy 2F

例2.外伸梁受集中力F和集中力偶M=Fa作用，如图所示。 求：截面1、2、3、4上的剪力和弯矩。 M=Fa 截面1：无限接近C点，在C左侧 1山2 截面2：无限接近C点，在C右侧 截面3：无限接近B点，在B左侧 截面4：无限接近B点，在B右侧 FA 解：①先确定约束力 ∑M4=0-M+fF22a-F-3a=0 ∑F,=0 F+FR-F=0 解得F4=-F F=2F

例 2. 外伸梁受集中力 F 和集中力偶 M=Fa 作用，如图所示。 a F B A a a 1 2 3 4 C M=Fa 求：截面1、2、3、4上的剪力和弯矩。 解：①先确定约束力 0 2 3 0 M M F aFa A B ∑ = − + ⋅ −⋅ = 0 0 ∑F FFF y AB = + −= F A F B 解得 2 FF FF A B =− = 截面1：无限接近C点，在C左侧 截面2：无限接近C点，在C右侧 截面3：无限接近B点，在B左侧 截面4：无限接近B点，在B右侧