华南农业大学：《工程力学》课程教学资源（课件讲稿）第9章 弯曲应力 9.2 弯曲正应力的强度条件及其应用

9.2弯曲正应力的强度条件及其应用 1、变形几何关系 综合考虑 2、物理关系 3、静力学关系

综合考虑 1、变形几何关系 2、物理关系 3、静力学关系 9.2 弯曲正应力的强度条件及其应用

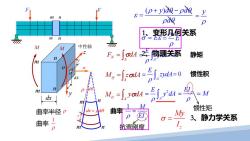
(p+y)a服-pd m 、y n p昶 p m n 合形见回关系 M M 中性轴 静矩 n R=小12片胸理关系 m 0 dA M,=jFom=」，34=0 惯性积 m =M dx 曲率半径P 曲率 惯性矩 y 曲率 3、静力学关系 p 抗弯刚度

dx m m n n o z y ρ dθ m m n n F F y ( ) yd d d ρ θ ρθ ε ρ θ + − = y ρ = σ ε = E y E ρ = M M 中性轴 y z dA σ ∫A FN = σdA ∫A Miy = zσdA ∫A Miz = yσdA A E ydA ρ = ∫ = 0 A E zydA ρ = ∫ = 0 2 A E y dA ρ = ∫ EI z ρ = 1 z M ρ EI = 1、变形几何关系 2、物理关系 = M 3、静力学关系 惯性矩 抗弯刚度 曲率半径 ρ 曲率 1 ρ 静矩 惯性积 曲率 m n m n dx d = ρ θ z My I σ =

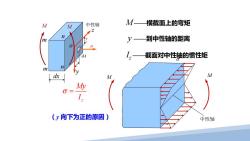
M M 中性轴 M一横截面上的弯矩 n y 到中性轴的距离 截面对中性轴的惯性矩 m n dx M M My (y向下为正的原因) 中性轴

M ——横截面上的弯矩 y ——到中性轴的距离 Iz ——截面对中性轴的惯性矩 M σ 中性轴 M （y 向下为正的原因） dx m m n n o z y M M 中性轴 y z dA σ z My I σ =

Tianiin yai P a a a anmn Inversity Mvecha e5ya©a0Cs Tianiin Univers海w Tan通 aniin University Mechanics Fianiin Univers lecnanics wGa0图 Tianiin Universiy aity Me

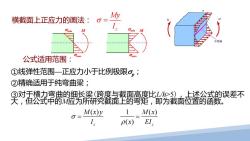
My 横截面上正应力的画法：σ= Omin M 性 公式适用范围： ①线弹性范围一正应力小于比例极限σ，； ②精确适用于纯弯曲梁； ③对于横力弯曲的细长梁（跨度与截面高度比L>5),上述公式的误差不 天，但公式中的应为所研究截面上的弯矩，即为截面位置的函数。 M(x)y 1 M(x) O= (x) EI

横截面上正应力的画法： σmin M σmax σmin M σmax ①线弹性范围—正应力小于比例极限σp； ②精确适用于纯弯曲梁； ③对于横力弯曲的细长梁(跨度与截面高度比L/h>5)，上述公式的误差不 大，但公式中的M应为所研究截面上的弯矩，即为截面位置的函数。 公式适用范围： () 1 () ( ) z z Mxy M x I x EI σ ρ = = M σ 中性轴 M z My I σ =

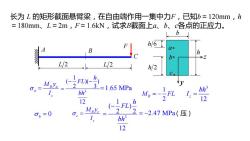
长为L的矩形截面悬臂梁，在自由端作用一集中力F,已知b=120mm,h =180mm、L=2m,F=1.6kN,试求B截面上a、b、c各点的正应力。 6 h/61 B bo L/2 L/2 h/2 0a= FL3=165 MPa bh LFL bh MB 1.= 12 12 h (-FL) 06=0 2=-2.47MPa(压) bh3 12

长为 L 的矩形截面悬臂梁，在自由端作用一集中力F，已知b＝120mm，h ＝180mm、L＝2m，F＝1.6kN，试求B截面上a、b、c各点的正应力。 L 2 F L 2 A B C 1 2 M FL B = − 3 12 z bh I = B a a z M y I σ = 3 1 ( )( ) 2 3 12 h FL bh − − = =1.65 MPa 0 σ b = B c c z M y I σ = 3 1 ( ) 2 2 12 h FL bh − = = −2.47 MPa（压） b h h 6 h 2 a b c z y

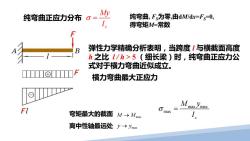
纯弯曲正应力分布σ= My 纯弯曲，F为零，由dMWd=F=0, 得弯矩M-常数 B 弹性力学精确分析表明，当跨度1与横截面高度 h之比I/h>5(细长梁)时，纯弯曲正应力公 式对于横力弯曲近似成立。 横力弯曲最大正应力 弯矩最大的截面M→Mma 离中性轴最远处y→ymax

纯弯曲正应力分布 弹性力学精确分析表明，当跨度 l 与横截面高度 h 之比 l / h > 5 （细长梁）时，纯弯曲正应力公 式对于横力弯曲近似成立。 max max max z M y I σ = 横力弯曲最大正应力 弯矩最大的截面 M M → max 离中性轴最远处 max y y → 纯弯曲, FS为零,由dM/dx=FS=0, z 得弯矩M=常数 My I σ =

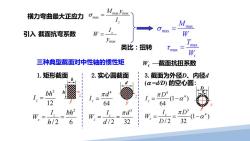
横力弯曲最大正应力 Mmax ymas max 引入截面抗弯系数 W W 类比：扭转 max W 三种典型截面对中性轴的惯性矩 W,一截面抗扭系数 1.矩形截面 2.实心圆截面 3.截面为外径D、内径d (a=d/D)的空心圆： 1= bh 12 / πd 1=D 1-a) 64 4 W bh2 < TD3 h/2 6 W.= d/2 32 W D/2 32(1-a)

1.矩形截面 三种典型截面对中性轴的惯性矩 2.实心圆截面 3.截面为外径D、内径d (α =d/D) 的空心圆: 截面抗弯系数 max max max z M y I 横力弯曲最大正应力 σ = max z I W y = max max M W σ = 3 2 12 /2 6 z z z bh I I bh W h = = = 4 3 64 / 2 32 z z z d I I d W d π π = = = 4 4 3 4 (1 ) 64 (1 ) / 2 32 z z z D I I D W D π α π α = − = = − Wt —截面抗扭系数 max max t T W 类比：扭转 τ = z d y b h z y z D d y 引入

弯曲正应力的强度条件 Mmasymaxa] 或 M<[o] 1.弯矩最大的截面上 2.离中性轴最远处 3.非常规截面或变截面梁要综合考虑M与I: 4.脆性材料抗拉和抗压性能不同，二方面都要考虑 Omax≤[o,] oc,max≤[oe]

弯曲正应力的强度条件 [ ] max max max z M y I σ σ = ≤ 1.弯矩最大的截面上 2.离中性轴最远处 4.脆性材料抗拉和抗压性能不同，二方面都要考虑 [ ] σ t,max ≤ σ t [ ] σ c,max ≤ σ c 3.非常规截面或变截面梁要综合考虑 M 与 Iz [ ] max max M W 或 σ σ = ≤

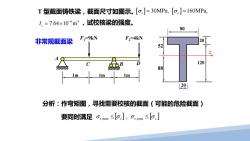
T型截面铸铁梁，截面尺寸如图示。[o,]=30MPa,[o。]=160MPa, 1.=7.64×106m4,试校核梁的强度。 80 非常规截面梁 F=9kN F2=4kN 52 120 88 1m 20 分析：作弯矩图，寻找需要校核的截面（可能的危险截面） 要同时满足oms≤[o,小，o。nmx≤[o]

分析：作弯矩图，寻找需要校核的截面（可能的危险截面） [ ] [ ] σ t,max ≤ σ t σ c,max ≤ σ c 要同时满足 , 非常规截面梁 F1=9kN F2=4kN A C B D 1m 1m 1m T 型截面铸铁梁，截面尺寸如图示。 ，试校核梁的强度。 [σ σ t c ] = 30MPa, 160MPa, [ ] = 6 4 I z 7.64 10 m− = × 80 52 88 20 20 120 z