西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2015)23 广义特征值与极小极大原理

矩阵论 主讲教师:徐乐 2015年1月13日星期二
2015年1月13日星期二 矩 阵 论 主讲教师:徐乐

上讲回顾 ÷第22讲矩阵特征值估计 ·特征值界的估计 ·盖尔圆法 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 2 上讲回顾 第22讲 矩阵特征值估计 特征值界的估计 盖尔圆法

特征值界的估计 冬矩阵特征值估计 ·特征值计算较困难,希望找到简便的特征值界 限或分布范围的估计方法 冬定理1 ·设A∈R×n,为A的任意特征值,则有 m()sx-D ·其中 M=max ai-ai 1Si,jSn 2 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 3 特征值界的估计 矩阵特征值估计 特征值计算较困难,希望找到简便的特征值界 限或分布范围的估计方法 定理1 设A∈Rn×n,λ为A的任意特征值,则有 • 其中 nn 1 Im M 2 ij ji 1 i,j n a a M max 2
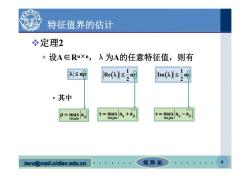
特征值界的估计 冬定理2 ·设A∈Rn×n,入为A的任意特征值,则有 ≤吗 Re()s Im(Z)s ·其中 p=maxa可 t=max ai +a s=max ai-aj 1si,jSn 1Si,jSn l 1si,iSn I lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 4 特征值界的估计 定理2 设A∈Rn×n,λ为A的任意特征值,则有 • 其中 n 1 Re n2 1 Im ns 2 ij 1 i,j n max a ij ji 1 i,j n max a a ij ji 1 i,j n s max a a

盖尔圆法 必定义 ·设A=(anXn∈RnXn, 由方程所确定的圆称为A 的第个盖尔圆,R称为盖尔圆的半径 -R,=aol izi 定理3 ·矩阵A的所有特征值均落在它的所有盖尔圆的 并集之中 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 5 盖尔圆法 定义 设A=(ai,j)n×n∈Rn×n,由方程所确定的圆称为A 的第i个盖尔圆,Ri称为盖尔圆的半径 定理3 矩阵A的所有特征值均落在它的所有盖尔圆的 并集之中 n ii i ij j 1 i j za R a

盖尔圆法 冬定理4 ·将矩阵A的全体盖尔圆的并集按连通部分分成 若干个子集 ·一个子集由完全连通的盖尔圆组成,不同子集没有 相连通的部分 ·对每个子集,若它恰好由K个盖尔圆组成,则该子 集中恰好包含A的K个特征值 ·说明 ·盖尔圆相互重叠时重复计算,特征值相重时也重复 计算 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 6 盖尔圆法 定理4 将矩阵A的全体盖尔圆的并集按连通部分分成 若干个子集 • 一个子集由完全连通的盖尔圆组成,不同子集没有 相连通的部分 • 对每个子集,若它恰好由K个盖尔圆组成,则该子 集中恰好包含A的K个特征值 说明 • 盖尔圆相互重叠时重复计算,特征值相重时也重复 计算

盖尔圆法 冬推论 ·孤立盖尔圆中恰好包含一个特征值 实矩阵的孤立盖尔圆恰好包含一个实特征值 ·盖尔圆方法中盖尔圆半径可以按列求和(因为方 阵转置后特征值不变) ·盖尔圆半径变为R,两个盖尔圆定理仍然成立 a i=1 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 7 盖尔圆法 推论 孤立盖尔圆中恰好包含一个特征值 实矩阵的孤立盖尔圆恰好包含一个实特征值 盖尔圆方法中盖尔圆半径可以按列求和(因为方 阵转置后特征值不变) 盖尔圆半径变为Ri,两个盖尔圆定理仍然成立 n ' i i ij j 1 j R a

盖尔圆法 说明 ·相似矩阵P1AP与A具有相同的特征值,取 P=diag[a az.a(a>0) 1 0 01 0 1 B=PAP= &2 02 0 0 lexu@mail.xidian.edu.cn 矩阵论→
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 8 盖尔圆法 说明 相似矩阵P-1AP与A具有相同的特征值,取 P diag , 0 12 n i 1 1 1 2 2 ij n n 1 0 0 1 B P AP a 0 1 0 i ij j a

第23讲广义特征值与极小极大原理 冬广义特征值问题 瑞利商 冬极小极大原理 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 9 第23讲 广义特征值与极小极大原理 广义特征值问题 瑞利商 极小极大原理

广义特征值问题 冬定义 ·设A、B为n阶方阵,若存在数入,使得方程 Ax=λBx存在非零解 ·则称入为A相对于B的广义特征值 ·x为A相对于B的属于广义特征值入的特征向量 一是标准特征值问题的推广 ©当B=I(单位矩阵)时,广义特征值问题退化为标准 特征值问题。 一特征向量是非零的 lexu@mail.xidian.edu.cn 矩阵论 10
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 10 广义特征值问题 定义 设A、B为n阶方阵,若存在数λ,使得方程 Ax=λBx存在非零解 • 则称λ为A相对于B的广义特征值 • x为A相对于B的属于广义特征值λ的特征向量 – 是标准特征值问题的推广 当B=I(单位矩阵)时,广义特征值问题退化为标准 特征值问题。 – 特征向量是非零的
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2015)22 范数理论及特征值估计.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2015)21 范数理论.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)20 全面最小二乘法.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)19 最小二乘法.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)18 广义逆的应用.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)17 Penrose广义逆与Moore广义逆.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)16 Penrose广义逆与Moore广义逆.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)15 Penrose广义逆的性质.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)14 矩阵的奇异值分解.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)13 QR分解及满秩分解.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)12 矩阵的QR分解.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2011)11 Penrose广义逆矩阵的定义及存在性.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)10 矩阵三角分解.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)09 矩阵函数及其微积分.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)08 矩阵函数的求解.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)07 Jordan标准形分析.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)06 Jordan标准形.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)05 矩阵对角化.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)04 线性变换矩阵及其对角化.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)03 直和及线性变换.pdf
- 同济大学:工程硕士研究生教材《数值分析与矩阵论》书籍PDF电子版(工程数学,上册).pdf
- 高等学校研究生教材:《有限单元法》书籍PDF电子版 Finite Element Method(共十七章,编著:薛守义).pdf
- 高等学校教材:《近世代数》书籍PDF电子版(第二版,编著:杨子胥,共六章).pdf
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.1 消元法.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.2 n维向量空间.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.3 线性相关性.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.4 矩阵的秩.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.5 线性方程组有解判别定理.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.6 线性方程组解的结构.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第四章 矩阵 4.1 矩阵的概念.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第四章 矩阵 4.2 矩阵的运算.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第四章 矩阵 4.3 矩阵乘积的行列式与秩.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第四章 矩阵 4.4 矩阵的逆.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第四章 矩阵 4.5 矩阵的分块.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第四章 矩阵 4.6 初等矩阵.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第四章 矩阵 4.7 分块乘法的初等变换及应用.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第五章 二次型 5.1 二次型的矩阵表示.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第六章 线性空间 6.1 集合与映射.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第六章 线性空间 6.2 线性空间的定义与简单性质.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第六章 线性空间 6.3 维数,基与坐标.pptx
