西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第四章 矩阵 4.5 矩阵的分块

西安毛子科技大学XIDIAN UNIVERSITY$4.5矩阵的分块、分块矩阵的概念二、分块矩阵的运算三、准对角矩阵
一、分块矩阵的概念 二、分块矩阵的运算 三、准对角矩阵

西安毛子科技大学一XIDIAN UNIVERSITY一、分块矩阵的概念定义 设A是一个矩阵,在A的行或列之间加上一些线,把这个矩阵分成若干小块.用这种方法被分成若于小块的矩阵叫做一个分块矩阵每一个分块的方法叫做A一种分法
一、分块矩阵的概念 定义 设A是一个矩阵,在A的行或列之间加上 一些线,把这个矩阵分成若干小块.用这种 方法被分成若干小块的矩阵叫做一个分块矩阵. 每一个分块的方法叫做A一种分法.

西安毛子科技大学XIDIAN UNIVERSITY特殊分法设矩阵 A=(aj)sn"(A)A按行分块 A=其中 A, =(ai1,ai2,"",ain),:i =1,2,...,s.A.aiani按列分块A=(A,A,,A),其中A,=...j=1,2,...,nari)
特殊分法 按行分块 1 2 , s A A A A = 其中 1 2 ( , , , ), A a a a i i i in = 按列分块 A A A A = ( 1 2 , , , n ) ,其中 1 2 , j j j nj a a A a = 设矩阵 ( ) , A a = ij s n j n = 1,2, , . i s = 1,2, ,

西安毛子科技大学二XIDIAN UNIVERSITY一、分块矩阵的运算1、加法设A,B是两个 m×n矩阵,对它们用同样的分法分块:B.B.A11A=B.BBA其中子块 A,与 B,为同型矩阵,则A1+ BA+B=+BsIB
= = s sr r s sr r B B B B B A A A A A 1 1 1 1 1 1 1 1 , 1、加法 设 A, B 是两个 m n 矩阵,对它们 一、分块矩阵的运算 . 1 1 1 1 1 1 1 1 + + + + + = s s sr sr r r A B A B A B A B A B 用同样的分法分块: 其中子块 Aij 与 Bij 为同型矩阵,则

西安毛子科技大学XIDIAN UNIVERSITY2、数量乘法aeP,则设分块矩阵A=A.1A.(2Au2A2A=2A.12As
2、数量乘法 . 1 1 1 1 = s srr A A A A A 设分块矩阵 11 1 1 , , r s sr A A A P A A = 则

西要毛子科技大学-XIDIANUNIVERSITY3、乘法把矩阵 A=(aik)mn,B=(bj)nxp分块成B11AlAtBurA=B=Bt1...BrAs1A.其中Ai,A2,A,的列数分别等于Bu,B2,,B的行数,那么(CuCirAB=::CC.其中C,=A,B(i=-l,...,s; j-l,,r)k=l
, , 1 1 1 1 1 1 1 1 = = t tr r s st t B B B B B A A A A A 1 2 1 2 , , , , , , , 其中A A A B B B i i it j j ij 的列数分别等于 的行数 那么 = s sr r C C C C AB 1 11 1 ( 1, , ; 1, , ). 1 C A B i s j r k j t k i j = i k = = = 其 中 3、乘法 把矩阵 ( ) , ( ) A a B b = = ik m n kj n p 分块成
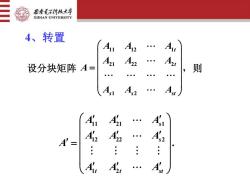
西安毛子科技大学XIDIANUNIVERSIT4、转置A.A12mA223则设分块矩阵 A=AsA.A.SstA'Al1A21s1A2A2A's2:::A'AfA
11 21 1 12 22 2 1 2 . ss t t st A A A A A A A A A A = 设分块矩阵 11 12 1 21 22 2 1 2 , tt s s st A A A A A A A A A A = 则 4、转置

西安毛子科技大学XIDIAN UNIVERSITY设例1 0001001100070-121A=B =2010141111201-1求 AB
例1 设 , 1 1 0 1 1 2 1 0 0 1 0 0 1 0 0 0 − A = , 1 1 2 0 1 0 4 1 1 2 0 1 1 0 1 0 − − − B = 求 AB
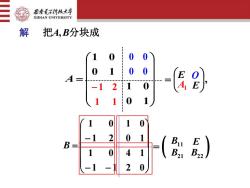
西安毛子律技大枣XIDIANUNIVERSITY解把A,B分块成00102110002BuEB :0B21B224110-12
解 把A,B分块成 = 0 1 1 0 0 1 1 0 A 0 0 0 0 1 1 − 1 2 , = E E O A1 − − − = 1 1 2 0 1 0 4 1 1 2 0 1 1 0 1 0 B ( ) = B11 E B21 B22

西安毛子律技大学XIDIANUNIVERSITYE0EBu1则AB :B22 E儿B21AlEBr1A +B,B + B210又 A,Bu + B210S
则 = 21 22 11 1 B B B E A E E O AB . 1 11 21 1 22 11 + + = A B B A B B E 又 A1 B11 + B21 − − + − − = 1 1 1 0 1 2 1 0 1 1 1 2 − − + − = 1 1 1 0 0 2 3 4 , 1 1 2 4 −− = + − + = 2 0 4 1 1 1 1 2 A1 B22 , 3 1 3 3 =
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第四章 矩阵 4.4 矩阵的逆.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第四章 矩阵 4.3 矩阵乘积的行列式与秩.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第四章 矩阵 4.2 矩阵的运算.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第四章 矩阵 4.1 矩阵的概念.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.6 线性方程组解的结构.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.5 线性方程组有解判别定理.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.4 矩阵的秩.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.3 线性相关性.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.2 n维向量空间.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.1 消元法.pptx
- 高等学校教材:《近世代数》书籍PDF电子版(第二版,编著:杨子胥,共六章).pdf
- 高等学校研究生教材:《有限单元法》书籍PDF电子版 Finite Element Method(共十七章,编著:薛守义).pdf
- 同济大学:工程硕士研究生教材《数值分析与矩阵论》书籍PDF电子版(工程数学,上册).pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2015)23 广义特征值与极小极大原理.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2015)22 范数理论及特征值估计.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2015)21 范数理论.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)20 全面最小二乘法.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)19 最小二乘法.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)18 广义逆的应用.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)17 Penrose广义逆与Moore广义逆.pdf
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第四章 矩阵 4.6 初等矩阵.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第四章 矩阵 4.7 分块乘法的初等变换及应用.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第五章 二次型 5.1 二次型的矩阵表示.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第六章 线性空间 6.1 集合与映射.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第六章 线性空间 6.2 线性空间的定义与简单性质.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第六章 线性空间 6.3 维数,基与坐标.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第六章 线性空间 6.5 线性子空间.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第六章 线性空间 6.6 子空间的交与和.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第六章 线性空间 6.7 子空间的直和.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第六章 线性空间 6.8 线性空间的同构.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第七章 线性变换 7.1 线性变换的定义.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第七章 线性变换 7.2 线性变换的运算.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第七章 线性变换 7.3 线性变换的矩阵.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第七章 线性变换 7.4 特征值与特征向量.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第七章 线性变换 7.5 对角矩阵.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第七章 线性变换 7.6 线性变换的值域与核.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第七章 线性变换 7.7 不变子空间.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第七章 线性变换 7.8 若尔当标准形介绍.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第七章 线性变换 7.9 最小多项式.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第八章 λ-矩阵 8.1 λ-矩阵.pptx
