西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)15 Penrose广义逆的性质

矩阵论 主讲教师:徐乐 2014年12月10日星期三
2014年12月10日星期三 矩 阵 论 主讲教师:徐乐

上讲回顾 第14讲矩阵的奇异值分解 ·酉对角分解 ·一般矩阵的奇异值分解 ·Penrose)广义逆 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 2 上讲回顾 第14讲 矩阵的奇异值分解 酉对角分解 一般矩阵的奇异值分解 Penrose广义逆
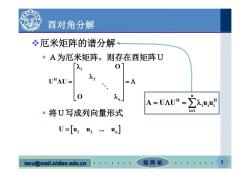
酉对角分解 冬厄米矩阵的谱分解 ·A为厄米矩阵,则存在酉矩阵U 0 UHAU- =Λ 0 A=UAUH=∑u ■将U写成列向量形式 U=[u1u2…u] lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 3 酉对角分解 厄米矩阵的谱分解 A为厄米矩阵,则存在酉矩阵U 将U写成列向量形式 1 H 2 n O U AU O U u u ... u 12 n n H H iii i 1 A U U uu

酉对角分解 冬非奇异矩阵的酉对角分解 ·定理 ·设A为n阶非奇异矩阵,则存在n阶酉矩阵U及V, 使得 01 0 62 U"AV= o,>0(i=1,2,,n) 0 6 A= i=1 ·若将U、V写成U=[u,u2…u],V=[y,v2…vn] lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 4 酉对角分解 非奇异矩阵的酉对角分解 定理 • 设A为n阶非奇异矩阵,则存在n阶酉矩阵U及V, 使得 • 若将U、V写成 H 1 2 n O U AV , . . O i 0(i 1, 2,..., n) U u u ... u , V v v ... v 12 n 12 n n H iii i 1 A uv

酉对角分解 冬酉对角分解的求法 ·先对AHA对角化(酉对角化) ■求出变换矩阵V ·再令U=AV∑ A=U∑VH lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 5 酉对角分解 酉对角分解的求法 先对AHA对角化(酉对角化) 求出变换矩阵V 再令 1 U AV H AU V

一 般矩阵的奇异值分解 定理:设A∈Cm知 ·则存在m阶酉矩阵U及n阶酉矩阵V,使 0 r行 UHAV= 0 0(m-r)行 6 r列 (n-r)列 62 A=U lexu@mail.xidian.edu.cn 矩阵论
lexu @mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 6 一般矩阵的奇异值分解 定理:设 则存在 m阶酉矩阵 U 及 n阶酉矩阵 V , 使 m n A C r 1 2 H r 0 O r U AV 0 O O (m r) r (n r) 行 行 列 列 1 2 H r O AU V . O O

o 01 V= [V I V] r列(n-r)列 VH(AHA)V= 0 令U1=AV∑ 冬由基扩充定理可知,可在U,的基础上构造酉 矩阵U=[UU2] lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 由基扩充定理可知,可在U1的基础上构造酉 矩阵U=[U1|U2] 7 2 1 2 2 H H 2 r n n O V (A A)V . O O V |V 1 2 V r (n r) 列 列

Penrose 广义逆 必何谓广义 ·即推广了原有概念或结果 逆矩阵一般概念 ·针对非奇异的(或称为满秩的)方阵 ·这一概念可推广到 ·奇异方阵 ·非方矩阵 ·事实上,Penrose)广义逆矩阵涵盖了两种情况 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 8 Penrose 广义逆 何谓广义 即推广了原有概念或结果 逆矩阵一般概念 针对非奇异的(或称为满秩的)方阵 这一概念可推广到 • 奇异方阵 • 非方矩阵 • 事实上, Penrose广义逆矩阵涵盖了两种情况

Penrose 广义逆 Penrose定义 .设A∈Cmxm,若Z∈Cxm且使如下四个等式成立 AZA=A,ZAZ=Z,(AZ)=AZ,(ZA)=ZA ·则称Z为A的Moore-Penrose(广义)逆 ·记为A+ ■上述四个等式又依次称为Penrose方程(i一iv) Moore-.Penrose逆的存在性和唯一性 ·定理:任给A∈Cmm,A*均存在且唯一 A=UDVH Z=VDUE lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 9 Penrose 广义逆 Penrose定义 则称Z为A的Moore-Penrose(广义)逆 记为A+ 上述四个等式又依次称为Penrose方程(i-iv) Moore-Penrose逆的存在性和唯一性 定理:

Penrose 广义逆 {,逆的定义 。HA∈CmⅫ,若Z∈Cxm ■且Z满足Penrose方程中的第(①),(),…,()个方程, 则称Z为A的,逆 ■记为Ai山 ■其全体记为A{i,j,,} ·共15类C4+C+C3+C4=15 ·常用如下5类 -A1},A{1,2,A{1,3},A{1,4},A{1,2,3,4} lexu@mail.xidian.edu.cn 矩阵论 。。-··。。10
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 10 Penrose 广义逆 {i,j,l}逆的定义 且Z满足Penrose方程中的第 个方程, 则称Z为A 的{i,j,l}逆 其全体记为 • 共15类 • 常用如下5类 – A{1}, A{1,2}, A{1,3}, A{1,4}, A{1,2,3,4} (i),(j), ,(l) A{i, j, ,l} 1234 C C C C 15 4444
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)14 矩阵的奇异值分解.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)13 QR分解及满秩分解.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)12 矩阵的QR分解.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2011)11 Penrose广义逆矩阵的定义及存在性.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)10 矩阵三角分解.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)09 矩阵函数及其微积分.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)08 矩阵函数的求解.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)07 Jordan标准形分析.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)06 Jordan标准形.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)05 矩阵对角化.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)04 线性变换矩阵及其对角化.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)03 直和及线性变换.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)02 线性空间及线性子空间.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)01 线性空间.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2017)第24讲 初等函数映射.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2017)第23讲 共形映射.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2017)第22讲 留数在积分中的应用及复习.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2017)第21讲 留数.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2011)第21讲 留数在积分中的应用及复习.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2017)第20讲 留数基础.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)16 Penrose广义逆与Moore广义逆.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)17 Penrose广义逆与Moore广义逆.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)18 广义逆的应用.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)19 最小二乘法.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)20 全面最小二乘法.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2015)21 范数理论.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2015)22 范数理论及特征值估计.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2015)23 广义特征值与极小极大原理.pdf
- 同济大学:工程硕士研究生教材《数值分析与矩阵论》书籍PDF电子版(工程数学,上册).pdf
- 高等学校研究生教材:《有限单元法》书籍PDF电子版 Finite Element Method(共十七章,编著:薛守义).pdf
- 高等学校教材:《近世代数》书籍PDF电子版(第二版,编著:杨子胥,共六章).pdf
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.1 消元法.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.2 n维向量空间.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.3 线性相关性.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.4 矩阵的秩.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.5 线性方程组有解判别定理.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.6 线性方程组解的结构.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第四章 矩阵 4.1 矩阵的概念.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第四章 矩阵 4.2 矩阵的运算.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第四章 矩阵 4.3 矩阵乘积的行列式与秩.pptx
