西安电子科技大学：《矩阵论》研究生课程教学课件（讲义，2014）02 线性空间及线性子空间

AN 矩阵论 主讲教师：徐乐 2014年9月24日星期三

矩阵论 主讲教师：徐乐 2014 年 9 月24日星期三

上讲回顾 冬第一讲线性空间 ■线性空间的定义及性质 ■线性空间的基 lexu@mail.xidian.edu.cn 矩阵论。·。。···

上讲回顾 第一讲 线性空间  线性空间的定义及性质  线性空间的基 lexu@mail.xidian.edu.cn 矩 阵 论 2

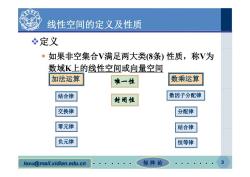
线性空间的定义及性质 必定义 ·如果非空集合V满足两大类(8条)性质，称V为 数域K上的线性空间或向量空间 加法运算 一性 数乘运算 结合律 封闭性 数因子分配律 交换律 分配律 零元律 结合律 负元律 恒等律 lexu@mail.xidian.edu.cn 矩阵论

线性空间的定义及性质 定义  如果非空集合 V满足两大类(8 条) 性质，称 V 为 数域 K上的线性空间 或向量空间 加法运算 唯一性 数乘运算 结合律 数因子分配律 封闭性 交换律 零元律 分配律 结合律 负元律 恒等律 lexu @mail.xidian.edu.cn 矩 阵 论 3

线性空间的基与坐标 基的定义 ■设V是数域K上的线性空间，x1,2,…,x(≥1) 是属于V的个任意元素，如果它满足 ·X1,七2，七线性无关； ·V中任一向量x均可由x,2,…,x线性表示 则称x1,x2,…,x为V的一个基 ■称x1,2,…,X为该基的基元素 lexu@mail.xidian.edu.cn 矩阵论

线性空间的基与 线性空间的基与 标坐 基的定义  设V是数域K上的线性空间， x1, x2 ,… , xr (r≥1) 是属于V的r个任意元素，如果它满足 • x1, x2 ,… , xr线性无关； • V中任 向量 一 x均可由x1, x2 ,… , xr线性表示  则称x1, x2 ,… , xr为V的一个基  称x1, x2 ,… , xr为该基的基元素 lexu@mail.xidian.edu.cn 矩 阵 论 4

第二讲线性空间及线性子空间 线性空间 冬坐标 基变换与坐标变换 冬线性子空间 冬定义及其性质 冬子空间的交与和 lexu@mail.xidian.edu.cn 矩阵论●

第 讲二 线性空间及线性子空间 线性空间 坐标 基变换与坐标变换 线性子空间 定义及其性质 子空间的交与和 lexu@mail.xidian.edu.cn 矩 阵 论 5

线性空间的坐标 坐标的定义 称线性空间V的一个基x1,x2…,x为V的一 个坐标系 xev"它在该基下的线性表示为： 含Geer=12m 气，5,5n为x在该坐标系中的坐标或分量 (5,52,5n) lexu@mail.xidian.edu.cn 矩阵论 6

线性空间的坐标  坐标的定义  称线性空间 V n的一个基x 1, x2 ,… , x n 为 V n的一 个坐标系  它在该基下的线性表示为： lexu @mail.xidian.edu.cn 矩 阵 论 6

线性空间的坐标 。一般来说，线性空间及其元素是抽象的对 象，不同空间的元素完全可以具有千差万 别的类别及性质 冬坐标表示却把它们统一了起来，坐标表示 把这种差别留给了基和基元素 由坐标所组成的新向量仅由数域中的数表 示出来 lexu@mail.xidian.edu.cn 矩阵论

线性空间的坐标 一般来说，线性空间及其元素是抽象的对 象，不同空间的元素完全可以具有千差万 别的类别及性质 坐标表示却把它们统 坐标表示却把它们统 了起来 一 ，坐标表示 把这种差别留给了基和基元素 由坐标所组成的新向量仅由数域中的数表 示出来 lexu @mail.xidian.edu.cn 矩 阵 论 7

线性空间的坐标 更进一步，原本抽象的“加法”及“数乘” 经过坐标表示就演化为向量加法及数对向 量的数乘 lexu@mail.xidian.edu.cn 矩阵论

线性空间的坐标 更进一步，原本抽象的“加法”及 “数乘” 经过坐标表示就演化为向量加法及数对向 量的数乘 lexu @mail.xidian.edu.cn 矩 阵 论 8

线性空间的坐标 x+y=(51X1+522++5mxn)+(711+72x2++7mm) =(51+71)心1+(52+72)心2+.+(5n+7m)x =5,5.5,）→x+y=(6+,5+,5+n.） y=(n1,72…,7n) lexu@mail.xidian.edu.cn 矩阵论●

线性空间的坐标 lexu @mail.xidian.edu.cn 矩 阵 论 9

线性空间的坐标 x=k(5x+52x2+…+5nxn)=(k5i)x+(k52)x2+…+(k5n)xm →(k5,k52…,k5n) x=(5,52,5n)→=(k51,k52,k53) lexu@mail.xidian.edu.cn 矩阵论 10

线性空间的坐标 11 2 2 1 1 2 2 ( )( ) ( ) ( ) nn n n kx k x x x k x k x k x              ( , , ) 1 2 n  k k  k lexu@mail.xidian.edu.cn 矩 阵 论 10