西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)14 矩阵的奇异值分解

131 UNIVE 矩阵论 主讲教师:徐乐 2014年12月10日星期三
2014年12月10日星期三 矩 阵 论 主讲教师:徐乐

不红 上讲回顾 第13讲QR分解及满秩分解 ·矩阵QR分解计算方法 ·矩阵的满秩分解 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 2 上讲回顾 第13讲 QR分解及满秩分解 矩阵QR分解计算方法 矩阵的满秩分解

QR分解 冬求QR分解的方法 ·方法一l采用Givens,方法 ■方法二]采用Householde方法 ·[方法三]Gram-schmidt正交归一化方法 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 3 QR分解 求QR分解的方法 [方法一]采用Givens方法 [方法二]采用Householde方法 [方法三] Gram-schmidt正交归一化方法

矩阵的满秩分解 冬定义 E∈Cmxr,G1 ECrxn ■设A∈Cmx"(r>0) =FGL ·若存在矩阵F∈CIXr G∈Crx =(FD)(D-G) ·使得A=FG =F(DD-)G ·称其为A的一个满秩分解 A=FG ■Note: ·F为列满秩矩阵,即列数等于秩 VD∈Crw ·G为行满秩矩阵,即行数等于秩 任何非零矩阵均 ·满秩分解不唯一 可逆方阵 存在满秩矩阵 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 4 矩阵的满秩分解 定义 设 • 若存在矩阵 • 使得A=FG • 称其为A的一个满秩分解 Note: • F为列满秩矩阵,即列数等于秩 • G为行满秩矩阵,即行数等于秩 • 满秩分解不唯一 m n A C (r 0) r m r F Cr r n G Cr r r D Cr 可逆方阵 1 1 1 1 F G (FD)(D G) F(DD )G A FG mr rn F C ,G C 1r 1r 任何非零矩阵均 存在满秩矩阵

矩阵的满秩分解 定义:设A∈Cmx"(r>0) ·若存在矩阵F∈CIrG∈Cxn ■使得A=FG ·称其为A的一个满秩分解 Note: G ·满秩分解不唯一 =FG 0 冬存在性定理 ·任何非零矩阵均存在满秩矩阵 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 5 矩阵的满秩分解 定义:设 若存在矩阵 使得A=FG 称其为A的一个满秩分解 Note: 满秩分解不唯一 存在性定理 任何非零矩阵均存在满秩矩阵 m n A C (r 0) r m r F Cr r n G Cr . G A F . S .... FG . O

矩阵的满秩分解 Hermite标准形(行阶梯标准形) 00102 0001 3 a设B∈Cmx"(r>0) B 0000 0 ·且满足 00000s ·B的前行中每一行至少含一个非零元素(称为非零 行),且第一个非零元素为1,而后(m-r)行的元素 全为零(称为零行) ·若B中第i行的第一个非零元素(即1)在第j列 (1,2,),则j1<j2<.<j ·矩阵的第j1列,第j2列,,第,列合起来恰为m阶单 位方阵1m的前r列(即j1,j2,,j,列上除了前述的1外 全为0)则称为Hermite标准形 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 6 矩阵的满秩分解 Hermite标准形(行阶梯标准形) 设 且满足 • B的前r行中每一行至少含一个非零元素(称为非零 行),且第一个非零元素为1,而后(m-r)行的元素 全为零(称为零行) • 若B中第 i 行的第一个非零元素(即1)在第ji列 (i=1,2,…,r),则 j1 < j2 <…< jr • 矩阵的第j1列,第j2列,…,第jr列合起来恰为m阶单 位方阵Im的前r列(即j1 , j2 ,…, jr列上除了前述的1外 全为0)则称为Hermite标准形 m n B C (r 0) r 4 5 2 2 4 5 00102 00013 B C 00000 00000 j1 j2

矩阵的满秩分解 冬满秩分解的一种求法 A=FG ·设A∈Cmxm ·采用行初等变换将A化成Hermite标准形,其矩阵形 式为EA=B,其中B为Hermite标准形定义中给出 的形状 ·选取置换矩阵 一用P右乘任何矩阵(可乘性得到满足时),即可将该矩阵 的第j:列置换到新矩阵(即乘积矩阵)的第1列 令P=[BI] =[ee.…e,]neCw r列(n-r)列 ·令G=B的前r行∈Cr F=AP∈Cmx lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 7 矩阵的满秩分解 满秩分解的一种求法 设 • 采用行初等变换将A化成Hermite标准形,其矩阵形 式为EA=B,其中B为Hermite标准形定义中给出 的形状 • 选取置换矩阵 m n A Cr – 用P右乘任何矩阵(可乘性得到满足时),即可将该矩阵 的第ji列置换到新矩阵(即乘积矩阵)的第i列 – 令 • 令G=B的前r行 1 r (n r) P P |* 列 列 1 2r n r 1 j jj r n r P e e ...e C r n Cr m r F AP C 1 r A FG

第14讲矩阵的奇异值分解 冬酉对角分解 一般矩阵的奇异值分解 lexu@mail.xidian.edu.cn 矩阵论●
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 8 第14讲 矩阵的奇异值分解 酉对角分解 一般矩阵的奇异值分解
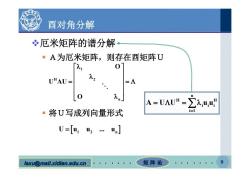
酉对角分解 冬厄米矩阵的谱分解 ·A为厄米矩阵,则存在酉矩阵U 0 UHAU= =Λ 0 入 A=UAUH-∑uu ·将U写成列向量形式 i-l U=[u1u2…u.] lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 9 酉对角分解 厄米矩阵的谱分解 A为厄米矩阵,则存在酉矩阵U 将U写成列向量形式 1 H 2 n O U AU O U u u ... u 12 n n H H iii i 1 A U U uu

酉对角分解 冬非奇异矩阵的酉对角分解 。定理 ·设A为n阶非奇异矩阵,则存在n阶酉矩阵U及V, 使得 01 0 62 U"AV= o,>0(i=1,2,,n) uV 0 i=1 ·若将U、V写成U=[u,u,…u],V=[y1v2… Vn. lexu@mail.xidian.edu.cn 矩阵论 10
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 10 酉对角分解 非奇异矩阵的酉对角分解 定理 • 设A为n阶非奇异矩阵,则存在n阶酉矩阵U及V, 使得 • 若将U、V写成 H 1 2 n O U AV , . . O i 0(i 1, 2,..., n) U u u ... u , V v v ... v 12 n 12 n n H iii i 1 A uv
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)13 QR分解及满秩分解.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)12 矩阵的QR分解.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2011)11 Penrose广义逆矩阵的定义及存在性.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)10 矩阵三角分解.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)09 矩阵函数及其微积分.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)08 矩阵函数的求解.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)07 Jordan标准形分析.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)06 Jordan标准形.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)05 矩阵对角化.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)04 线性变换矩阵及其对角化.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)03 直和及线性变换.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)02 线性空间及线性子空间.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)01 线性空间.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2017)第24讲 初等函数映射.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2017)第23讲 共形映射.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2017)第22讲 留数在积分中的应用及复习.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2017)第21讲 留数.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2011)第21讲 留数在积分中的应用及复习.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2017)第20讲 留数基础.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2011)第20讲 留数.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)15 Penrose广义逆的性质.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)16 Penrose广义逆与Moore广义逆.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)17 Penrose广义逆与Moore广义逆.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)18 广义逆的应用.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)19 最小二乘法.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)20 全面最小二乘法.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2015)21 范数理论.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2015)22 范数理论及特征值估计.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2015)23 广义特征值与极小极大原理.pdf
- 同济大学:工程硕士研究生教材《数值分析与矩阵论》书籍PDF电子版(工程数学,上册).pdf
- 高等学校研究生教材:《有限单元法》书籍PDF电子版 Finite Element Method(共十七章,编著:薛守义).pdf
- 高等学校教材:《近世代数》书籍PDF电子版(第二版,编著:杨子胥,共六章).pdf
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.1 消元法.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.2 n维向量空间.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.3 线性相关性.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.4 矩阵的秩.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.5 线性方程组有解判别定理.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.6 线性方程组解的结构.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第四章 矩阵 4.1 矩阵的概念.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第四章 矩阵 4.2 矩阵的运算.pptx
