西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)08 矩阵函数的求解

UNIVE 矩阵论 主讲教师:徐乐 2014年12月10日星期三
2014年12月10日星期三 矩 阵 论 主讲教师:徐乐

上讲回顾 第8讲Jordan标准形应用 ·Jordan标准形的幂及多项式 ·矩阵序列 ·矩阵级数 ·方阵的幂级数 ·矩阵函数 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 2 上讲回顾 第8讲 Jordan标准形应用 Jordan标准形的幂及多项式 矩阵序列 矩阵级数 方阵的幂级数 矩阵函数

Jordan标准形的幂及多项式 冬Jordan标准形的幂 J 亦为类似上三 J 角形条带矩阵 •在与主对角线 平行的斜线上各 元素相等 「 22 1 0 2 2 1 J= 2 21 0 lexu@mail.xidian.edu.cn 矩阵论
lexu @mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 3 Jordan标准形的幂及多项式 Jordan标准形的幂 k s k k k J J J J 2 1 i i i Ji 0 1 1 0 2 2 2 2 2 2 0 2 1 2 2 1 2 1 0 i i i i i i i i i Ji •ji k亦为类似上三 角形条带矩阵 •在与主对角线 平行的斜线上各 元素相等 t t Ck i

Jordan标准形的幂及多项式 Jordan标准形多项式 f(x)-agx-d+ajx+..+am" -0 1 0 0 22: 1 0 2 fJ,)=a -a +a +。 1 22 10 0 0 f)f'(2) 1 (0m:-1): 1 f(A) f'(a) fm-2() (m,-2)! f'() f(A) lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 4 Jordan标准形的幂及多项式 Jordan标准形多项式 0 1 0 ( ) ... m k m k m k f x ax a ax a x

矩阵序列 冬矩阵序列 ▣定义 ·设有矩阵序列{4}.其中4=(a) .且当k→o时)→a ·称{4}收敛 ·把A=(a)叫做{A}的极限 或称{4}收敛于A IimA)=A或A)→A k->oc k→0 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 5 矩阵序列 矩阵序列 定义 • • • • •
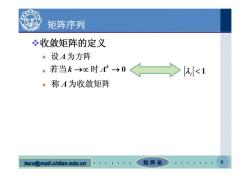
矩阵序列 冬收敛矩阵的定义 ·设A为方阵 .若当kx时A→0<>2,<1 ·称A为收敛矩阵 lexu@mail.xidian.edu.cn 矩阵论一
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 6 矩阵序列 收敛矩阵的定义

矩阵级数 必定义 ·矩阵序列{4}的无穷和4四+4+…++… 4 记为 k=1 矩阵级数 ·部分和S-2种 ■若矩阵序列{S收敛,且有极限S,则称该矩阵 级数收敛,且有和S,记为S=∑A ·不收敛的矩阵级数称为是发散的 lexu@mail.xidian.edu.cn 矩阵论雪
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 7 矩阵级数 定义 部分和 若矩阵序列{S(N)}收敛,且有极限S, 则称该矩阵 级数收敛,且有和S,记为 矩阵级数 1 ( ) k k A 记为 ( ) () 1 N N k k S A

方阵的幂级数 冬定义 ·A为方阵 ·∑4,(4°=D称为1的幂级数 =0 ·∑A称为A的Neumann级数 [定理]Neumann级数收敛的充要条件是 -A为收敛矩阵 -且在收敛时其和为(I-A)1 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 8 方阵的幂级数 定义 A为方阵 称为A的Neumann级数 • [定理] Neumann级数收敛的充要条件是 – A为收敛矩阵 – 且在收敛时其和为 (I - A)-1

方阵的幂级数 必收敛圆 e)- ·若矩阵A的特征值全部落在幂级数的收敛圆内 则矩阵幂级数是绝对收敛的A)=∑c4,(4P=I ·反之,若A存在落在的收敛圆(z)外的特征值,则 A)是发散的 必[推论创 ·若幂级数在整个复平面上收敛,则对任何的方阵 A,(A)均收敛 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 9 方阵的幂级数 收敛圆 若矩阵A的特征值全部落在幂级数的收敛圆内 则矩阵幂级数是绝对收敛的 反之, 若A存在落在的收敛圆φ(z)外的特征值, 则 φ(A)是发散的 [推论] 若幂级数在整个复平面上收敛, 则对任何的方阵 A, φ(A)均收敛 0 ( ) k k k z c z 0 0 ( ) ,( ) k k k A cA A I

矩阵函数 定义 ·以矩阵为自变量的“函数”(实际上是“函矩阵”) A si血(40=分_-1) (2n+1):1 os(A0=月-1 (2n)H lexu@mail.xidian.edu.cn 矩阵论● 。。··。。。10
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 10 矩阵函数 定义 以矩阵为自变量的“函数”(实际上是“函矩阵”)
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)07 Jordan标准形分析.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)06 Jordan标准形.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)05 矩阵对角化.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)04 线性变换矩阵及其对角化.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)03 直和及线性变换.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)02 线性空间及线性子空间.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)01 线性空间.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2017)第24讲 初等函数映射.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2017)第23讲 共形映射.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2017)第22讲 留数在积分中的应用及复习.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2017)第21讲 留数.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2011)第21讲 留数在积分中的应用及复习.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2017)第20讲 留数基础.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2011)第20讲 留数.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2017)第19讲 洛朗级数.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2011)第19讲 留数基础.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2016)第18讲 幂级数及泰勒级数.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2011)第18讲 洛朗级数.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2016)第17讲 复数项级数.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2016)第16讲 复数与复变函数.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)09 矩阵函数及其微积分.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)10 矩阵三角分解.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2011)11 Penrose广义逆矩阵的定义及存在性.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)12 矩阵的QR分解.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)13 QR分解及满秩分解.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)14 矩阵的奇异值分解.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)15 Penrose广义逆的性质.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)16 Penrose广义逆与Moore广义逆.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)17 Penrose广义逆与Moore广义逆.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)18 广义逆的应用.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)19 最小二乘法.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2014)20 全面最小二乘法.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2015)21 范数理论.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2015)22 范数理论及特征值估计.pdf
- 西安电子科技大学:《矩阵论》研究生课程教学课件(讲义,2015)23 广义特征值与极小极大原理.pdf
- 同济大学:工程硕士研究生教材《数值分析与矩阵论》书籍PDF电子版(工程数学,上册).pdf
- 高等学校研究生教材:《有限单元法》书籍PDF电子版 Finite Element Method(共十七章,编著:薛守义).pdf
- 高等学校教材:《近世代数》书籍PDF电子版(第二版,编著:杨子胥,共六章).pdf
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.1 消元法.pptx
- 西安电子科技大学:《高等代数》课程PPT教学课件(讲稿)第三章 线性方程组 3.2 n维向量空间.pptx
