重庆医科大学：《医学统计学》课程教学资源（试卷习题）医学统计学套题6（答案）

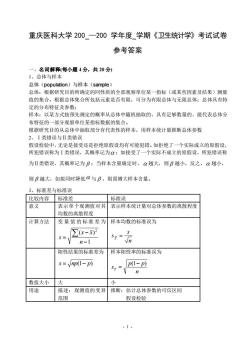
重庆医科大学200一200学年度学期《卫生统计学》考试试卷 参考答案 一、名词解释（每小题4分，共20分） 1、总体与样本 总体(population)与样本(sample) 总体：根据研究目的所确定的同性质的全部观察单位某一指标（或某些因素及结果）测量 值的集合。根据总体集合所包括元素是否有限，可分为有限总体与无限总体：总体具有特 定的分布特征及参数： 样本：以某方式按预先规定的概率从总体中随机抽取的、具有足够数量的、能代表总体分 布特征的一部分观察单位某指标数据的集合。 根据研究目的从总体中抽取部分有代表性的样本，用样本统计量推断总体参数 2、1类错误与Ⅱ类错误 假设检验中，无论是接受还是拒绝原假设均有可能犯错。如拒绝了一个实际成立的原假设， 所犯错误称为I类错误，其概率记为α：如接受了一个实际不成立的原假设，所犯错误称 为Ⅱ类错误，其概率记为B:当样本含量确定时，α越大，则B越小，反之，α越小， 则B越大，如拟同时降低与B,则需增大样本含量。 3、标准差与标准误 比较内容标准差 标准误 意义 表示单个观测值对其 表示样本统计量对总体参数的离散程度 均数的离散程度 计算方法 变量值的标准差为样本均数的标准误为 ∑x-列 8= n-l 阳性结果的标准差为 样本阳性率的标准误为 s=np(1-p) 数值大小 大 小 用途 描述：观测值的变异推断：估计总体参数的可信区间 范围 假设检验 1-

- 1 - 重庆医科大学 200 —200 学年度 学期《卫生统计学》考试试卷 参考答案 一、名词解释(每小题 4 分，共 20 分) 1、总体与样本 总体（popullatiion）与样本（samplle） 总体：根据研究目的所确定的同性质的全部观察单位某一指标（或某些因素及结果）测量 值的集合。根据总体集合所包括元素是否有限，可分为有限总体与无限总体；总体具有特 定的分布特征及参数； 样本：以某方式按预先规定的概率从总体中随机抽取的、具有足够数量的、能代表总体分 布特征的一部分观察单位某指标数据的集合。 根据研究目的从总体中抽取部分有代表性的样本，用样本统计量推断总体参数 2、Ⅰ类错误与Ⅱ类错误 假设检验中，无论是接受还是拒绝原假设均有可能犯错。如拒绝了一个实际成立的原假设， 所犯错误称为Ⅰ类错误，其概率记为  ；如接受了一个实际不成立的原假设，所犯错误称 为Ⅱ类错误，其概率记为  ；当样本含量确定时，  越大，则  越小，反之，  越小， 则  越大，如拟同时降低  与  ，则需增大样本含量。 3、标准差与标准误 比较内容 标准差 标准误 意义 表示单个观测值对其 均数的离散程度 表示样本统计量对总体参数的离散程度 计算方法 变 量 值 的 标准 差 为 1 ( ) 2 − − =  n x x s 样本均数的标准误为 n s s X = 阳性结果的标准差为 s = np(1− p) 样本阳性率的标准误为 n p p sP (1− ) = 数值大小 大 小 用途 描述：观测值的变异 范围 推断：估计总体参数的可信区间 假设检验

4.X±1.96S与X±1.96S X±1.96S:从正态总体中抽样，样本含量较大时，观测值95%的波动范围： X±1.96S:从正态总体中抽样，样本含量较大时，总体均数95%的可信区间（置信区间）》 5、直线相关与直线回归 1)区别 资料要求。 回归要求因变量Y在给定x=x0的条件下，服从正态分布；X是可以精确测量和严格 控制的变量，一般称为I型回归。相关要求两个变量X、Y服从双变量正态分布。这种资 料若进行回归分析称为Ⅱ型回归。可以计算两个回归方程： 应用： 相关分析主要是描述两个变量之间线性关系的密切程度和方向：回归分析说明两变量 间依存变化的数量关系，不仅可以揭示变量x对变量y的影响大小，还可以由回归方程 进行预测和控制 统计量： 回归分析中主要统计量为截距a和回归系数b,相关分析统计量为相关系数r。回归系 数有单位，相关系数无单位， 2)联系 r与b符号一致 对一组数据若同时计算r与b,它们的正负号是一致的。 假设检验等价 对同一样本，r和b的假设检验得到的1值相等。· 3)用回归解释相关 的平方称为决定系数，r2= SSa归 SS 二、单项选择题（从每小题的五个备选答案中，选出一个正确的答案，并将其字母填在题 干横线上，每小题2分，共30分) 2B 3B 6.E7.E8.B9.E10.D 11.C12.D13.E 14.B15D 三、填空题（每空1分，共20分） 1、构成比、相对比、率 2、参数估计、假设检验 3、科研设计、资料收集、资料整理、资料分析 4、计数、计量、等级 .2-

- 2 - 4. X ±1.96S 与 X ±1.96 x S X ±1.96S：从正态总体中抽样，样本含量较大时，观测值 95%的波动范围； X ±1.96 x S ：从正态总体中抽样，样本含量较大时，总体均数 95%的可信区间（置信区间） 5、直线相关与直线回归 1）区别 资料要求: 回归要求因变量 Y 在给定 x=x0 的条件下，服从正态分布; X 是可以精确测量和严格 控制的变量，一般称为Ⅰ型回归。相关要求两个变量 X、Y 服从双变量正态分布。这种资 料若进行回归分析称为Ⅱ型回归。可以计算两个回归方程； 应用： 相关分析主要是描述两个变量之间线性关系的密切程度和方向；回归分析说明两变量 间依存变化的数量关系，不仅可以揭示变量 x 对变量 y 的影响大小，还可以由回归方程 进行预测和控制 统计量： 回归分析中主要统计量为截距 a 和回归系数 b，相关分析统计量为相关系数 r。回归系 数有单位,相关系数无单位。 2）联系 r 与 b 符号一致 对一组数据若同时计算 r 与 b，它们的正负号是一致的。 假设检验等价 对同一样本，r 和 b 的假设检验得到的 t 值相等。• 3）.用回归解释相关 r 的平方称为决定系数， 总 回归 SS SS r = 2 二、单项选择题 (从每小题的五个备选答案中，选出一个正确的答案，并将其字母填在题 干横线上，每小题 2 分，共 30 分) 1.A 2.B 3.B 4.C 5.C 6.E 7.E 8.B 9.E 10.D 11.C 12.D 13.E 14.B 15.D 三、填空题 (每空 1 分，共 20 分) 1、构成比、相对比、率 2、参数估计、假设检验 3、科研设计、资料收集、资料整理、资料分析 4、计数、计量、等级

5、对照原则、随机原则、重复原则 6、处理因素、受试对象、效应指标 7、反证法和根据“小概率事件在一次试验中几乎不会发生的原理，用概率的思想决定是 否拒绝原假设。 四、应用题（第1题4分，第2题8分，第3题8分，第4题10分，共30分） 1、此结论不正确。因为该资料用构成比代替率进行判断。应用工人、农民、学生、干部 及其他这几部分各自的沙眼患病率来比较。 2、 (1)计数资料 (2)配对设计 (3)配对资料的chi-square test。在此例中由于b+c=26(40,故应用其矫正公式。 自由度：1 (4)假设：H0:两种剂量的毒性无差别 H1:两种剂量的毒性有差别 检验水准：a=0.05 (5)如果P>0.05:不拒绝H0,即现在所拥有的资料还不能说明两种剂量的毒性有差别。 如果P≤0.05：拒绝H0,接受H1,差别有统计学意义，可认为两种剂量的毒性不同。 3、 (1)计量资料 (2)组内配对设计方案，组间为完全随机设计。 (3)采用完全随机设计的t检验， 1=4-d Sa-a2 d:新药组治疗前后舒张压差值：d2：旧药组治疗前后舒张压差值： 正态分布的计量资料，方差齐。 (1)分别做该地健康7岁男女儿童频数表，可用算术均数、中位数描述集中趋势：用极 差、四分位数间距，方差、标准差描述离散趋势。 (2)分别制定男女95%的身高参考值范围。计算健康7岁男女儿童身高均数的可信区间。 (3)两独立样本的t检验，分析该地健康7岁男女儿童身高是否相同。 3-

- 3 - 5、对照原则、随机原则、重复原则 6、处理因素、受试对象、效应指标 7、反证法和根据“小概率事件在一次试验中几乎不会发生的原理，用概率的思想决定是 否拒绝原假设。 四、应用题（第 1 题 4 分，第 2 题 8 分，第 3 题 8 分，第 4 题 10 分，共 30 分） 1、此结论不正确。因为该资料用构成比代替率进行判断。应用工人、农民、学生、干部 及其他这几部分各自的沙眼患病率来比较。 2、 （1）计数资料 （2）配对设计 （3）配对资料的 chi-square test。在此例中由于 b+c=26〈40，故应用其矫正公式。 自由度：1 （4）假设：H0：两种剂量的毒性无差别 H1：两种剂量的毒性有差别 检验水准：a=0.05 （5）如果 P>0.05：不拒绝 H0，即现在所拥有的资料还不能说明两种剂量的毒性有差别。 如果 P≤0.05：拒绝 H0，接受 H1，差别有统计学意义，可认为两种剂量的毒性不同。 3、 （1）计量资料 （2）组内配对设计方案，组间为完全随机设计。 （3）采用完全随机设计的 t 检验， 1 2 1 2 d d S d d t − − = 1 d ：新药组治疗前后舒张压差值； 2 d ：旧药组治疗前后舒张压差值； 4、 正态分布的计量资料，方差齐。 （1）分别做该地健康 7 岁男女儿童频数表，可用算术均数、中位数描述集中趋势；用极 差、四分位数间距，方差、标准差描述离散趋势。 （2）分别制定男女 95%的身高参考值范围。计算健康 7 岁男女儿童身高均数的可信区间。 （3）两独立样本的 t 检验，分析该地健康 7 岁男女儿童身高是否相同