吉林大学：《高等数学》课程电子教案（PPT课件）第一章 函数、极限、连续 §8 函数的连续性与间断点

第一—章 §8盈教的连疾性与间断点 函数连续性的定义 二、 函数的间断点 HIGH EDUCATION PRESS 机动目录上页下页返回结束

二、 函数的间断点 一、 函数连续性的定义 机动 目录 上页 下页 返回 结束 §8函数的连续性与间断点 第一章

函数连续性的定义 自然界有许多现象，如气温的变化，江河的水流，植 物的生长等等，都是连续地变化着的这种现象反映在函 数上，就是函数的连续性.例如就气温的变化来看，当时 间变动很微小时，气温的变化也很微小，这种特点就是 所谓的连续性 为了更好的刻画连续性，我们先引出增量的概念 设变量从它的一个初值u变到终值u2,终值与初值的 差u1~2就叫做变量的增量，记作△4，即 △u=142-41 1、增量△可以是正的，也可以是负的 2、记号△讲不表示某个量△与变量的乘积，而是一 个整体不可分割的记号 HIGH EDUCATION PRESS 00 机动目录上页下页 返[ 结

一、 函数连续性的定义 机动 目录 上页 下页 返回 结束 自然界有许多现象，如气温的变化，江河的水流，植 物的生长等等，都是连续地变化着的.这种现象反映在函 数上，就是函数的连续性.例如就气温的变化来看，当时 间变动很微小时，气温的变化也很微小，这种特点就是 所谓的连续性. 为了更好的刻画连续性，我们先引出增量的概念. 设变量u从它的一个初值u1变到终值u2，终值与初值的 差u1 - u2就叫做变量u的增量，记作 u, 即 2 1  = − u u u . 2、记号 1、增量 u 可以是正的，也可以是负的. u 并不表示某个量△与变量u的乘积，而是一 个整体不可分割的记号

定义1设函数y=f(x)在x的某邻域内有定义 如果limf(x)存在，且l1imf(x)=f(xo), 则称函数 X-X0 f(x)在x连续 可见，函数f(x)在点x,连续必须具备下列条件 (I)f(x)在点xo有定义，即f(xo)存在； (2) 极限limf(x)存在； x→x0 3 lim f(x)=f(xo). x→x0 连续函数的图形是一条连续而不间断的曲线 HIGH EDUCATION PRESS 机动目录上页下页返回结束

可见 , 函数 在点 0 x 定义1 在 的某邻域内有定义 , 则称函数 ( ) . f x 在x0 连续 (1) 在点 即 (2) 极限 (3) 设函数 连续必须具备下列条件: 存在 ; 且 有定义 , 存在 ; 机动 目录 上页 下页 返回 结束 如果 0 lim ( ) x x f x → 存在， (4) 连续函数的图形是一条连续而不间断的曲线

若f(x)在某区间上每一点都连续，则称它在该区间上 连续，或称它为该区间上的连续函数 在闭区间[a,b]上的连续函数的集合记作C[a,b] 例如，P(x)=ao+a41x+…+anx” 有理整函数) 在(-0，十0)上连续 又如，有理分式函数R(x)= P(x) Q(x) 在其定义域内连续 只要Q(xo)≠0，都有1imR(x)=R(xo) x→x0 HIGH EDUCATION PRESS 机动目录上页下页返回结束

( , ), lim ( ) ( ) continue 0 0 0 x P x P x x x   − +  = → 若 在某区间上每一点都连续 , 则称它在该区间上 连续 , 或称它为该区间上的连续函数 . C[a, b]. 例如, 在 上连续 . ( 有理整函数 ) 又如, 有理分式函数 在其定义域内连续. 在闭区间 上的连续函数的集合记作 只要 ( ) 0, Q x0  都有 lim ( ) ( ) 0 0 R x R x x x = → 机动 目录 上页 下页 返回 结束

对自变量的增量△x=x-x0,有函数的增量 △y=f(x)-f(xo)=f(x0+△x)-f(xo) 函数f(x)在点x,连续有下列等价命题 lim f(x)=f(xo) limf(xo+△x)=f(xo) x-→X0 Ax->0 lim△y=0 yy=f(x △x-→0 f(xo )f(xo)=f(xo") △x 左连续 右连续 Xx Vε>0,38>0，当x-=Ax<8时，有 f(x)-f(x=△yKe HIGH EDUCATION PRESS 机动目录上页下页返回结束

对自变量的增量 有函数的增量 y = f (x) o x y 0 x x x y lim ( ) ( ) 0 0 f x f x x x = → lim ( ) ( ) 0 0 0 f x x f x x +  =  → lim 0 0  =  → y x ( ) ( ) ( ) 0 0 0 − + f x = f x = f x 左连续 右连续   0,   0, 当 x − x0 = x   时, 有 f (x) − f (x ) = y   0 函数 在点 连续有下列等价命题: 机动 目录 上页 下页 返回 结束

例.证明函数y=sinx在(-o,+oo)内连续 证：x∈(-0，+∞) Ay=sin(x+Ax)-sinx =2sin cos(x+) Ay=2 sin cos(x+) ≤21=AxAx→0 即 lim.△y=0 △x→0 这说明y=sinx在(-o,+oo)内连续 同样可证：函数y=C0Sx在(-0，十0)内连续 HIGH EDUCATION PRESS 机动目录上页下页返回结束

例. 证明函数 在 内连续 . 证: x(−, + ) y = sin(x + x) −sin x 2 sin cos( ) 2 2 x x y x    = + = x x → 0 即 这说明 在 内连续 . 同样可证: 函数 在 内连续 . 0 机动 目录 上页 下页 返回 结束

二、 函数的间断点 设f(x)在点x,的某去心邻域内有定义，则下列情形 之一函数f(x)在点x,不连续 (1)函数f(x)在x,无定义； (2)函数f(x)在x,虽有定义，但1mf(x)不存在 x→X0 (3)函数f(x)在x,虽有定义，且1mf(x)存在，但 x今X0 limf(x)≠f(xo） x→X0 这样的点x。称为间断点 HIGH EDUCATION PRESS 机动目录上页下页返回结束

在 在 二、 函数的间断点 (1) 函数 (2) 函数 不存在; (3) 函数 存在 , 但 lim ( ) ( ) 0 0 f x f x x x  → 不连续 : 设 在点 的某去心邻域内有定义 , 则下列情形 这样的点 之一函数 f (x) 在点 虽有定义 , 但 虽有定义 , 且 称为间断点 . 在 无定义 ; 机动 目录 上页 下页 返回 结束

间断点分类： 第一类间断点： f(x。)及f(x,)均存在 若f(x,)=f(x,),称xo为可去间断点 若f(x,)≠f(x,),称x,为跳跃间断点 第二类间断点： f(x。)及f(x,)中至少一个不存在 若其中有一个为0，称x,为无穷间断点 若其中有一个为振荡，称x。为振荡间断点 HIGH EDUCATION PRESS 机动目录上页下页返回结束

间断点分类: 第一类间断点: 及 均存在 , 若 称 0 x 若 称 0 x 第二类间断点: 及 中至少一个不存在 , 称 0 x 若其中有一个为振荡 , 称 0 x 若其中有一个为 , 为可去间断点 . 为跳跃间断点 . 为无穷间断点 . 为振荡间断点 . 机动 目录 上页 下页 返回 结束

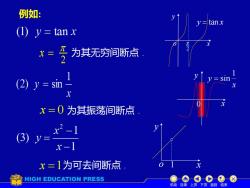
例如： =tanx (1)y=tanx x= 为其无穷间断点 1 (2)y sin 1y三 X x=0为其振荡间断点 x2-1 (3)y= x-1 x=1为可去间断点 HIGH EDUCATION PRESS 机动目录上页下页返回结束

2  x = 为其无穷间断点 . x = 0 为其振荡间断点 . x =1为可去间断点 . o x y 1 例如: y = tan x 2  x y o x y x y 1 = sin 0 机动 目录 上页 下页 返回 结束

x,x≠1 4y=={5,x=1 显然1imf(x)=1≠f() 112 x>1 X x=1为其可去间断点 x-1,x0 X f(0)=-1, f(0)=1 x=0为其跳跃间断点 HIGH EDUCATION PRESS 机动目录上页下页返回结束

1 lim ( ) 1 (1) 1 f x f x =  → 显然 x =1 为其可去间断点 .    =  = = , 1 , 1 ( ) 2 1 x x x (4) y f x o x y 2 1 1 (5)     +  = −  = = 1 , 0 0 , 0 1 , 0 ( ) x x x x x y f x x y o 1 −1 (0 ) = −1, − f (0 ) =1 + f x = 0 为其跳跃间断点 . 机动 目录 上页 下页 返回 结束